Dr. William Cassarly, Dr. Thomas Hough and Dr. Thomas Davenport, Optical Research Associates
Light pipes couple and shape light-source output distribution in a variety of illumination applications, including automotive and avionic displays, fiber optic illuminators and display backlights. Traditionally, successful design of these systems has required an educated selection of appropriate starting design, followed by time-consuming manual design iterations to optimize performance. An illumination system optimization algorithm now under development should reduce development time and deliver maximum energy transference to both circularly and noncircularly symmetric light pipe systems.
Angle-to-area converters
One important class of illumination light pipe systems is the “angle-to-area converter.” These optics convert flux of a given spatial and angular distribution to a different spatial and angular distribution. For maximum efficiency, angle-to-area conversion systems must preserve etendue, which means that the new angle and area are not freely chosen but rather dependent on each other and the input distribution. Practical issues, such as limited length, material losses and Fresnel surface reflections, often make it difficult to achieve maximum efficiency.
A simple example of this type of light pipe is an optic designed to transfer light from a rectangular input aperture to a rectangular output aperture of the same size but rotated by 90°. Shown are two design forms that can accomplish this (Figure 1). This case uses a 2 × 1-mm input aperture, a 1 × 2-mm output aperture, a 30° clipped lambertian input intensity distribution and a total system length of 10 mm.
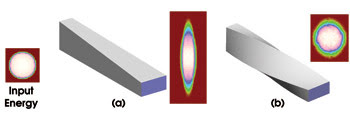
Figure 1. Comparing the input energy distribution after it has passed through a straight light pipe (a), and through a twisted light pipe (b), demonstrates that the output energy distribution (shown to the right of each design) of the twisted light pipe closely matches the input, indicating high-efficiency energy transfer.
The example is a hollow reflecting light pipe filled with air, but a solid version using total internal reflection could also be constructed. Because the input and output areas are identical, etendue preservation dictates that optimum efficiency will occur when the output distribution is identical to the input distribution. Therefore, the twisted light pipe clearly delivers higher-efficiency energy transfer.
A more difficult problem is a light pipe in which the output area is smaller than the input area, especially when total system length is constrained. Consider a system with a 2 × 1-mm input aperture and a 1 × 0.5-mm output aperture (with long axes oriented in the same direction), in which the shortest possible system length is desired.
In this case, efficiency improves when the light pipe sides are curved, rather than flat, as seen in the figure. However, no simple analytical methods can derive the optimum curve shapes because the length is predetermined. The traditional approach to this design problem is trial-and-error selection of curve shape and repeated system analysis until the efficiency appears to converge upon a maximum value. This method is time-consuming.
Optical Research Associates’ LightTools optimization routine solves this quickly and with a high degree of confidence. In this example, second-degree, rational Bezier curves specify the shapes of the curved sides. The optimization routine adjusts the positions of the curves’ central control points and their weighting factors to achieve maximum output energy. The result is an increase in efficiency from 87 percent (straight sides) to 95 percent (optimized, Bezier-controlled sides) for a constrained length of 2.6 mm.
Adding ‘wiggles’
The LightTools optimizer also enables the designer to explore many potential solutions, such as exotic geometries, with minimal time investment (Figure 2). This capability is highlighted in the case of a 4:1 rectangular-to-square converter with a 2 × 1-mm input aperture, a 0.71 × 0.71-mm output aperture and a length of 10 mm.
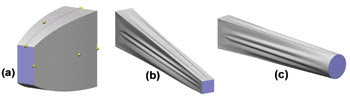
Figure 2. Software allows the designer to explore exotic geometries, such as a rectangular-to-rectangular light pipe with curved sides (a), a rectangular-to-square light pipe with “wiggles” (b) and a rectangular-to-circular light pipe with wiggles (c).
A straight light pipe delivers 78 percent efficiency, and a twisted solution, 80 percent. Adding “wiggles” to the straight light pipe can improve efficiency, but there is no obvious way to simultaneously optimize wiggle period and amplitude by hand.
The optimizer can vary wiggle parameters while holding all other components of the model constant. The best solution obtained, reached after just a few minutes of optimization time, has 20 wiggles with an amplitude of 0.0575 mm. The resulting efficiency is 91 percent — a substantial improvement over either of the other approaches.
The final example is a 1:1 area converter with a 2 × 1-mm rectangular input aperture and a 1.6-mm-diameter circular exit aperture. Because the areas are equal, the best energy transfer again occurs when the exiting angular distribution is identical to the input intensity distribution.
The three cases analyzed were a straight connection, a 90° twisted connection and a straight connection with a sinusoidal wiggle. In this instance, the straight solution yields efficiencies from 84 to 89 percent over lengths of about 10 to 100 mm. The twisted shape performs just slightly worse than this.
The addition of wiggles again improves the situation. Specifically, the optimizer determines that 16 wiggles, with amplitude of 0.05 mm, increase efficiency by about 8 percent for light pipes in the 20- to 100-mm- length range.
As a final note, the performance improvements delivered by the optimizer become more pronounced when the model includes real-world factors, such as light pipe reflectivity of less than 100 percent.
Meet the authors
William Cassarly is principal illumination engineer, Thomas Hough is director of illumination engineering, and Thomas Davenport is senior illumination engineer, all at Optical Research Associates in Tucson, Ariz.; e-mail: [email protected].