The generation of 1.6-fs pulses opens the way to a new regime of nonlinear optics and coherent control.
Dr. Miroslav Y. Shverdin, Dr. David R. Walker, Sunil N. Goda, G.Y. Yin and Stephen E. Harris, Stanford University, and Dr. Deniz D. Yavuz, University of Wisconsin
From Fourier theory, we know that any periodic shape may be formed by combining sinusoidal waves with prescribed amplitudes, frequencies and relative phases. Functions such as a square or sawtooth wave require frequencies covering several octaves of bandwidth.
In the acoustic regime, multioctave radiation sources are abundant. A typical concert piano spans seven octaves of bandwidth. The voice of a good opera singer can stretch over nearly four octaves.
In optics, a laser is a source of coherent, intense, monochromatic radiation, with a sinusoidal electric field. Over the past several years, our group has developed a unique source of laser radiation that spans more than four octaves of bandwidth — from 195 nm to 3 μm — and that consists of more than 200 discrete frequency components.
In our latest pulse-shaping experiments with this source, we achieved phase control over seven spectral components stretching from 410 nm to 1.56 μm, or two octaves. By changing the relative phases of these seven sidebands, we have synthesized a train of 1.6-fs pulses with a period of 11 fs. These pulses are single-cycle, consisting of one electric field oscillation under the envelope. We also have synthesized a frequency-modulated pulse, wherein the electric field chirp is apparent over three field oscillations.
Ultrashort pulse generation requires a wide-bandwidth coherent spectrum. An incoherent radiation source — such as sunlight, a high-pressure arc lamp or an atomic line emission lamp — consists of many spectral components, all with randomly varying phases. The time structure from such a source is white noise. In contrast, a coherent light source has a fixed phase relation among the spectral components, which interfere to produce well-defined waveforms.
Molecular modulation
It is well-known that an electro-optic modulator can phase-modulate an applied laser field to produce sidebands at new frequencies. These modulators, based on electro-optic crystals, have low conversion efficiencies and typical bandwidths of approximately 1 GHz. We have developed a process using molecular modulation that has unity conversion efficiency and a modulation bandwidth of 90 THz.1
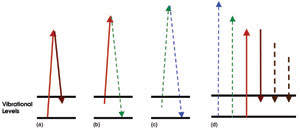
Figure 1. (a) The pump (red) and Stokes (dark red) driving lasers drive a molecular vibrational transition slightly off-resonance. (b) The pump laser mixes with the molecular vibration to generate an additional anti-Stokes frequency (broken green line). (c) The anti-Stokes field mixes with the molecular vibration to generate the next anti-Stokes frequency (broken blue line). (d) This process continues to generate both Stokes (broken lines to the left of solid lines) and anti-Stokes (broken lines to the right of solid lines) frequencies. The number of new frequencies depends on the efficiency of the process.
This method involves exciting a vibrational or a rotational mode of a molecule using two intense laser fields (Figure 1). Classically, we can picture this interaction as driving a harmonic oscillator near its resonance at the beat note frequency of the two lasers. In this manner, we prepare a very efficient molecular modulator. The resulting molecular motion mixes with the two applied fields to produce new coherent frequencies.
If many electro-optic modulators with different modulation frequencies are cascaded in series, the total number of produced sidebands will be the product of the number of sidebands that each modulator alone would produce. To produce more than 200 sidebands, we simultaneously excite a vibrational transition in D2 and a rotational transition in H2 using two pairs of lasers.

Figure 2. Three spectra demonstrate the effect of cascading the electro-optic modulators. The first is obtained by driving a vibrational transition in D2 (top). Driving a rotational transition in H2 produces the second (middle). The third is generated by simultaneously driving both transitions (bottom).
The experimental realization of this effect is shown in Figure 2. When we excite a fundamental vibrational transition in deuterium, we generate an additional 14 sidebands.1 When we excite a single rotational transition in hydrogen, we produce in excess of 27.2 If we simultaneously drive both transitions, we obtain the multiplicative spectrum.3
We can picture this process as cascading a vibrational and a rotational modulator. Here, the total number of observed frequencies is approximately one-half the product of the rotational and vibrational number of sidebands. This happens because the additional sidebands are generated at such low efficiency that they are not resolved.
Because of the experimental difficulties in simultaneously controlling the phases of so many sidebands, we used a single vibrational modulator in our pulse-shaping experiment. The vibrational spectrum was obtained by applying two Q-switched lasers: a diode-seeded Nd:YAG at 1064 nm with a pulse energy of 70 mJ and a pulse duration of 10 ns, and a homemade Ti:sapphire ring-cavity laser at 807 nm that produced transform-limited 15-ns pulses of 60 mJ. The Ti:sapphire was seeded by a tunable diode laser and pumped by the second harmonic of a separate Nd:YAG laser. The D2 molecules were contained inside a 50-cm-long cell at a pressure of 60 t, liquid-nitrogen-cooled to reduce the thermal population of upper energy levels and to decrease the Doppler linewidth. The output after the deuterium cell appeared as white light. The generated sidebands were observed after dispersing the beam with a prism.
After the cell exit window, the relative phases of individual sidebands are unknown. To synthesize a prescribed temporal shape, we must adjust the phases of each spectral component, compensating for all dispersive elements in the system.3,4
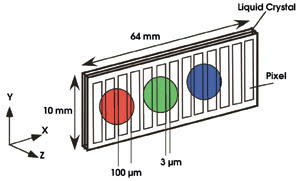
Figure 3. Phase adjustment is performed with a liquid crystal spatial light modulator.
Dispersion control
Because of technical limitations, we work with a seven-sideband subset of the vibrational spectrum, from 410 to 1560 nm. The energy of the components ranges from 2 mJ at 1560 nm to 0.5 mJ at 410 nm. Phase adjustment is performed with a liquid crystal spatial light modulator featuring 640 pixels, each measuring 97 μm × 7 mm and spaced 3 μm apart (Figure 3). Each pixel consists of long birefringent molecules inside two clear electrodes. The electrodes allow independent electric fields to be applied in the Z direction to each pixel, causing the molecules to rotate and thereby changing the refractive index. Having first calibrated the spatial light modulator, we can adjust the phase of each sideband by applying a specified voltage to each pixel.V
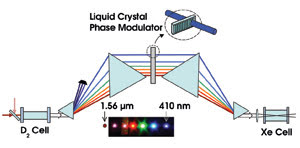
Figure 4. The phase of each of the seven sidebands is adjusted in the phase modulator to produce the desired pulse in the xenon cell.
After the deuterium cell, the seven generated sidebands are dispersed and collimated using two fused silica prisms (Figure 4). All other frequencies are blocked. After collimation, each sideband passes through a range of pixels of the spatial light modulator. The beams are then recombined using another prism pair that mirrors the dispersing prism pair, and they are steered and focused into a xenon chamber. The desired pulse is synthesized in this focal region of overlapping sidebands inside the chamber. The phase adjustment compensates for Gouy phase shift and the optics prior to the focal spot. The ultrashort pulses exist only inside the chamber. Before and after, the relative phases are not known.
Four-wave mixing inside the xenon chamber serves as a pulse shape diagnostic, which enables us to properly adjust the individual phases of the seven Raman sidebands. Focusing the sidebands into the chamber produces a very weak UV signal (in the range of picojoules) at several discrete frequencies resulting from the four-wave-mixing nonlinear process in xenon. The magnitude of this signal depends on the intensity of the synthesized pulse. The shortest possible pulse that can be synthesized also has the highest possible intensity, so we adjust the individual phases to maximize the UV signal. In this manner, the UV signal serves as feedback for adaptive phase adjustment by the spatial light modulator.
Four-wave mixing up-converts the Raman frequencies into the UV. In a typical four-wave process, three wavelengths are combined in a nonlinear medium. The result is the generation of a frequency equal to some combination of the three input frequencies (Figure 5).
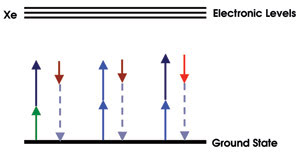
Figure 5. Multiple three-photon paths of Raman frequencies (solid lines) result in the same generated UV frequency (dashed line). The overall UV signal depends on the phases between the different three-photon paths.
Mixing Raman sidebands
In our experiment, we focus tightly into the xenon chamber with an f = 15-cm lens. In this limit, in which the medium is much larger than the confocal parameter, the phase-matching conditions produce radiation whose frequency equals the sum of the frequencies of any two Raman sidebands minus a third. Mixing the seven Raman sidebands, which are equally spaced by 90 THz, generates six UV signals at wavelengths from 365 to 236 nm, with efficiencies of 10–8 or less. The energy at each depends on the relative phases of the Raman sidebands.5
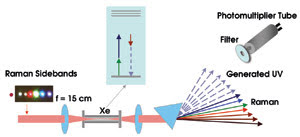
Figure 6. In the four-wave-mixing detector, the UV signal serves as feedback for adaptive phase adjustment by the spatial light modulator.
A solar-blind photomultiplier tube measures the weak UV signal (Figure 6). Because of the very low conversion efficiency to the UV, great care is necessary to attenuate the background radiation. The photomultiplier is placed approximately 2 m from the xenon chamber. Using a fused silica prism, we spatially separate each of the UV components from its neighbors by approximately 10 cm. The scattering of the Raman sidebands from the various optical components in the setup still results in a very poor signal-to-noise ratio. Finally, we use an interference filter with a 1000:1 rejection ratio. The combination of photomultiplier responsivity, beam separation and filtering results in a signal-to-noise ratio of approximately 1000:1.
Once the ultrashort train of pulses has been synthesized, we want to observe and characterize it. Pulses that are shorter than a few tens of picoseconds cannot be measured directly. Instead, we use indirect correlation methods in which part of the pulse is delayed and then combined with the rest of the pulse. By measuring the resulting signal as a function of the delay, we can infer the pulse duration. This type of pulse measurement requires a nonlinear detector; we use four-wave mixing in xenon, a third-order process. Hence, the four-wave mixing serves both as a diagnostic for pulse synthesis and as a means to characterize the pulse shape.
Waveform characterization
We characterize the synthesized waveform by electronically delaying the pulse formed by three of the Raman sidebands with respect to the pulse formed by the remaining four. The synthesized single-cycle waveform can be viewed as the sum of the waveforms formed from these two sets of the interleaving Raman sidebands. Both trains of pulses have nearly the same pulse width and half the pulse spacing as the total waveform. The delay of one pulse train with respect to the other is achieved by adding to each of its three sidebands a phase proportional to the sideband’s frequency.
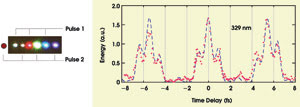
Figure 7. The cross-correlation trace is obtained by electronically delaying pulse 1 with respect to pulse 2. Pulse 1 consists of odd Raman sidebands; pulse 2 consists of even Raman sidebands, as shown.
At each delay interval between the two pulses, we measure the resulting UV signal at one of the UV frequencies. In Figure 7, the red dots represent the UV energy at 329 nm as a function of the delay. The dashed line is the corresponding theoretical plot of the interaction. This plot is the cross-correlation of the two pulses. It has a period of 5.5 fs (one-half the actual pulse spacing) and a cross-correlation width of several femtoseconds. From the agreement between theory and experiment, we conclude that in the synthesized pulse, all the relative phases are the same. The actual synthesized electric field (Figure 8a) is obtained by summing the seven sinusoidal terms at the frequency fn with the corresponding measured field amplitude, An:
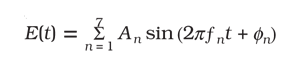
Because the phase of each term is the same, fn = 0.
Synthesized pulses
And because we know the frequencies and relative amplitudes of each of the seven sidebands, we can plot the electric field. The resulting waveform, which is shown in Figure 8a, has a period of 11 fs because of the discreteness of the spectral sidebands. Pulse separation is inversely proportional to the separation of the adjacent frequencies (i.e., 1/90 THz = 11 fs). Note that the electric field changes in phase from one pulse to the next.
The incommensurate frequency comb causes this phenomenon, which is called carrier-envelope slip.
In the spectrum, the frequency difference between adjacent sidebands is not an integer multiple of any one sideband. When the peak electric field coincides with the intensity envelope, the pulse is called a “cosine pulse.” When it is offset by Π/2, the pulse is a “sine pulse.” The pulse width of the cosine pulses is 0.5 fs. Each synthesized pulse has a peak power of more than 1 MW, and there are approximately 106 pulses under the 10-ns envelopes of the Q-switched pump lasers.
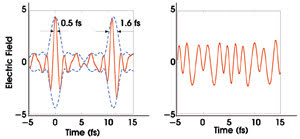
Figure 8. The researchers synthesize single-cycle (a) and frequency-modulated (b) waveforms.
Besides the single-cycle pulse, we also synthesize a frequency-modulated waveform (Figure 8b). After the UV signal is maximized, we conclude that all of the relative phases of the Raman sidebands are the same. We then calculate and add phases to some of the seven sidebands to minimize the generated UV signal. The resulting electric field corresponds to a frequency-modulated like pulse. In all cases, phase stability is extremely good. In our experiments, we have noticed no detectable phase drift among the sidebands during several hours of operation.
Future goals
Having achieved phase control over such a wide-bandwidth source, we are working on its applications to a real system and on further source improvements. To demonstrate shaping of an arbitrary pulse, we need to extend phase control over a larger bandwidth and to increase the number of spectral components that we simultaneously control.
We also are researching systems for which the use of multioctave optical pulses provides a clear advantage over sources with a narrower bandwidth. Another one of our goals is to attain stop-motion photography of molecular movement.6
We believe that our multioctave laser source is a unique tool that, with time, will find many novel applications.
Acknowledgments
The authors thank Alexei V. Sokolov for field-opening contributions in the area of this work. The US Air Force Office of Scientific Research, the US Army Research Office and the US Office of Naval Research supported this effort.
References
1. A.V. Sokolov et al (July 17, 2000). Raman Generation by Phased and Antiphased Molecular States. PHYS. REV. LETT., pp. 562-565.
2. D.D. Yavuz et al (May 2002). Rotational Raman generation with near-unity conversion efficiency. OPT. LETT., pp. 769-771.
3. D.D. Yavuz et al (Dec. 5, 2003). Quasiperiodic Raman Technique for Ultrashort Pulse Generation. PHYS. REV. LETT., 233602.
4. A.V. Sokolov et al (July 16, 2001). Femtosecond Light Source for Phase-Controlled Multiphoton Ionization. PHYS. REV. LETT., 033402.
5. M.Y. Shverdin et al (Jan. 28, 2005). Generation of a Single-Cycle Optical Pulse. PHYS. REV. LETT., 033904.
6. A.V. Sokolov (September 2003). Single-cycle optical pulses synchronized with molecular oscillations. APPL. PHYS. B, pp. 343-347.
Meet the authors
Miroslav Y. Shverdin (e-mail: [email protected]) and David R. Walker (e-mail: [email protected]) are postdoctoral scholars, Sunil N. Goda (e-mail: [email protected]) is a graduate student, G.Y. Yin (e-mail: [email protected]) is a research scientist, and Stephen E. Harris (e-mail: [email protected]) is a professor at Stanford University in California. Deniz D. Yavuz (e-mail: [email protected]) is a postdoctoral scholar at the University of Wisconsin in Madison.
Why Generate Single-Cycle Pulses?
Recently, we synthesized ultrawide-bandwidth optical pulses that have the shortest duration ever achieved using optical frequencies — 1.6 fs — and a repetition rate of 11 fs. These pulses are single-cycle, consisting of a single electrical field oscillation, and have a peak power of more than 1 MW. In addition, we were able to vary the shape of the pulse to generate different prescribed waveforms.
Scientists strive to control chemical and biological interactions by applying laser pulses of different shapes.1-3 A system can be forced into certain states based on the shape of the applied electric field. In the optical regime, however, the shortest pulses produced to date (~4 fs) cover less than one octave of bandwidth, which limits the possible types of waveforms that can be produced. (An octave is an interval of frequencies for which the ratio of the highest to the lowest is 2:1.)
The synthesis of arbitrarily shaped multioctave pulses opens a new frontier of nonlinear optics and coherent control. To obtain full control over a molecular reaction, we need to match the bandwidth of the pulse with the full molecular spectrum. The spectra of most molecular materials span a wide range of frequencies, and now we can simultaneously access that range with our source.
We envision novel applications of multioctave pulses for the coherent control of chemical reactions, as a probe for ever-shorter physical processes, and for the highly efficient generation of far-infrared and vacuum-ultraviolet radiation.
References
1. T. Brixner et al (2001). Advances in Atomic, Molecular, and Optical Physics. Vol. 46. H. Walther and B. Bederson, eds. Academic Press, pp. 1–54.
2. R. Bartels et al (July 13, 2002). Shaped-pulse optimization of coherent emission of high-harmonic soft X-rays. NATURE, pp. 164-166.
3. B.J. Pearson et al (June 2001). Coherent control using adaptive learning algorithms. PHYS. REV. A., 063412.