Quantum-well-pumped semiconductor thin-disk lasers combine the thermal advantages of rare-earth thin-disk lasers and the frequency flexibility of semiconductor lasers.
Svent-Simon Beyertt, Dr. Uwe Brauch and Dr. Adolf Giesen, Universität Stuttgart, Eckart Gerster, Universität Ulm, and Dr. Martin Zorn, Ferdinand Braun Institut für Höchstfrequenztechnik
When the thin-disk laser appeared on the scene more than a decade ago, it was the first solid-state laser capable of efficiently producing a high-optical-quality output in the multikilowatt range.1 Its principle is to use a very thin section of material as the active medium and to cool it through a highly reflective back mirror (Figure 1).
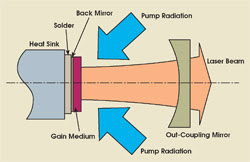
Figure 1. A thin-disk laser is optically pumped at the surface of the gain medium. The MB35 thermal gradient is perpendicular to the surface, enabling the scaling of output power with the pump area.
In this geometry, the thermal gradient is in the same direction as the resonator’s axis, perpendicular to the surface, substantially reducing thermally induced lensing and birefringence and enabling the laser power to increase linearly with the surface area pumped (at constant power density). Of course, this works only if the heat generated can be removed with a purely one-dimensional heat flow without raising the crystal temperature excessively.
Yb:YAG turns out to be an excellent material for the thin-disk laser. It has a small quantum defect — that is, the energy of a pump photon is only slightly greater than that of a laser photon. When pumped at 940 nm, a 1030-nm Yb:YAG laser loses only 11 percent of the pump power to heat, and when pumped at 969 nm, only 6 percent. The material has produced the highest output powers so far in the thin-disk configuration: Models with outputs of up to 4 kW are commercially available.
This type of laser offers other advantages as well. Using various rare-earth ions and host crystals and/or efficient intracavity approaches to second-harmonic generation, discrete laser lines in the infrared and visible spectral regions can be generated — albeit not yet at the kilowatt level.
A variety of materials, however, also show promise for thin-disk lasers. In particular, semiconductors offer an interesting alternative to rare-earth-doped dielectric crystals. The epitaxial growth process is ideally suited to the thin-disk geometry. Furthermore, the wavelength of a semiconductor laser depends on the bandgap between the valence and conduction bands, which in turn depends on the composition of the semiconductor. This flexibility, together with the possibility of efficient harmonic generation, underlies the potential development of semiconductor lasers with outputs over a broad spectral range.
Promises and problems
Closely related devices, although on a much smaller scale, are the vertical-cavity surface-emitting lasers (VCSELs).2 These consist of a highly reflective Bragg mirror underneath one or two quantum wells that are surrounded by barrier layers, with a Bragg mirror atop the device serving as the output coupler. Pumping is electrical, via a PN junction. The short resonator, on the order of a single wavelength, limits the beam diameter for fundamental-mode operation to a few microns and the output power to a few milliwatts.
Substantially boosting the fundamental-mode power requires a longer external resonator to increase the intracavity mode diameter and optical pumping to avoid both excessive resistive-heating and electrode-geometry problems. The thin-disk design satisfies both requirements.
Semiconductor thin-disk lasers are sometimes called vertical-external-cavity surface-emitting lasers (VECSELs) or optically pumped semiconductor lasers. The thinner the disk, the more pronounced the advantages — low threshold, efficient cooling — of this type of laser.
Accompanying a reduction in disk thickness, however, is reduced absorption efficiency, because there is less material through which the pump radiation passes. Special optics that reflect the pump radiation through the disk for multiple passes can alleviate this problem and increase the total absorption efficiency to 90 percent.
Aram Mooradian’s team followed a different approach to the low-absorption problem, known in the solid-state laser community as codoping, or sensitizing, to achieve output powers in the 1-W range.3 In this technique, the layers surrounding the amplifying quantum-well layers — chosen for their bandgap and thickness — absorb the pump radiation effectively in one pass while being transparent to the laser radiation (Figure 2).
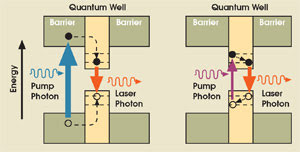
Figure 2. In barrier pumping (left), a pump photon is absorbed in the barriers surrounding the quantum well, where it creates an electron-hole pair. The pair migrates to one of the wells, where it recombines to create a laser photon. In quantum-well pumping (right), the pump photon is absorbed in the quantum well, thereby creating an electron-hole pair. After relaxation to the ground state, it recombines into a laser photon. The difference in energy between pump and laser photon — the quantum defect — is deposited as heat.
In the research reported so far on semiconductor thin-disk lasers (see reference 4 for an overview), output powers have been ~1 W, and the pump spots have been sufficiently small to stay in the efficient three-dimensional cooling regime. With another diamond heat spreader, which further extends this cooling regime, a maximum output of 30 W could be realized from a 0.9-mm pump spot.5
Direct pumping
As ingenious as this method is to independently optimize transparency threshold and absorption efficiency, it also has a disadvantage: The energy of the pump photon as a rule must be 20 percent larger than that of the laser photon. This quantum defect is transformed into heat, which must be removed through the Bragg mirror to a heat sink. Considering that these lasers are pumped with a typical 10 kW/cm2, a thermal load of 20 percent of the pump power can be detrimental.
True power scaling requires the use of less-efficient, purely one-dimensional heat flow perpendicular to the disk surface for cooling.6 To keep the temperature of the active layers at a reasonable level, the heat generated in the semiconductor disk must be minimized. Pumping as close as possible to the laser wavelength can reduce the quantum defect, which is a major contributor to the heat generation. Our group has done this by pumping directly into the quantum wells, using the same transition for absorption and for emission.
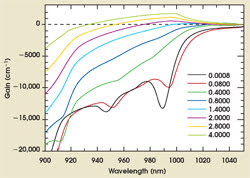
Figure 3. The curves show the calculated gain and absorption spectra (positive and negative numbers, respectively) of an 8-nm-thick InGaAs quantum well for various carrier densities (in units of 1012/cm2). Transparency at the laser wavelength is at ~1.4 × 1012/cm2. Depending on the number of quantum wells, a gain of several hundred per centimeter is necessary to yield a round-trip gain of 1 to 2 percent, which requires a carrier density of ~1.6 × 1012/cm2. At this density, absorption is reduced from 13,000 cm–1 to 3000 cm–1 at the pump wavelength of 940 nm. Pumping at wavelengths shorter than 900 nm would strongly reduce the bleaching effect, at the cost of a somewhat increased heat load.
The challenge is that a single quantum well absorbs perhaps only 1 percent per pass, and even less when it is pumped to a carrier density needed to reach transparency on the laser transition (Figure 3). Increasing the number of quantum wells directly improves the absorption simply by lengthening the total absorption. At the same time, the bleaching is reduced because each well has less gain to produce, thus decreasing the carrier density per well required to reach threshold. On the other hand, the absorbed pump power necessary to reach transparency grows proportionally to the number of quantum wells, which sets an upper limit on the number of useful wells of perhaps 10 to 20.
Increasing the pump absorption further — the prerequisite for good overall laser efficiency — requires the pump radiation to pass the quantum wells several times. There are two ways to do this, one or both of which can be used in a given case:
• Use external pump optics, which reflect the pump radiation for multiple passes through the gain medium.
• Take advantage of the Fabry-Perot resonator formed by the uncoated top surface of the semiconductor disk and highly reflective Bragg mirror at the bottom, a technique that is known as resonant absorption.
Traditionally, standing-wave effects in VCSELs and VECSELs have been considered only for the laser field. There is no need to do so for the pump radiation when highly absorbing barrier layers are present. To take advantage of the standing waves, the quantum wells must be placed at the antinodes of the standing-wave pattern with a separation of λlaser /2, because the standing wave has two antinodes per λlaser (Figure 4). In this way, the intensity at the quantum wells is twice the average intensity.
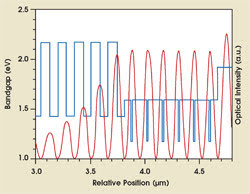
Figure 4. The cross section of a semiconductor thin disk shows six quantum wells (with bandgap energy of 1.2 eV) on the right and the Bragg mirror on the left. The quantum wells are positioned at the antinodes of the standing laser field intensity (red line).
The intensity is further enhanced by the resonator — whether the internal resonator of a VCSEL or the long external resonator of a VECSEL. Often, the VECSEL semiconductor surface is uncoated, resulting in an additional internal resonator formed by the Fresnel reflection from the top of the disk and the Bragg reflector on the bottom. The length of the internal cavity must be carefully adjusted to the laser wavelength and the quantum-well spacing. The longitudinal mode density of the external resonator is so high that there is always a mode that fits the internal resonator/quantum-well spacing.
The situation becomes more complex in resonant absorption, where the resonances of the internal resonator as well as the quantum-well spacing are optimized for both the pump and laser fields. In this way, the pump intensity at the quantum wells can be enhanced by twice the Q factor of the internal resonator, which is determined by the reflectance of its mirrors; the factor of two comes from the placement of antinodes.
To accomplish this, the device must be designed so that the antinodes of both the laser and the pump radiation lie at the locations of the quantum wells. Because the pump wavelength is necessarily shorter than the laser wavelength, the antinodes of the two fields can be brought into alignment by increas-ing the angle of incidence of the pump radiation (see the end note). For a given pump radiation wavelength λpump, the internal pump angle α' must satisfy the condition λpump(α') = λlaser (0°)cos(α').
When calculating α', one must take into account that the corresponding external angle is much larger because of a typical index of refraction of 3.5. A difference of –30 nm in pump and laser wavelength therefore requires an external angle of 70°.
A positive side effect of the large angles involved is increased Fresnel reflectance for the s-polarization — and with it an increased Q for the internal resonator. This leads to a higher field improvement inside the cavity, further enhancing the on-resonance absorption.
Unfortunately, the higher the Q factor of the internal cavity, the narrower the resonance lines in terms of wavelength and angle. The high divergence and linewidth of a typical fiber-coupled diode array pump source negates much of the advantage of resonant pumping. To compensate, external pump optics — a concave mirror in the simplest case — can reflect the transmitted pump radiation several times through the medium.
Head-to-head matchup
To compare quantum-well and barrier pumping, we examined the performance of a thin-disk semiconductor laser pumped at 940 nm and at 800 nm under otherwise identical conditions. In the first experiment, we pumped a relatively small spot at low powers with a Ti:sapphire laser; in the second, we pumped a larger spot, using fiber-coupled diode lasers.
The semiconductor disk used in the Ti:sapphire experiment had six InGaAs quantum wells emitting near 980 nm, and the laser’s geometry was designed for resonant pumping. For barrier pumping, the Bragg mirror at the bottom of the laser had a second reflectance peak at 800 nm to reflect the pump radiation for another pass through the gain medium. For quantum-well pumping, an external lens/mirror combination reflected the unabsorbed pump radiation for a second double pass through the gain medium.
The three major experimental findings were:7
• Although a plot of laser power versus incident power showed slightly higher efficiency for barrier pumping at low powers, a plot of laser power versus absorbed power showed higher efficiency for quantum-well pumping (Figure 5).
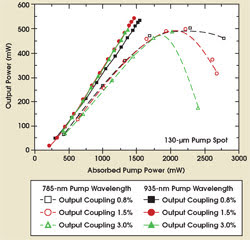
Figure 5. The efficiency with respect to absorbed power was slightly higher for quantum-well pumping (solid lines) than for barrier pumping (broken lines).
• The absorption efficiency for quantum-well pumping was as high as 70 percent, with only a single reflection through the gain medium (i.e., two double passes).
• The increase in temperature in the gain medium with absorbed pump power was 17 K/W for barrier pumping and 6 K/W for quantum-well pumping, so the thermal load for the latter was a factor of three smaller. (For perspective, if the only contribution to the thermal load were the quantum defect, one would expect a factor of 4.3.)
The sample in the laser diode experiment had 13 quantum wells. For barrier pumping, we directed the 800-nm radiation from a fiber-coupled diode array directly onto the sample at an angle of incidence of 30°. The Bragg reflector at the bottom was not designed to reflect this wavelength. For quantum-well pumping, we used a pump optics arrangement that was originally designed for use with Yb:YAG and that offered 24 single passes of 938-nm pump radiation. The resulting pump spots had diameters of about 300 μm.
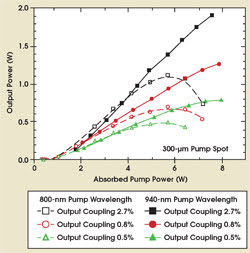
Figure 6. Thermally induced rollover dramatically reduces the output power in barrier-pumped thin-disk lasers (broken lines). The output in quantum-well-pumped devices (solid lines) is limited only by the available pump power.
The laser power as function of absorbed pump power is shown in Figure 6. Again, the power curves for barrier and quantum-well pumping are similar at low power. These slopes show more pronounced differences for different values of output coupling, and they generally are lower than those measured in the previous experiment. These differences probably are a result of higher resonator losses. For higher powers, thermally induced rollover starts much earlier when the laser is barrier pumped, limiting the output power to 1.2 W.
By pumping directly into the quantum wells, we achieved 1.9 W of output, limited only by the available pump power — another indication of the reduced heat generation with quantum-well pumping.
End note
One may be inclined to presume that the path length of the incident beam inside the cavity is relevant to the cavity resonance. Because the path length is longer for oblique than for normal incidence, one would imagine that the pump wavelength must be longer than the laser wavelength. But this is not the case.
Consider the standing-wave pattern formed by the superposition of incoming and reflected waves of wavelength λ. Its periodicity along the cavity axis is given by λsw(α', λ) = λ/cos(α'). Therefore, to keep both pump and laser radiation in resonance with the cavity requires λsw(0°, λlaser) = λsw(α', λpump). Hence, λpump = λlasercos(α').
Meet the authors
Svent-Simon Beyertt (e-mail: [email protected]) is a PhD student, Uwe Brauch (e-mail: [email protected]) is a research fellow, and Adolf Giesen (e-mail: [email protected]) is head of the laser and optics department at the Institut für Strahlwerkzeuge at Universität Stuttgart in Germany. Eckart Gerster (e-mail: [email protected]) is a PhD student in the optoelectronics department at Universität Ulm in Germany. Martin Zorn (e-mail: [email protected]) is a research scientist at Ferdinand Braun Institut für Höchstfrequenztechnik in Berlin.
Acknowledgment
This work was funded by Landesstiftung Baden-Württemberg GmbH of Stuttgart, Germany.
References
1. A. Giesen et al (May 1994). Scalable concept for diode-pumped high-power solid-state lasers. APPL. PHYS. B, pp. 365-372.
2. K. Iga (November/December 2000). Surface-emitting laser — its birth and generation of new optoelectronics field. IEEE JOURNAL OF SELECTED TOPICS IN QUANT. ELECT., pp. 1201-1215.
3. M. Kuznetsov et al (May/June 1999). Design and characteristics of high-power (>0.5-W CW) diode-pumped vertical-external-cavity surface-emitting semiconductor lasers with circular TEM00 beams. IEEE JOURNAL OF SELECTED TOPICS IN QUANT. ELECT., pp. 561-573.
4. A.C. Tropper et al (May 2004). Vertical-external-cavity semiconductor lasers. J. PHYS D: APPL. PHYS., pp. R75-R85.
5. J.L.A. Chilla et al (July 2004). High-power optically pumped semiconductor lasers. Proc. SPIE — Solid State Lasers XIII: Technology and Devices, pp. 143-150.
6. A.J. Kemp et al (February 2005). Thermal management in vertical-external-cavity surface-emitting lasers: finite-element analysis of a heatspreader approach. IEEE JOURNAL OF QUANTUM ELECT., pp. 148-155.
7. S.-S. Beyertt et al (2005). Semiconductor Thin-Disk Laser Comparison of Spacer and Quantum-Well Pumping. Advanced Solid-State Photonics Topical Meeting, Poster Mb35.