By filtering out a multitude of high-order modes, these novel semiconductor lasers emit a large single-mode beam.
Robin K. Huang, Bien Chann, Leo J. Missaggia and Joseph P. Donnelly, MIT
Since the invention of diode lasers in 1962, researchers have sought to increase the power available from them in a single spatial mode. Because of their high brightness, single-mode diode lasers have many advantages for a variety of applications. Single-mode, high-power diode lasers are used to pump erbium-doped fiber amplifiers that are essential to fiber optical communications. Others pump fiber lasers in a number of commercial and industrial applications, but the amount of pump light that can be coupled into the fiber is generally limited by the diode’s low beam quality.
In another example, diode lasers are of interest for being used directly in materials processing, and their efficacy depends on their brightness because the beam intensity on a distant workpiece can be dramatically increased by increasing the source’s brightness. Brightness is also important for diode lasers in free-space optical communications because the fractional amount of the transmitter’s light that reaches the receiver is proportional to brightness.
Numerous methods have been employed to boost the single-mode output power from a diode laser. Although the power that is available from conventional single-mode ridge lasers keeps rising, these increases have been incremental, and optical loss and heat removal impose definite limitations. Moreover, ridge-waveguide lasers1 usually have highly elliptical beams that diverge much more rapidly in one axis than in the other. External optics are necessary to couple these beams into a single-mode fiber.
Tapered lasers2 have been developed to increase the mode in the lateral direction while keeping the device in a single mode. These lasers use an adiabatic taper along their length to enlarge the optical mode, but these structures suffer from beam instability problems at high powers, and heroic optics are needed to couple the astigmatic output beam to a fiber.
The slab-coupled optical waveguide laser (SCOWL) is a recent invention of MIT’s Lincoln Laboratory in Lexington, Mass., that eliminates the problems of wide divergence in the fast axis and the resulting elliptic mode profile. In conventional diode lasers, these problems originate from the necessary trade-offs between carrier and optical confinement. In the SCOWL concept, a gain region is carefully incorporated into a large slab-coupled optical waveguide.3 In this way, it is possible to achieve a single-spatial-mode laser with a large intracavity beam that is diffraction-limited in both axes.
Many advantages result from this concept, including reduced thermal loading, low power density at the end facets and the possibility for direct butt-coupling with high efficiency into a single-mode fiber.
In a SCOWL, the beam is expanded in the transverse (Y) direction, perpendicular to the plane of the device, such that the fast and slow directions of the laser mode can be made nearly equal in dimension. A thin gain region carefully placed within a large, low-loss, passive waveguide results in a low modal loss, which allows the construction of longer devices, spreading out the heat and reducing series resistance. The net result is high power in large, nearly circular, diffraction-limited mode. This mode profile is ideally suited, for example, for efficient coupling into a single-mode fiber.
The brightness (B) of a laser is expressed by:
B = P/( λ2 Mx2 My2 ),
where P is the power emitted from the laser, λ is the laser wavelength and Mx2 and My2 are the beam quality parameters in the vertical and horizontal directions, respectively. Clearly, brightness is highest for the lowest mode order. Brightness is the metric that measures, for example, the amount of power that can be delivered on a far-field target. The differences in brightness between multimode and single-mode lasers can be large; e.g., a typical multimode pump laser with P = 1 W, λ = 1 μm, Mx2 = 1, and My2 = 20 has B = 5 MW/cm2-sr. On the other hand, a single-mode laser — e.g., a SCOWL — with P = 1 W, λ = 1 μm, and Mx2 = My2 = 1 has B = 100 MW/cm2-sr. The multimode laser would have to be 20 times more powerful than the single-mode one to produce equivalent brightness.
Slab coupling
The SCOWL uses the concept of slab coupling in which high-order modes of a large waveguide are filtered out by coupling to slab modes, thereby transforming this multimode waveguide into a single-mode one. More than 30 years ago, Enrique A.J. Marcatili used the coupled-mode theory to show that an arbitrarily large slab-coupled passive waveguide should be possible.3 In Figure 1, the large, round fiber can propagate many modes. When the fiber is brought close to the slab, its modes couple to those of the slab. If only the lowest-order fiber mode has a propagation constant higher than the propagation constants of the slab mode (ßz-slab in the figure), the high-order fiber modes will couple to the slab, leaving the composite structure with only one bound mode; that is, the composite structure will be single-moded.
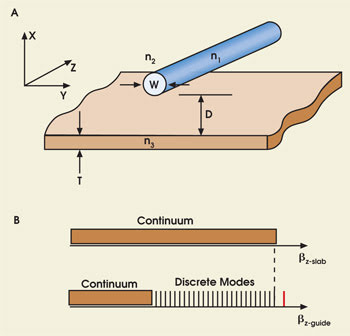
Figure 1. A large multimode waveguide (diameter W) is brought close to (distance D) a slab of thickness T (A). In the propagation constant picture (B), one considers the overlap of the continuum slab modes with the higher-order waveguide modes. If the overlap is designed carefully with respect to dimensions W, D and T, the composite slab-waveguide system is single mode (fundamental mode indicated in red). ß = (2π/λ) × modal index.
Marcatili’s analysis is straightforward, but reality is more complicated. Even though there is only one true bound mode, other slowly decaying, or “leaky,” modes can exist. These can be problematic in lasers, but they are often an issue even in purely passive guides because they can be inadvertently excited at the input, and it takes a long distance for them to radiate away. Indeed, we deal with leaky modes all the time. Propagation in curved waveguides really occurs via leaky modes, as does propagation in AlGaAs waveguides on GaAs substrates, because the substrate has an index greater than or equal to that of the guide.
For good single-mode operation in a slab-coupled guide, all potential leaky modes should couple efficiently into the slab so that they will radiate away quickly. If they don’t couple efficiently and their coupling loss is less than their gain, they will reach threshold and oscillate. For the leaky modes to be sufficiently lossy, they must be well-coupled to one or more slab modes that have higher propagation constants.
The coupling efficiency depends on the overlap between the two modes in the Y direction, which in turn depends on the geometry.
For example, Figure 2 shows good overlap between the fourth rib mode and the third slab mode. Clearly, this picture depends on the geometry; that is, the thickness of the rib and of the slab. As shown here, it’s fairly easy to get rid of a particular higher-order rib mode. The trick is to find a waveguide geometry that eliminates them all. This task becomes more difficult as the guide gets larger.
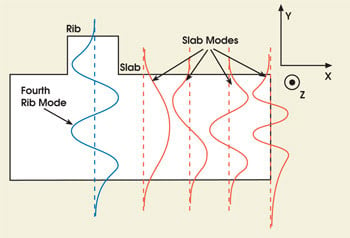
Figure 2. The fourth rib mode (blue) has substantial spatial overlap with the third of the four slab modes shown. In this case, the higher-order rib mode may be filtered by the slab.
Complicating the picture further, gain-guiding (guiding via the imaginary part of the index) comes into play when gain is added. Therefore, our slab-coupled waveguide laser must have low gain to avoid gain-guiding of high-order modes. If the gain is low, the loss of the favored single mode also must be very small. To take all these factors into account and design a successful laser, we use a two-dimensional, complex index mode solver. The simple ideas already described define a good starting point, but numerical simulation of the structure is required for a quantitative description. The result is the SCOWL structure (Figure 3).
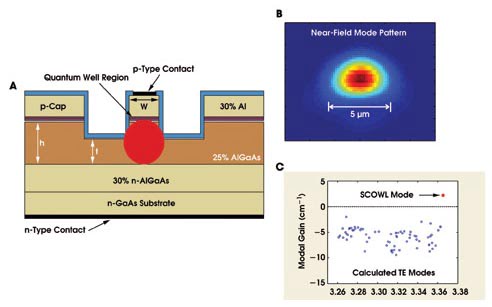
Figure 3. This schematic is a cross-sectional view of a 980-nm slab-coupled optical waveguide laser with three strained InGaAs quantum wells, GaAsP barriers and bounding and nominal dimensions of h = 5.0 μm, w = 5.7 μm and t = 4.5 μm (above). The measured near-field profile of the SCOWL mode is nearly perfectly round (right). The typical dimension of this optical mode is approximately 5 μm in both axes. A calculation of the transverse electric modes of the device shows that only the single SCOWL mode is above threshold (top right).
In this structure, we placed the gain region (the “quantum well region” in the figure) on top of the thick waveguide to prevent the mode from becoming localized about the active region. In the mode solver calculations, real and imaginary (gain and loss) indices based on composition and doping were assigned to all the device layers. The outer regions were retained because, in the actual structures, they were used to facilitate junction-side-down mounting. The loss in the unpumped gain regions in these outer regions also contributes to loss in the higher-order modes while not affecting the lowest-order SCOWL mode. Because of the artificial boundary, the lossy radiation modes are made discrete.
The rib width and etch depth were varied to determine the range over which the structure would have only one mode with modal gain. For any particular structure, if the gain is increased too much, one or more higher-order modes will become gain-guided and move into the modal gain region.
The calculated transverse electric modes (fundamental and higher order modes) of the 980-nm SCOWL structure are shown in Figure 3. This calculation is related to the schematic diagram of Figure 1, in which the (red) fundamental mode is isolated from numerous higher-order modes by slab coupling of passive waveguide modes.
In the case of the laser, the (red) SCOWL mode is isolated from numerous higher-order modes by slab coupling. For the laser, the key parameter is the modal gain, which serves to isolate the fundamental mode from the higher-order ones.
Applications
SCOWLs have been demonstrated at several laser wavelengths, including 915 and 980 nm, and 1.3, 1.5 and 2.0 μm. The 980-nm lasers have demonstrated the highest output power levels so far. Their active region typically consists of three InGaAs strained quantum wells (Figure 3), and both the waveguide and cladding layers are fabricated from AlGaAs. Low-loss materials in the waveguide are essential to maintain the low optical waveguide loss.
These lasers can be fabricated with cavity lengths ranging from 300 μm to 1 cm. The longer lasers can generally emit more than 1.25 W continuous wave,4 with a beam quality of M2 = 1.1.5 The brightness at this level is approximately 107 MW/cm2.sr, equivalent to that of a typical 25-W multimode diode laser. The temperature rise in these long lasers is reduced dramatically because the heat is distributed along their entire length. We obtain large, nearly circular output beams, with 1/e2 waists of the near field of about 5.7 (horizontal) by 4.2 μm (vertical). With the large optical mode, an excellent mode match can be obtained with that of a single-mode fiber, and >800 mW has been butt-coupled (using no coupling lens) directly to a single-mode fiber.4
SCOWL amplifiers also have been demonstrated at a wavelength of 1.5 μm.6 They are fabricated using InGaAsP/InP materials. In these amplifiers, the SCOWL ridge is oriented at an ~5° angle relative to the cleaved facets to minimize reflective feedback and to frustrate laser oscillation. The amplifiers provide 10-dB gain and a saturated power that is greater than 500 mW, which is one of the highest reported for a semiconductor optical amplifier at this wavelength.
In addition, passive mode-locking was demonstrated recently with SCOWLs.7 The first section of these two-section lasers is for gain, while the second is a saturable absorber. For 1.5-μm SCOWLs, ~60 pJ of pulse energy has been demonstrated with an average power of 250 mW. For 980-nm devices, similar pulse energies have been generated with average powers of more than 400 mW.8 These are the highest average power levels and pulse energies reported for electrically pumped, mode-locked semiconductor lasers.
Brightness scaling
We have used 980-nm SCOWLs in power- and brightness-scaling experiments, constructing laser arrays with pitches of 100 μm and cavity lengths of 3 mm.9 High-quality array packaging is critical to minimize the temperature rise during high-power operation. These arrays consist of 100 elements (1 cm wide × 3 mm long) and can produce 90 W in CW operation (Figure 4).
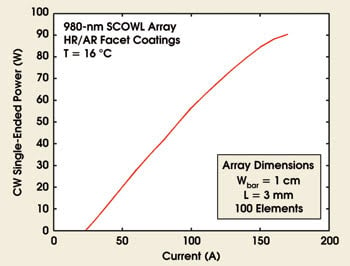
Figure 4. Under continuous-wave operation, a 980-nm SCOWL array consisting of 100 elements (3-mm cavity length and 10-mm bar width) achieves 90 W (HR/AR = high-reflecting/antireflecting).
We also have used these arrays to demonstrate high-power wavelength beam combining.10 In this technique, the individual beams from an array, each at a different wavelength, are combined spatially (Figure 5). In exchange for the higher spatial brightness, however, the spectral brightness is diminished because the bandwidth of the combined beam is equal to the total bandwidth of all the individual lasers. The technique involves an external grating, which, in combination with an output coupling mirror, provides feedback to each laser in the array, wavelength-locking each laser at a distinct wavelength.

Figure 5. A 980-nm SCOWL array is placed within a wavelength-beam-combined external-cavity module.
Using this technique with SCOWL arrays, we have demonstrated a peak power of 50 W under quasi-CW operation with an M2 of 1.2, which is nearly ideal.11 The spectral bandwidth of the combined beam was approximately 15 nm. The brightness of this array, 3.6 GW/(cm2-sr), is one of the greatest reported from a single-diode-laser bar. Under purely CW operation, we have obtained 30 W with M2 = 2. Such systems are inherently scalable, and we anticipate that kilowatt-class, all-diode, nearly diffraction-limited laser sources will become possible before long.
Meet the authors
Robin K. Huang and Bien Chann are technical staff members at Lincoln Laboratory, MIT, in Lexington, Mass.; e-mail: [email protected] and [email protected].
Leo J. Missaggia is an associate staff member at Lincoln Laboratory; e-mail: [email protected].
Joseph P. Donnelly is a senior staff member at Lincoln Laboratory; e-mail: [email protected].
References
1. P. Unger (2000). “Introduction to Power Diode Lasers” in High-Power Diode Lasers: Fundamentals, Technology, Applications, Vol. 78, R. Diehl, ed. Springer-Verlag, pp. 1-53.
2. J.N. Walpole (June 1996). Semiconductor amplifiers and lasers with tapered gain regions. OPT QUANTUM ELECTRON, pp. 623-645.
3. E.A.J. Marcatili (April 1974). Slab-coupled waveguides. BELL SYSTEM TECH JOUR, pp. 645-674.
4. J.P. Donnelly et al (February 2003). AlGaAs/InGaAs slab-coupled optical waveguide lasers. IEEE J QUANTUM ELECTRON, pp. 289-298.
5. R.K. Huang et al (July 2003). High power, nearly diffraction limited AlGaAs-InGaAs semiconductor slab-coupled optical waveguide laser. IEEE PHOTON TECH LETT, pp. 900-902.
6. P.W. Juodawlkis et al (February 2005). High-power 1.5-μm InGaAsP-InP slab-coupled optical waveguide amplifier. IEEE PHOTON TECH LETT, pp. 279-281.
7. J.J. Plant et al (January 2006). 250 mW, 1.5 μm monolithic passively mode-locked slab-coupled optical waveguide laser. OPT LETT, pp. 223-225.
8. J.T. Gopinath et al (May 2006). High power monolithic passively mode-locked slab-coupled optical waveguide lasers. Conference on Lasers and Electro-Optics.
9. R.K. Huang et al (May 2005). High-brightness slab-coupled optical laser arrays. IEEE PHOTON TECH LETT, pp. 959-961.
10. B. Chann et al (August 2005). Near-diffraction-limited diode laser arrays by wavelength beam combining. OPT LETT, pp. 2104-2106.
11. R.K. Huang et al (May 2006). High power, high brightness wavelength-beam-combined diode arrays. Conference on Lasers and Electro-Optics.