This new approach may provide a path to efficient, single-mode, multikilowatt fiber lasers.
Dr. Michael Bass and Dr. Martin C. Richardson, CREOL
In the past decade and a half, fiber lasers with very high multimode output powers have been developed by doping the core of such fibers with ions that can lase. These fiber lasers are pumped by light from diode-laser arrays that is coupled into both the core and the cladding, exciting ions over the entire length of the fiber.
An inherent problem with these powerful lasers is that they cannot readily be made to oscillate in a single transverse mode, so the beam quality is not suitable for some applications. Single-mode oscillation requires a small core, typically 8 to 10 μm in diameter. Larger cores allow high-order modes to oscillate. But the small core leads to high intensities, and high intensities propagating over long distances lead to deleterious nonlinear effects such as stimulated Raman and Brillouin scattering. Many researchers have proposed clever ways of avoiding the nonlinearities, but not one of these to date has provided the robustness and reliability suitable for all applications.
Index-antiguided fiber
An alternative type of fiber laser has been demonstrated in our lab at CREOL at the University of Central Florida’s College of Optics and Photonics in Orlando. This laser oscillates only on the lowest-order transverse mode, and because the core can be large, the optical intensity in the core will be limited, so the laser can be scaled to very high powers.
When you think of an optical fiber, you automatically assume that the core has an index of refraction that is greater than that of the cladding. Light traveling in the core is totally internally reflected from the core-cladding interface and can travel for great distances with minimal loss. Such fibers are the basic transmission mechanism of our modern telecommunications systems. But unlike conventional optical fibers, the fiber we demonstrated does not rely on total internal reflection to confine light to the core. Indeed, the refractive index of the cladding is greater than that of the core, so that the fiber is index-antiguided. Light generated in the core of the fiber can leak out into the cladding, though it experiences some guiding by grazing incidence Fresnel reflection at the core-cladding interface. However, there is loss at each reflection, so the fiber cannot sustain propagating modes the same way a traditional index-guided fiber does.
Now consider what happens when the core of an index-antiguided fi-ber is doped with lasing ions and optically pumped. If pumped hard enough, a point is reached where the gain between core-cladding reflections is equal to the loss at each reflection. This point is the threshold for what is called “gain-guiding,” where propagation through a length of fiber takes place with no net loss. This threshold is different from the threshold for laser oscillation: Laser threshold occurs when the total gain during a round-trip of the laser resonator becomes equal to the round-trip loss.
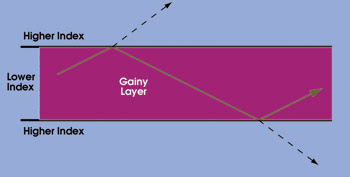
Figure 1. This sketch shows the principle of gain-guided propagation in an index-antiguided fiber. The angles are exaggerated for clarity. If the gain per bounce in the gainy layer equals the loss per bounce, the light experiences no net loss in propagating in the gain-guided index-antiguided fiber.
In gain-guiding, the gain in the “gainy layer” between core-cladding reflections is greater than the loss at the reflection, so a propagating mode is possible without index-guiding (Figure 1). In 2003, Anthony E. Siegman proposed such gain-guiding in fibers with very small but negative differences between the index of refraction of the core and the cladding of a fiber.1 He also showed that the threshold for gain-guiding is mode-dependent, and that low-order modes reach the gain-guiding threshold first. In subsequent work he found that, for large negative index-of-refraction differences, the threshold required to guide the lowest-order LP01 mode is 39 percent of that required to guide the next-higher LP11 mode, and that ratio is independent of core dimension.2
That is a crucial consideration, and it is the reason why gain-guided lasers oscillate only in the lowest-order transverse mode. Once the threshold for gain-guiding has been achieved, more gain is required to overcome other resonator losses (e.g., output coupling) to reach the threshold for lasing. But when laser threshold is attained, the gain saturates at the threshold value and never goes any higher. Assuming that lasing threshold occurs at a lower gain than the gain-guiding threshold for the modes higher than LP01, the higher modes will never reach threshold. Thus, the laser oscillates only in the lowest-order mode, independent of pump power or core size.
Laboratory experiments
In the laboratory, we performed initial experiments to demonstrate this form of gain-guiding, using a fiber with flashlamp pumping.3 Although flashlamp pumping does not allow evaluation of the potential efficiency of such fiber lasers, we demonstrated several very important properties of this laser, including spectral narrowing, relaxation oscillations and lowest-order mode oscillation at pump inputs well above lasing threshold. We believe that compact, very high power, singlemode fiber lasers may be possible based on the gain-guiding principle. However, as we will explain below, pumping geometry and thermal management will be critical issues.
Our fibers were drawn by John Ballato at Clemson University from preforms made by Kigre Inc. of Hilton Head, both in South Carolina. We started with a neodymium-doped, phosphate-glass fiber with a core diameter of 100 μm and an outer cladding diameter of 250 μm. Kigre measured the refractive index of the core at 590 nm to be 1.5689 and that of the cladding to be 1.5734. Because both glasses experience similar dispersion, the negative difference is maintained into the infrared, resulting in an index-antiguided fiber at the lasing wavelength of 1052 nm.
The core medium was Kigre’s Q100 laser glass with 10 percent neodymium doping, which has an index of refraction that decreases with increasing temperature: dn/dT = –4.0 × 10–6/°C. Most glasses, presumably including the cladding of this fiber, have a refractive index that increases with temperature. This unusual behavior for the core glass is very important for index-antiguided fibers because pumping heats the glass. If the core index decreases with increasing temperature, the fiber will always be index-antiguided, even at elevated temperatures.
For the flashlamp-pumped laser experiment, the ends of the fiber were polished flat and as nearly parallel as possible. When polished, the fiber was ~130 mm long, and we inserted it into an ~120-mm-long glass capillary for physical support. (The gain-guided, index-antiguided fiber must be held straight for it to oscillate.) We placed a totally reflecting mirror in contact with the back end of the fiber and left the 4 percent Fresnel reflection from the front facet to serve as the output coupler.
The pump pulse was ~350 μs long, and the lamp fired once per second. The lamp diameter was ~6 mm, and its output was side-coupled into the fiber with a diffuse reflector. The size mismatch between the 6-mm lamp and the 0.1-mm core was one reason for the low (3 × 10–4) coupling efficiency, and the spectral mismatch was another. Future refinements would address both these considerations.
A standard measurement of the beam quality yielded an M2 value of ~1.5 in both horizontal and vertical directions.4,5 This measurement and other observations listed below convinced us that the 100-μm core was supporting lasing action in only the lowest-order LP01 mode. As long as the totally reflecting mirror was in place:
• There was a clear threshold (~15 J) above which the output, though small in absolute terms, increased dramatically.
• Above laser threshold, we observed relaxation-oscillation spikes — an unambiguous signature of laser action.
• The output spectrum at 1052 nm narrowed from ~10 nm to less than 1 nm when the laser reached the threshold.
• The beam spatial distribution narrowed significantly above threshold and corresponded to a beam with angular divergence expected for an LP01 mode coming from the 100-μm-diameter core of the fiber (i.e., 13.4 mrad). This is shown in Figure 2.
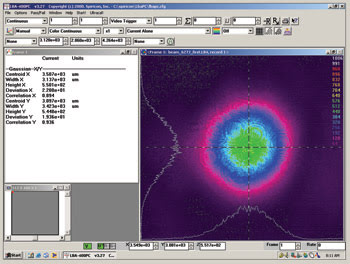
Figure 2. This Spiricon beam-profiler image shows the output beam 152 mm from the output end fiber when pumped at about three times threshold.
• The 1.5 ±0.15 value of M2 in both the horizontal and vertical directions remained unchanged, within the experimental measurement uncertainty, over an input energy range from threshold to about six times threshold. This is exactly what would be expected for lasing in a gain-guided, index-antiguided fiber laser.
It is conceivable that all the observations above could result from an unguided, free-space mode between the back mirror and the front facet of the fiber. To eliminate this possibility, we calculated the Fresnel number of the resonator. The Fresnel number is given by the expression Nf = a2/λL, where a is the resonator-mirror radius (in our case, it is the fiber radius), λ is the laser wavelength, and L is the resonator’s physical length. The diffraction losses for free-space modes in a resonator increase dramatically as the resonator’s Fresnel number, Nf, decreases below one. Because the fiber had a core diameter of 100 μm and was 13 cm long, its Fresnel number was 0.018 when lasing at 1052 nm. Losses for the lowest-order free-space mode in this fiber were very, very large (>10 dB per transit), whereas the round-trip gain of our resonator was only 5 dB. The losses for higher-order modes are even higher. Therefore, there is no possibility of free-space mode oscillation in the current laser setup.
Subsequently, we have demonstrated single-mode oscillation in 200-μm-diameter-core gain-guided, index-antiguided fibers, by paying careful attention to the interplay between the gain-guiding thresholds of the two lowest-order modes and that required for laser threshold.4 These results were obtained at pump powers up to 10 times threshold, showing that the single-mode operation is very robust against breaking into multimode outputs.
We recently applied the concepts developed in the flashlamp-pumped laser experiments to a diode-pumped, end-pumped laser and again obtained robust single-mode operation. End-pumping an index-antiguided fiber is not as simple as it sounds at first. Because pump light can be trapped in the cladding, it may not get into the core, which could lead to significant inefficiency and limited scalability. Side-pumping with diode-pumped sources that are properly tailored to the absorption features of the gain medium can be efficient, and it scales with the length of the fiber. As a result, we are exploring this possibility as an approach to high-average-power, single-mode fiber lasers. As with any laser, issues of thermal management and the removal of waste heat are critical to further development.
With sufficient doping levels, fiber lengths from a few centimeters to several meters may be all that is necessary for laser operation with either end- or side-pumping. The latter becomes feasible with a heavily doped, large-diameter core so that pump light is efficiently absorbed. The properties of gain-guided, in-dex-antiguided fiber lasers may offer a path to efficient, single-mode, multikilowatt fiber lasers.
Acknowledgment
This work was sponsored by DoD JTO MRI contract W911NF-05-1-0517.
Meet the authors
Michael Bass is professor emeritus of optics, physics and electrical and computer engineering at the Center for Research and Education in Optics and Lasers (CREOL) at the University of Central Florida in Orlando; e-mail: [email protected].
Martin C. Richardson is the Northrop-Grumman professor of x-ray photonics and a professor of optics, physics and electrical and computer engineering at CREOL; e-mail: [email protected].
References
1. A.E. Siegman (2003). Propagating modes in gain-guided optical fibers. J OPT SOC AM, Vol. 20, pp. 1617-1628.
2. A.E. Siegman (2007). Gain guided, index antiguided fiber lasers, J OPT SOC AM B, to be published.
3. A.E. Siegman et al (December 2006). Confined propagation and near single mode laser oscillation in a gain guided, index anti-guided optical fiber, APPL PHYS LETT, 251101.
4. Ying Chen et al (January 2007). Experimental demonstration of gain guided lasing in an index anti guiding fiber, Advanced Solid-State Photonics, Vancouver, Canada.
5. ISO 11146-1:2005, Lasers and laser-related equipment — test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams.