Acousto-optic beam shaping brings a new dimension to adaptive optics.
Craig B. Arnold and Euan McLeod, Princeton University
When it comes to shaping the intensity patterns or wavefronts of light, fixed lenses are convenient, but often the need for frequent reshaping requires adaptive optical elements. There are a number of such active technologies, each with advantages and shortcomings. To overcome limitations such as speed and energy throughput for materials processing applications, we developed an adaptive optical element that we call a tunable acoustic gradient index of refraction lens, or TAG lens.
The spatial intensity distribution of a laser beam plays a crucial role in determining the light-matter interactions that occur. Nonetheless, users typically settle for whatever comes out of their laser — be it Gaussian or top hat — and use fixed lenses to produce a beam with the desired characteristics. In laser micromachining, for instance, a microscope objective will provide a sharply focused region of given area that provides sufficient power density to ablate the materials.
However, in a variety of applications, it is useful, even necessary, to have feedback between the beam properties of the incident light and the materials processes that are induced. A classical example is using a telescope to image distant objects through the atmosphere. In this case, the motion of the atmosphere causes constant perturbations in the wavefront of the light. One can measure the fluctuations and, using adaptive elements, adjust the wavefront to cancel out these effects.1 Other laboratory-based imaging applications, such as ophthalmologic scanning, confocal microscopy or multiphoton microscopy on living cells or tissue, would benefit greatly from the use of direct feedback to correct for wavefront aberrations induced by the sample under investigation.
Advanced materials processing applications also require precise beam intensity or wavefront profiles. In these applications, unlike imaging, one is modifying the properties of a material using the laser. For instance, laser forward-transfer techniques, including direct-write printing, can deposit complex patterns of materials — such as metal oxides for energy storage or even living cells for tissue engineering — onto substrates.2
In this method, a focused laser irradiates and propels a droplet of the material of interest mixed with a liquid toward a nearby substrate. The shape of the intensity profile of the incident laser plays a critical role in determining the properties of the deposited materials or the health of a transferred cell. In cases such as these, the ability to modify the shape of the incident beam is important, and the ability to change the shape rapidly adds increased functionality by varying the laser-induced changes in a material from one spot to another.
Even traditional laser processes such as welding or cutting can benefit from adaptive optical elements. In welding, a continuous-wave laser moves over a surface to create a weld bead between the two materials. Industrial reliability requires uniform weld beads, but slight fluctuations in the laser, the material or the thermal profile can diminish uniformity. Therefore, with feedback to an adaptive optical element, more consistent and regular features are possible.
Whether to process material or to create an image, the applications for adaptive optics are quite varied. Some require continuous-wave light, and others need pulsed light, but the unifying requirements are detailed control over the properties of the light and the ability to change those properties rapidly so that the overall process can be optimized.
Traditional adaptive optics
Fixed optical elements provide many choices for selecting the wavefront properties of a beam of light, but there exist few techniques for modifying the beam temporally. The simplest approach is to mount a lens or a series of lenses on motion-control stages; physically translating the elements deflects or defocuses the beam. This technique is useful for changing the focus of a beam to maintain imaging over a rough surface or for changing the spot size of a focused beam on a surface for laser micromachining.
However, the approach suffers from drawbacks related to large-scale motion such as vibrations, repeatability and resolution. It also can be slow and inconvenient for many industrial applications, where high reliability and speed are needed. Nonetheless, for certain applications, such as zoom lenses on security cameras, this is a satisfactory technique. More advanced methods of inducing mechanical changes to lenses involve electric fields or pressure gradients on fluids and liquid crystals to slowly vary the shape of an element, affecting its focal length.3
When most people think of adaptive optical elements, they think of two categories, digital micromirror arrays and spatial light modulators. The former is an array of small movable mirrors that can be individually addressed and that are usually fabricated with conventional MEMS techniques. The category also includes large single-surface mirrors that can be modified with an array of actuators beneath their surfaces. In either case, by controlling the angle of the reflecting surfaces, these devices modulate the wavefront and shape of light reflected from them. Originally, digital mirror arrays had only two positions for each mirror, but newer designs deliver a range of motion and angles.
Spatial light modulators also modify the wavefront of light incident on them, but they typically rely on an addressable array of liquid crystal material whose transmission or phase shift varies with electric field on each pixel.
Both digital mirror arrays and spatial light modulators have broad capabilities for modulating a beam of light, providing adaptive optical control. These digital technologies can faithfully reproduce arbitrary computer-generated patterns, subject only to the pixelation limitations. The devices have gained widespread use in many commercial imaging and projecting technologies; e.g., digital mirror arrays are commonly used in astronomical applications, and spatial light modulators have made a great impact on projection television and other display technology. On the research front, these devices have enabled a myriad of new experiments that rely on a shaped or changeable spatial pattern, such as optical manipulation or holography.
Although current adaptive optical technologies have been successful in many applications, they suffer from limitations that prevent their use under more extreme conditions. For instance, a major limitation of spatial light modulators is the slow switching speed, typically on the order of only 50 to 100 Hz. Digital mirror arrays can be faster, but their cost can be prohibitive.
Also, although these devices are good for small-scale applications, larger-scale devices require either larger pixels, leading to pixelation errors, or an untenable number of pixels to cover the area, decreasing the overall speed and significantly increasing the cost. Finally, these devices tend to have relatively low damage thresholds, making them suitable for imaging applications but less suitable for high-energy/high-power laser processing. These limitations and others can be overcome with the TAG lens.
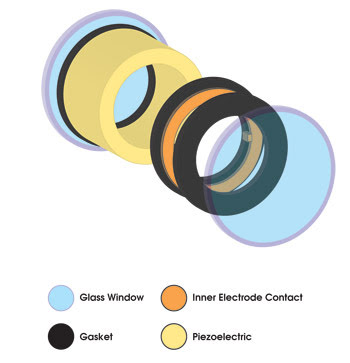
Figure 1. The simple design of a TAG lens makes it straightforward to fabricate.
Using sound to modulate
The TAG lens is a piezoelectrically driven device that uses sound waves to modulate the wavefront of an incident light beam. Its design is shown in Figure 1. Quite simply, the device is composed of a hollow piezoelectric chamber that is constrained by two glass windows on either side for optical access and filled with a refractive fluid.4
The lens works by creating a standing acoustic wave in the refractive liquid. The density variations in the standing wave result in refractive index variations that focus the light passing through the lens (Figure 2). The acoustic standing wave is created by an alternating voltage, typically in the radio-frequency range, applied to the piezoelectric element. The relationship of the drive frequency and the amplitude with the resulting refractive index modulation are nonlinear and complex, but they are predictable and can be numerically solved.5
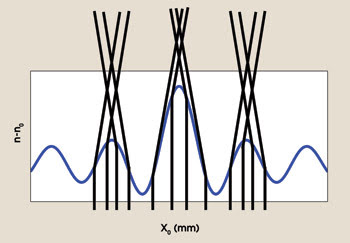
Figure 2. The blue curve is an index of refraction in a cylindrical TAG lens. Because of the acoustic wave in a cylindrical geometry, the index function itself is a zeroth-order Bessel function. As light enters this modulated-index field, it will be bent according to the local gradients.
Although the refractive index variation induced by the voltage is small, the lens is thick enough to allow significant focusing. Because the index variation is periodic, a TAG lens can not only shape a single beam of light but also take a single beam and create an array of smaller beams, as do other adaptive optical devices.
The optical properties of the lens are determined by a number of experimentally controllable variables. First and foremost, the geometry and symmetry of the lens determine the symmetries of the patterns that can be established. For instance, a square-shaped lens can produce a square array of beamlets, while a cylindrical geometry can produce Bessel-like patterns of light. The density and viscosity of the refractive fluid, the static filling pressure and the type of piezoelectric material all will play a role in determining the static and dynamic optical properties of the lens. These properties can be designed and optimized for different applications.


Figure 3. The intensity profile of a Bessel beam created by a TAG lens from a Gaussian input beam is the square of a zeroth-order Bessel function.
The frequency of the drive signal determines the location of the maxima and minima in the index function. Multiple driving frequencies and segmented piezoelectric elements can be used to give full functionality to this device to enable us to create arbitrary patterns.
Figure 3 shows a pattern created by a continuous-wave laser propagating through a cylindrical TAG lens whose piezoelectric actuator is driven by a sine wave. The figure shows that the incident Gaussian beam is reshaped into a central Bessel beam indicated by the concentric rings around the central intense spot surrounded by additional rings. Such patterns have important implications for laser micromachining or optical manipulation.6
Constant oscillation
An interesting feature of the lens is that, because it is driven by a radio-frequency signal, the index function is constantly oscillating at that frequency. For continuous-wave light, this oscillation is too fast to be significant, but with pulsed lasers, one can take advantage of the rapid index changes to produce different effects in sequential pulses. Figure 4 shows two of the instantaneous patterns that are created from the same driving parameters as those used for the continuous-wave beam of Figure 3.
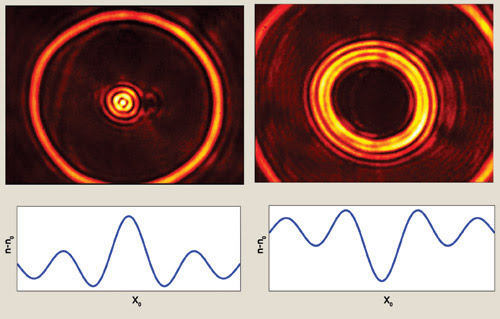
Figure 4. The intensity profile on the left results from the refractive index described by the blue curve underneath it. A moment later, the refractive index is described by the blue curve on the right, and the intensity profile on the right is created.
Although the other adaptive optical elements are digitally controlled, the TAG lens is an entirely analog device. It can reproduce complicated and arbitrary patterns, but with limitations that come from the symmetry of the device. The lens is not the best device for every job, but for some, it is just what is needed. Its advantages include scalability, high damage threshold, high-energy throughput, design flexibility, simplicity and low cost.
But one of its biggest advantages is its speed. In the digital adaptive optical devices, each pixel must be independently addressed and modified, a time-consuming task. In the TAG lens, the entire device is changed the moment a new sound wave propagates across the lens. This means that the minimum time for changing will depend on the speed of sound in the refractive fluid and on the size of the lens.
In reality, there are multiple time scales for the lens that depend on the tolerance for transients in a particular application.7 At the fastest level, these devices can change in microseconds, or at speeds of hundreds to thousands of kilohertz. In even more delicate situations, they are capable of kilohertz speeds, still significantly faster than the 10 to 100 Hz of many digital adaptive optical elements.
Because this lens is based on a refractive fluid, the damage threshold and energy throughput can be quite high. There is no need to worry about absorption in the lens material if the fluid is chosen appropriately for the wavelength. In fact, if the fluid or glass end plates do become accidentally damaged, a simple refilling operation or replacement of the glass plates can be performed in the field and will return the lens to new. This is a feature unique to the TAG lens.
The only required elements are a piezoelectric transducer, a filling fluid, two glass windows and a chassis, and the only component with significant associated cost is the piezoelectric transducer. Because all the components are macroscopic, no complicated techniques are required for assembly. When compared with the intricacies and expenses of other adaptive optical devices, the cost and ease of construction of a TAG lens are great advantages.
The lens can be made to any shape or size without affecting its control circuitry or operation, and the speed will scale linearly with the size, an important advantage for developing large-area devices. The lens can be filled and refilled with different refractive fluids, depending on the wavelengths of interest, the desired speed or other design considerations.
Further combinations of components are possible, such as curved end windows/lenses or multiple piezoelectric elements, providing additional design flexibility and functionality.
Meet the authors
Craig B. Arnold is an assistant professor of mechanical and aerospace engineering at Princeton University and is associated with the Princeton Institute for the Science and Technology of Materials in New Jersey; e-mail: cbarnold@princeton.edu.
Euan McLeod is a senior graduate student in the department of mechanical and aerospace engineering at Princeton University; e-mail: emcleod@princeton.edu.
References
1. A. Greenaway (2006). Adaptive optics: Astronomy and beyond. OPTICS AND PHOTONICS NEWS, Vol. 17, pp. 22-27.
2. C.B. Arnold et al (January 2007). Laser direct-write techniques for printing of complex materials. MRS BULLETIN, Vol. 32, pp. 23-31.
3. H. Jiang and L. Dong (Nov. 1, 2006). Smart lenses. PHYSICS WORLD, pp. 29-31.
4. E. McLeod et al (Nov. 1, 2006). Multiscale Bessel beams generated by a tunable acoustic gradient index of refraction lens. OPT LETT, Vol. 31, pp. 3155-3157.
5. E. McLeod and C.B. Arnold (Aug. 1, 2007). Mechanics and refractive power optimization of tunable acoustic gradient lenses. J APPL PHYS, Vol. 102, 033104.
6. V. Garcés-Chávez et al (Sept. 12, 2002). Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. NATURE, pp.145-147.
7. T. Tsai et al (Sept. 11, 2006). Generating Bessel beams with a tunable acoustic gradient index of refraction lens, PROC SPIE, Vol. 6326, 63261F.
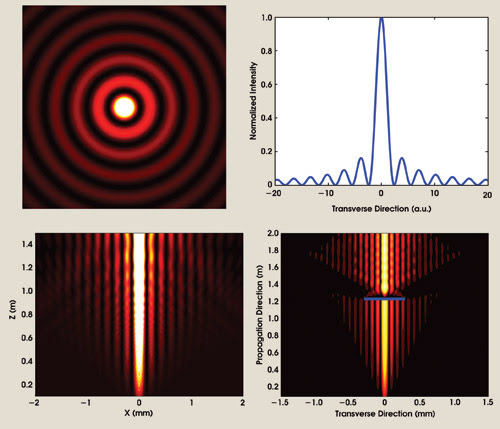
Bessel Beam
Bessel beam is one whose electric field is described by a Bessel function and whose intensity pattern is correspondingly described by the square of a Bessel function. The simplest case involves a zeroth-order Bessel function, which is the solution to Laplace's equation in cylindrical coordinates and which leads to the intensity profiles shown in the top two figures. Bessel beams have two special properties in comparison with Gaussian beams.
First, a Bessel beam represents a nondiffracting solution to the wave equation, which means that it can propagate over long distances without spreading out. The figure in the lower left demonstrates this point by plotting the intensity of a Bessel beam along the direction of propagation. The central region stays well-focused over large distances.
Second, Bessel beams exhibit self-healing behavior, which means that if they are blocked, they can re-create themselves farther downstream of the blockage. This point is demonstrated in the lower right image, in which a beam stop is placed in the beam path. Shortly after this blockage, the intensity pattern is re-formed, showing no shadow.
These properties make Bessel beams useful for optical manipulation and materials processing. The standard method to generate a Bessel beam is to use a conical lens with a small cone angle known as an axicon.