Dr. Kirat Singh, APNI Technology Corp., and Dr. Alan Streater, Boulder Optical Design Inc.
This approach enables not only wide-range tunable filters, but also an image demultiplexer that forms the core of a multispectral imaging system that captures high-resolution images in real time over a broad wavelength range.
Waveguide technology is the basis for a wide variety of optical devices, including filters and demultiplexers. Perhaps the simplest and most well-studied are planar waveguides, which are simply stacks of optical materials arranged in such a way that optical energy can flow along one or more of the layers. This can produce resonances in the structure that result in high transmission bands. A bandpass filter using this approach dates back at least to the work of Leurgans and Turner in the 1940s.1 Turner constructed an optical filter,2 but the rather poor material and deposition technology of the time resulted in low transmission.
Under certain conditions, the light can be treated as an infinite plane wave, and a standard thin-film model with frustrated total internal reflection predicts the optical properties. We will discuss extreme-range tunable bandpass filters based on coupled waveguide technology, and then an image demultiplexer, which can be used as the basis of an efficient spectral imaging system.
Some striking features of bandpass filters of this type are as follows: (a) very few layers and a relatively thin structure; (b) all dielectric materials with essentially no loss; (c) tremendous rejection ranges, where essentially all of the light is reflected; and (d) smooth, large rejection ranges, with especially strong rejection to the blue of the passband wavelength.
Tunable filters
The extremely broad rejection regions, without absorptive materials, can be exploited to design extreme-range tunable bandpass filters. An example of a tunable filter design that can be viewed in a dynamic web application3 covers a tuning range spanning two octaves (factor of four). Another feature of these structures is that the width can also be continuously tuned, and a filter can be made that is tunable in both peak transmission wavelength and width.
We have constructed a filter that demonstrates a wide tuning range and that is also tunable in bandwidth. The tuning range is about 400 to 1100 nm. In one test, we used two single-waveguide structures separated by a plate (Figure 1). More complex structures can be used for obtaining flatter passband regions and better rejections.
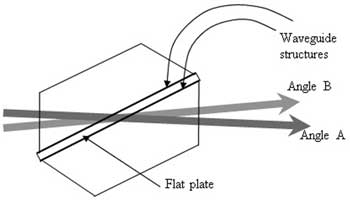
Figure 1. The wide-range tunable filter that was fabricated for the demonstration. Two angles of the incoming light are indicated. Different angles are achieved by rotating the prism relative to the incoming light. Vertical translations of the filter (in and out of the page here, not indicated) also tune the device because the waveguide structures are spatially varying.
The waveguide structures are spatially varying in the vertical direction (in and out of the page in the sketch above), and tuning is accomplished by vertical translation of the filter.
The transmission spectra for different vertical positions are shown in Figure 2 for two angular orientations relative to the incoming light, angle A and angle B, as indicated in Figure 1.
The small rise in the background in Figure 2a near 1100 nm is a spurious measurement artifact of the spectrometer. The absolute transmission levels were not accurate from these spectrometer measurements, so we normalized the curves. Independent laser measurements verify that the transmission levels through both waveguide structures are greater than 95 percent – and probably higher than 99 percent.
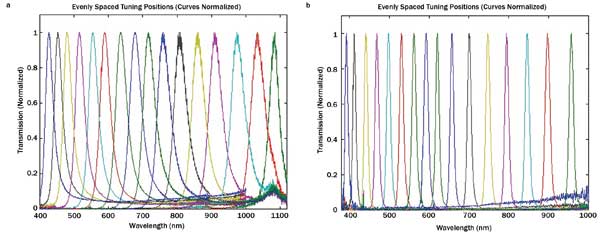
Figure 2. Transmission spectra for evenly spaced tuning positions, at two different angles: (a) angle A, and (b) angle B.
Figure 2b demonstrates that changing the angle has the effect of changing the width of the peaks as well as shifting the peak positions. The width alone can be tuned by rotating to change the width and peak, then translating to bring the peak back to the original wavelength.
Note that for a given tuning position (one of the curves in Figure 2), the rejections are better to the blue of the peak than to the red of the peak.
Multispectral camera
This same basic filter also can be the basis for a multispectral camera or image demultiplexer. To the basic filter structure we add reflection elements that provide for multiple bounces through the spatially varying waveguide structure. A separate image emerges for each wavelength channel.
The multiple reflections are arranged in such a way that the rejections are generally better than the single-pass transmission spectra shown in Figure 2a, particularly for wavelengths to the red of the channel wavelength.
As a first demonstration of the multispectral camera, we imaged a flashlight bulb filament through the device and showed the resulting images on white cards. Figure 3a shows a diagram of the experimental arrangement, and Figure 3b is a photograph showing the emerging beams on a white card.
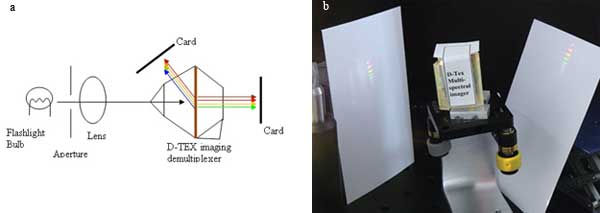
Figure 3. Demonstration of the image demultiplexer in the visible spectral region. (a) Sketch of the experimental setup. (b) Photo showing the emerging images in different wavelength bands.
To make a multispectral camera, we expanded the channels to cover a larger spectral range and replaced the white cards with camera sensors. We also used lenses to gather the images closer together, so that several images could fit onto each camera sensor. We used four camera sensors with four images on each sensor, for a total of 16 channels, covering the spectral range 420 to 1100 nm. The channel wavelength positions are similar to the peaks in Figure 2a.
To form the spectral image hypercube data set, we took subimages from the sensors. Figure 4 shows the multispectral image of the small flashlight bulb filament.
Channel 1 (ch1) is the longest-wavelength image, at about 1050 nm, and channel 16 (ch16) is the shortest-wavelength channel, at about 450 nm. The signals are weaker at long wavelengths because the sensor response is low for the longer wavelengths. The signals also are weaker at shorter wavelengths because the blackbody spectrum of the filament is weaker. Otherwise, the intensities for individual channels are not yet normalized to a calibrated white source.
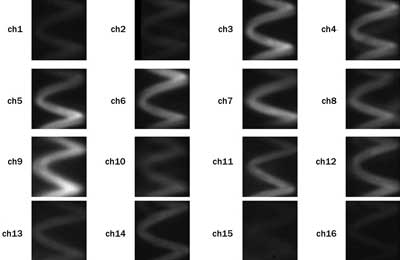
Figure 4. The image of a krypton flashlight filament, in 16 wavelength bands, with peak wavelengths from about 450 nm (ch16) to about 1050 nm (ch1).
This demonstration is configured as a microscope, and the resolution is about 4 µm. The optics in the demonstration system are crude; e.g., we used planoconvex lenses, and some channels are not in perfect focus because the path lengths for the different channels are not identical. Some ghost images were caused by imperfect angles in the reflection surfaces. Nevertheless, it clearly shows the viability of using the imaging demultiplexer as the heart of a multispectral imaging system.
Existing multispectral cameras can be divided into two broad categories: (a) lossy systems that waste incoming photons, and (b) nonlossy systems that do not waste incoming photons (assuming ideal optical elements). Lossy systems include filter-wheel systems, simple tunable filter systems, and common grating-based systems in which each frame images a different line from the object.
For example, a filter wheel or a simple tunable filter system wastes photons of the wavelengths that are not being transmitted through the filter for that frame. Typical grating systems waste photons from the objects that are not from the line that is being imaged for that frame (The photons are lost because they do not pass through the slit). Computed tomography imaging spectrometer systems and Fourier transform systems are nonlossy, but with both of these system types, a large numerical computation delays the presentation of the image, limiting the number of pixels that are practical.
This new multispectral imaging system is nonlossy and outputs unchanged wavefronts for all light channels simultaneously, and the images are immediately available on all channels.
Recall that we can tune both the width of the channels by rotation, and the peak transmission wavelengths by vertical translations. The channel spacing also can be tuned by adjusting the forward tilt of the device, enabling applications where such fine-tuning can improve the sensitivity to particular spectral features.
The width and translational tunings can increase the spectral resolution. First, we rotated the imaging demultiplexer to obtain narrowed channels (Figure 2b), then performed a short vertical translational scan to shift the peaks in Figure 2b slightly and record another frame. After a few frames, we filled in the gaps between the peaks in Figure 2b. For example, for a 16-channel system, taking three frames at three slightly different tuning positions produces a 48-channel spectral image at higher resolution.
This is a switch to a hyperspectral imaging mode, meaning higher-wavelength resolution. It does waste some of the light, passing only 33 percent of the photons, but it is not nearly as lossy as a system that images through a grating and a slit, which, for example, passes only 1 percent of the incoming photons if the system scans and images 100 horizontal lines.
A multispectral imaging system that is based on an imaging demultiplexer does not waste photons and is therefore good for low-light levels; it produces essentially instant results at video frame rates and has no moving parts.
The image demultiplexer described here, based on coupled waveguides, has adjustable channels in peak wavelength and width, is switchable between multispectral and hyperspectral modes, has good rejections (especially on the blue side of the channel) and smooth rejection curves, and has a simple structure with relatively thin layers.
Meet the authors
Dr. Kirat Singh has a PhD in physics from the University of Salford in the UK and is the CEO of APNI Technology Corp. in Edmonton, Alberta, Canada; email: [email protected]. Dr. Alan Streater, PhD, JILA/University of Colorado, is a scientific consultant and CEO of Boulder Optical Design Inc. in Boulder, Colo.; email: [email protected]. Both authors are working with the development team at Stream Technologies Inc. on this technology.
References
1. P. Leurgans and A.F. Turner (December 1947). Frustrated total reflection interference filters. J Opt Soc Am 37, p. 983 (A).
2. A.F. Turner (July 1950). Some current developments in multilayer optical films. J Phys Radium, Vol. 11, pp. 444-460.
3. http://www.boulderopticaldesign.com/extremerangetunablefilter.aspx.
4. F.D. van der Meer and S.M. Jong, eds. (2002). Imaging Spectrometry: Basic Principles and Prospective Applications, Series: Remote Sensing and Digital Image Processing. Springer, Vol. 4.
Applied technology
Applications for multispectral imaging are exploding.4 Because of good sensitivity and real-time results at video frame rates, the type of spectral imaging system described in this article is promising for relatively fast single-event applications. The sensitivity, adjustable channels and good rejection are also attractive for fluorescence and Raman applications. The simple structures and thin layers are attractive for systems in the infrared.
The extreme-range tunable filters also have other applications, including spectroscopy and beam cleanup.