Rüdiger Paschotta, RP Photonics Consulting GmbH
The operation of Q-switched lasers can be quantitatively understood – with huge benefits for laser design. In the September issue, we covered the operation and design of actively Q-switched lasers; this second part covers passively Q-switched lasers.
In a passively Q-switched laser, instead of an electrically controlled modulator, a saturable absorber is used. In its unsaturated state, it introduces a high optical loss. The laser gain must overcome that loss before lasing can start. When the laser radiation becomes stronger, it eventually saturates the losses – i.e., it reduces them to a much lower value. From this point on, the laser power rises rapidly until the gain is also saturated.
The power efficiency of a passively
Q-switched laser may seem inevitably poor because of the introduced absorption. But that is not true. If the saturation energy of the absorber is far below that of the laser gain medium, only a small fraction of the supplied energy is needed to make the absorber transparent. However, real absorbers often exhibit some amount of nonsaturable absorption, which does have an impact on efficiency.
Common saturable absorber materials are certain ion-doped crystals. For 1-µm lasers (e.g., Nd:YAG), Cr4+:YAG crystals are mainly used. As chromium ions integrate less well into YAG than neodymium ions, for example, and also exhibit various charge states, the quality of Cr:YAG is unfortunately more variable – particularly if high chromium concentrations are used. This means that choosing a low concentration is preferable, unless there is a clear necessity against it. Absorber crystals for other wavelengths are also available – for example, V3+:YAG for 1.3-µm lasers and Co2+:MgAl2O4 for 1.5-µm lasers. Typically, these absorber materials have a low saturation fluence (saturation energy per unit area), and their use in focused beams can further reduce the saturation energy (saturation fluence times beam area).
SESAMs (semiconductor saturable absorber mirrors) are another possible choice at various operation wavelengths. Here, however, the saturation fluence is typically three to four orders of magnitude below that of Nd:YAG. If the beam area is not made quite large, the SESAM easily gets into an oversaturated regime, where the device lifetime can suffer.
The pumping phase
For a passively Q-switched laser, the pumping phase lasts until the pulse buildup begins – i.e., until the net round-trip gain becomes slightly positive. That happens once a certain amount of energy has been stored in the gain medium. Note that the amount of stored energy at the time of pulse buildup does not depend on the pump power; for a higher pump power, this point is just reached earlier. Only the diameter and shape of the pump beam have some influence: The larger the pump diameter, the greater the energy that must be deposited until the pulse formation can start.
We can conclude that fluctuations of pump power will essentially translate into timing fluctuations but not into fluctuations of the pulse energy. This is profoundly different for actively Q-switched lasers, where both the pulse timing and energy are affected.
In numerical simulations, we usually treat pumping and pulse formation separately, as they happen on profoundly different timescales. Finding the end of the pumping phase can be a nontrivial issue for transverse multimode lasers, since the round-trip gain is generally mode-dependent, and modes may also be affected by gain guiding. Unless we have a clear-cut single-mode situation with negligible impact of gain guiding, we have to employ numerical beam propagation over several round trips with a suitable signal seed input.
Pulse buildup and absorber saturation
Pulse buildup begins once the net round-trip gain of the laser becomes slightly positive. Initially, the optical power rises only very slowly. Only when the absorber is becoming saturated will the net gain become substantially positive, reaching approximately the modulation depth of the absorber, or twice that value for an absorber in a linear resonator. The power will then rise rapidly toward its peak.
The pulse duration is essentially determined by the net round-trip gain in that phase and by the round-trip time, which depends on the resonator length. Typically, the pulse duration is about five times the round-trip time divided by the double-pass saturable loss.
Contrary to common beliefs, the saturation of a usual absorber is not linked to a certain intensity level, but is determined by the time-integrated intensity, called the fluence. A pulse with a duration far below the absorber’s recovery time (as usual) requires about one absorbed photon per absorber ion for complete saturation. The number of involved absorber ions is typically far lower than the number of excited laser-active ions, since the absorber has a lower saturation energy (so that a low absorbed energy causes a large change in absorption). Therefore, only a small fraction of the generated photons must be lost in the absorber, unless that also exhibits significant nonsaturable losses – which is, unfortunately, often the case. The nonsaturable (not useful) losses are often the dominant source of energy losses.
For a first rough estimate of obtained pulse parameters, the guidelines given above are sufficient. A more quantitative analysis, however, which can take into account various details of interest, requires numerical modeling. As an example, let us analyze a simple compact Q-switched laser based on a 10-mm-long Nd:YAG crystal and a 5-mm-long Cr:YAG absorber with 10 percent saturable loss and 3 percent nonsaturable loss. These are contained in a simple resonator as shown in Figure 1, with a curvature radius of 25 mm of the right mirror. The left mirror is a flat output coupler with 20 percent transmission. Resonator design software calculates a fundamental mode radius of 92 µm at the output coupler and 108 µm in the middle of the laser crystal.
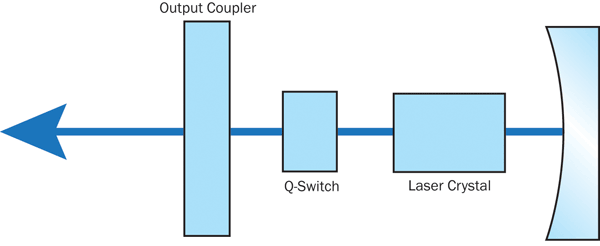 Figure 1. Setup of a simple passively Q-switched laser.
Figure 1. Setup of a simple passively Q-switched laser.
The Nd:YAG crystal has a saturation energy of 244 µJ (calculated with its mode radius), while the Cr:YAG crystal has only 7.6 µJ – mostly because of the higher transition cross section. As the start of the pulse generation requires a single-pass laser gain of 0.5 • 20% (output coupler) + 13% (absorber) = 23%, we need to store roughly 0.23 • 244 µJ = 56 µJ in the
crystal. A numerical beam propagation model actually tells us that 44 µJ is sufficient; this is because the assumed Gaussian pump profile (at 1 W and 100-µm beam radius) leads to higher gain on the beam axis, which counts more than the lower gain in the wings of the profile.
The temporal evolution in the pulse-generation phase is shown in Figure 2.
It leads to pulses with 22.4-µJ energy, 2.6-kW peak power and 7.4-ns duration. The pulse energy is only a little less than the decrease of stored energy in the laser crystal (23.6 µJ), since we use strong output coupling and an absorber with low saturation energy. The net gain is initially close to zero, then rises due to absorber saturation and finally falls by about twice its maximum value.
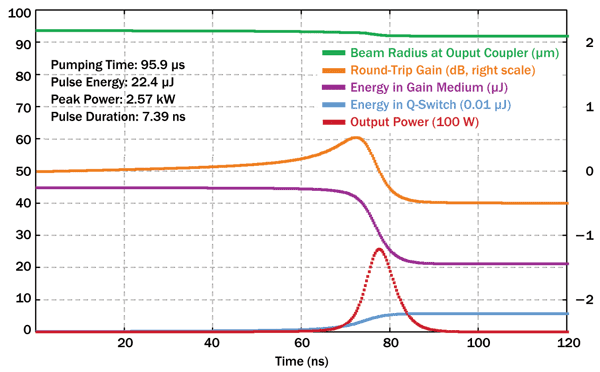 Figure 2. Simulated temporal evolution of various parameters during the pulse generation.
Figure 2. Simulated temporal evolution of various parameters during the pulse generation.
Despite the quite short resonator, the pulse duration is not that short, because the modulation depth of the absorber and thus the involved change of net gain is not very high. (Shorter pulses can be obtained with very compact microchip lasers, particularly when using a semiconductor absorber.) The beam radius is only slightly reduced during the pulse because of the change in gain guiding;
the relatively small resonator mode is rather robust against such influences. This is different in resonators with large mode areas, as required for much higher pulse energies; such devices are quite sensitive to thermal lensing and also to misalignment.
In simple models (ignoring the transverse profiles), the second pulse should have identical parameters. The more refined model, however, shows that the second pulse is somewhat more intense (at 25.7 µJ and 3.3 kW) and shorter (6.7 ns).
This is because the first pulse leaves some excitation energy left in the outer parts of the beam profile, so that the next pulse starts with an overall broader excitation profile (Figure 3). The second pulse is already close to the steady state. For high pump powers, resulting in high repetition rates, such effects are more pronounced. Also, the pump-beam profile has an influence.
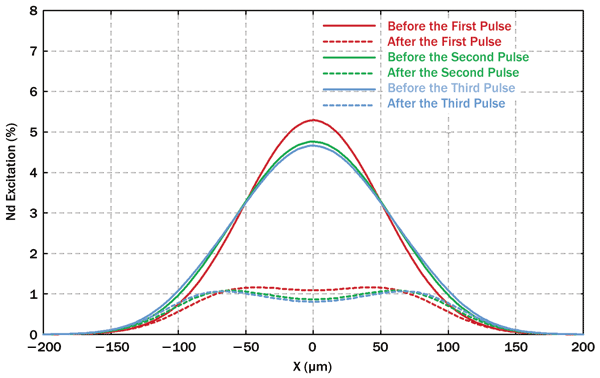 Figure 3. Transverse neodymium excitation profiles before and after the first few pulses.
Figure 3. Transverse neodymium excitation profiles before and after the first few pulses.
Pumping with 5 W instead of 1 W does not significantly change the pulse parameters; it only leads to higher pulse repetition rate (98 kHz instead of 15 kHz) for continuous pumping.
Complications in special regimes
Interesting effects can occur for a pump beam larger than the fundamental resonator mode. Higher-order modes may then come up – possibly leading to later-arriving pulses, as they have lower gain. Complicated dynamics involving instabilities can arise, also as a result of a misaligned pump beam.
Working with a rather small modulation depth of the absorber, or with absorbers having a longer excited-state lifetime, or with rather high pump intensities can lead to very high pulse-repetition rates. In that case, the absorber recovery between the pulses may be incomplete. That reduces the pulse energy and further increases the pulse repetition rate.
In general, although the basic operation parameters of a passively Q-switched laser can be estimated relatively easily, only a numerical model is suitable for investigating and optimizing various aspects of interest, such as the influence of the pump beam profile and its misalignment, gain guiding effects and possible instabilities that can occur under certain circumstances.
Meet the author
Dr. Rüdiger Paschotta is the founder and managing director of RP Photonics Consulting GmbH in Bad Dürrheim, Germany; email: [email protected]. He is also the developer of the RP Fiber Power software as used for the numerical simulations in this article.