Phase control has been an important component in optical design in applications using ultrashort pulse lasers and high-data-rate telecommunications lasers. Now, phase control requirements are emerging in life sciences applications such as structured illumination and multiphoton microscopy.
RANCE FORTENBERRY, PH.D., MIKE SCOBEY, PETER EGERTON AND AMBER CZAJKOWSKI, ALLUXA INC.
Thin-film filters (TFFs) can create virtually any spectral shape imaginable to modify the transmission or reflection of light in optical systems. During design, strong emphasis is often placed on optimizing the amplitude response, although for many emerging optics applications, equally important is the need to control the phase of the light. The frequently neglected phase response is increasingly a consideration for optical coating manufacturers, creating challenges that require new, sophisticated design and manufacturing methods.

Figure 1. Thin-film mirror stack reflection, amplitude and phase. QW = quarter wave.
It’s important to understand the basic physics of controlling both the phase and the transmission/reflection of TFFs. This information can then be applied to a variety of applications that employ high-performance filters to tackle difficult phase control requirements.
Based on the fundamental physics of optical interference, a thin-film filter consists of a stack of layers of varying index of refraction, each of which reflects and transmits light1. High-reflectivity (HR) dielectric mirrors (as opposed to metal mirrors with relatively low reflectivity) are Bragg reflectors constructed using stacks of layer pairs. As illustrated in Figure 1, each layer is a quarter-wavelength thick, and each pair consists of one layer of high-refractive-index material and one layer of a low-index material. If the layers are composed of dielectric materials, then it’s possible to achieve a reflectivity of >99.9 percent, limited only by scattering and material loss. The phase of light reflected from the mirror’s stack is often roughly determined by how deeply it penetrates into the thin-film stack before being reflected. This depth varies with wavelength (Figure 1), particularly if the mirror consists of multiple quarter-wave stacks optimized for different center wavelengths. The multiple-stack approach is often used to cover a single large wavelength range or multiple smaller ones.
The resulting phase delay varies with wavelength, resulting in group delay (GD), which also varies with wavelength, creating the group delay dispersion (GDD) of the mirror. Dispersion — whether low dispersion, fixed dispersion, dispersion compensating or even chirped — is often a simpler parameter to deal with, rather than working directly with phase. The performance of a simple low-dispersion mirror is shown in Figure 2, where the reflectivity is greater than 99.9 percent over a region of >100 nm, and the magnitude of the GDD is less than 80 fs2.
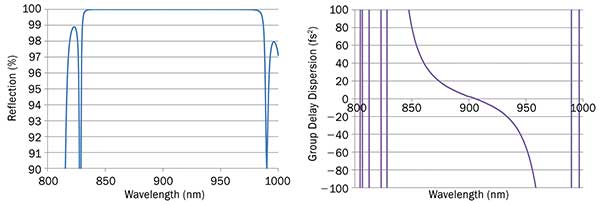
Figure 2. Amplitude and group delay dispersion (GDD) of typical single mirror stack.
A chirped mirror varies the layer thicknesses while going through the mirror stack to yield a roughly linear GD with wavelength. This approach allows the designer to produce mirrors in which the resulting GDD varies in a controlled manner with wavelength. By combining one chirped mirror with another designed to have the opposite GDD, total GDD can be controlled over a larger wavelength range than with a single low-dispersion mirror.
Short-pulse lasers
One of the first major applications requiring the full control of phase in thin-film dielectric mirrors and filters was the development of short-pulse lasers2. As these lasers gradually developed from pulse widths of nanoseconds to picoseconds, and then to femtoseconds and below, the phase requirements of thin-film components have become critical.
Continual improvements in design and coating capability help make short-pulse sources with pulse widths down to the attosecond regime feasible. One result is a recent increase in the wavelength range of low-dispersion mirrors, as seen in Figures 3 and 4. The first filter trades off maximum reflection efficiency for low GDD over an increased wavelength range from 800 to 1300 nm. The second maintains >99.5 percent reflection efficiency while achieving low GDD, from 700 to over 1000 nm.
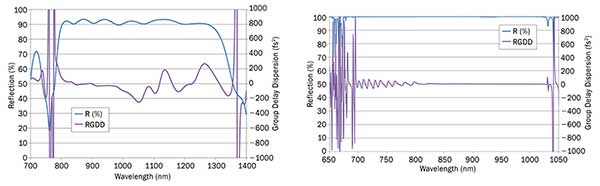
Figures 3 and 4. Wideband low-dispersion mirror coating examples.
Telecommunications
TFFs have been employed in optical fiber telecommunications since the beginning due to their advantages of high isolation, flat-top transmission shape, thermal stability and low cost.
A typical bandpass filter has a transmission profile (Figure 5). Bandpass filters are composed of two mirror stacks and a spacer that form a Fabry-Perot (FP) cavity. The cavity is then placed, coherently coupled, on top of n more cavities (where n = some arbitrary number) to achieve the desired spectral function. The thickness of the spacer determines the particular wavelength that is transmitted through the FP. The bandpass filter’s linewidth or wavelength profile is determined by the mirror reflectivity and the number of FP cavities.
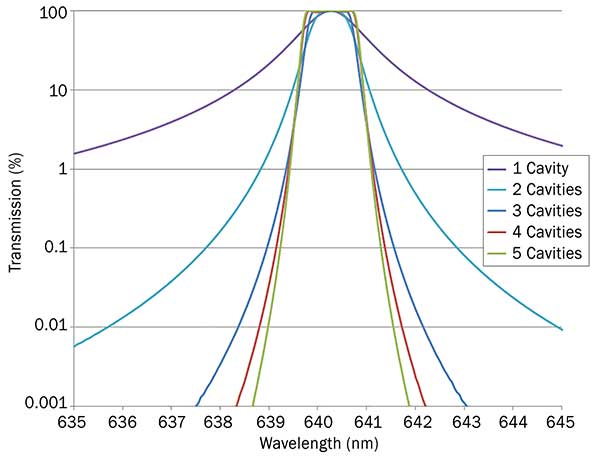
Figure 5. Typical variation in bandpass shape with number of cavities.
As expected, the phase of the transmitted wave is related to the time delay of the light passing through the filter. The delay is relatively small near the center wavelength of the bandpass, and increases to a maximum photon lifetime near the wavelength where the probability of transmission is 50 percent, or 3 dB down the filter slope. This results in the characteristic “bat ear” feature (Figure 6), which is common for GD profiles of thin-film bandpass filters. Since the dispersion is the change in GD with wavelength, it results in a roughly constant value of dispersion at the center of the filter. In the telecommunications field, this dispersion is called chromatic dispersion.
Phase for transmission filters
Thin-film reflective designs have greater flexibility in their phase response compared to thin-film transmissive designs. In transmission, a TFF is a minimum-phase infinite impulse response (IIR) filter3. IIR filters are limited by basic principles of causality and stability, such that the amplitude and phase responses are linked by a Hilbert transform. This becomes particularly important when using thin-film filters in telecommunications.
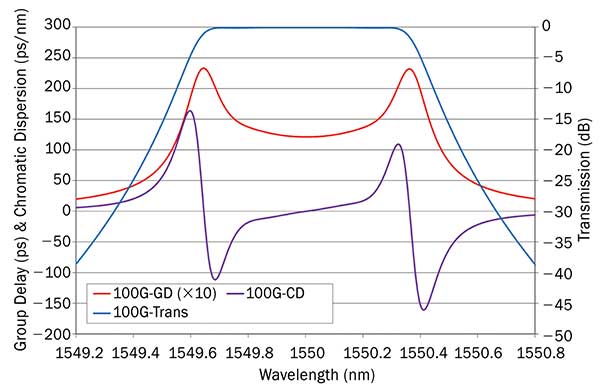
Figure 6. Group delay and chromatic disperson of a thin-film bandpass filter for 100-GHz channel spacing.
The phase variation in a bandpass filter is not readily adjustable by the filter designer, unlike the previous case of a simple mirror, mainly because the transmission amplitude and phase response are linked by a Hilbert transform. Any change the designer makes in the phase response immediately shows up in the amplitude response, and vice versa. This limitation applies to all light transmitted through thin-film filters but does not apply for reflected light, at least as long as the filter design is asymmetric3. For this reason, the phase response of a low-dispersion laser mirror can be adjusted nearly independently of its reflectivity, while the dispersion of the transmissive telecommunications filter is essentially fixed by the transmission amplitude itself.
Life sciences applications
Controlling the phase response of optical filters can also be critical to specialized bio-optics applications. For instance, phase contrast microscopy has used basic forms of phase filters dating back to the 1930s. In this case, the phase is determined by variations in the thickness of the filter, which acts as a waveplate having an annular variation in thickness across the field of view. In the case of polarization microscopy, systems are sensitive to coating-induced phase retardance, particularly those with high numerical aperture and thus large incident angles. This application often requires the thin-film antireflection coatings to be tuned such that the sum of the phase retardance for all the lenses is minimized4.
Superresolution microscopy has also helped to drive rapid developments in optical phase management technology. These measurement techniques allow the measurement and observation of features that are smaller than traditional diffraction-limited approaches. Two techniques that make use of the latest advancements in phase control are stimulated emission depletion (STED) microscopy and 3D structured illumination microscopy (SIM).
In STED, a version of multiphoton imaging microscopy, a phase filter is used to reshape one laser beam (the depletion beam) into a doughnut profile which then overlaps the excitation laser beam. Both beams are diffraction limited, but the depletion beam causes stimulated emission of the fluorescent molecules in the region where the beams overlap, leaving only the unilluminated central spot to fluoresce spontaneously. The beams are then mechanically scanned across the sample, producing a complete image of the fluorescence. The STED optical path is shown in Figure 7.
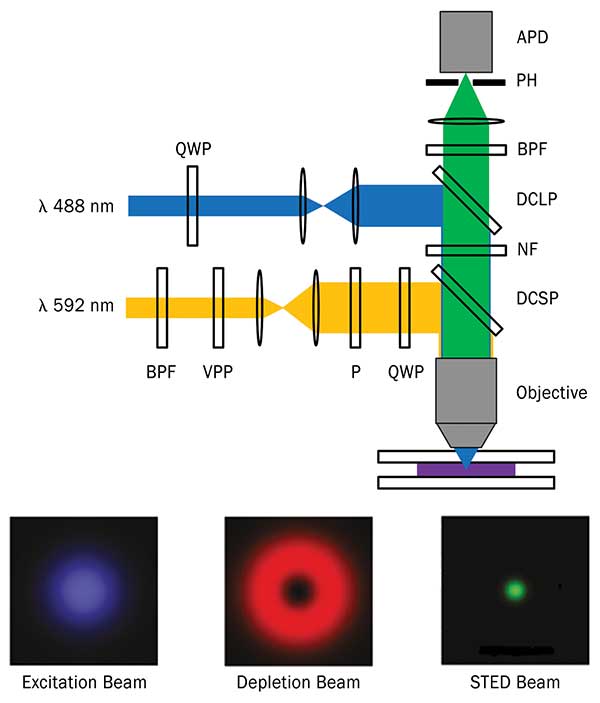
Figure 7. Layout of a CW-stimulated emission depletion (STED) microscope. Components include QWP (quarter-wave plate); BPF (bandpass filter); VPP (vortex phase plate); P (polarizer); DCSP (dichroic mirror short pass); DCLP (dichroic mirror long pass); NF (notch filter); PH (pinhole); APD (avalanche photodiode detector).
In the case of 3D SIM, the microscope creates a tetrahedral optical illumination structure where the location, phase and polarization are controlled using thin-film technology to take advantage of Moiré interference. The subdiffraction limit features can be reconstructed electronically by projecting this patterned light onto the sample and interpreting the resulting signal using complex algorithms.
Both STED and 3D SIM can provide superresolution imaging well below the diffraction limit of about 200-nm resolution, and have even been used to image single-molecule fluorescence. In the STED example above, there are eight thin-film components in the optical beams in addition to the vortex phase filter itself, thus demonstrating the demand for high-performance thin-film components in modern microscopy.
Thin-film filters are key components to today’s optical innovation, allowing the type and magnitude of light to be manipulated through a given path. Advancements in design techniques, as well as manufacturing capabilities to produce these state-of-the-art filters, have been key drivers in improving simultaneous control of phase and amplitude. From low-dispersion laser mirrors to bandpass filters used in fiber telecommunications and phase-maintaining and -manipulating filters for microscopy, recent TFF industry improvements have enhanced the design and manufacture of a variety of phase-sensitive systems.
Meet the authors
Rance Fortenberry, Ph.D., is the director of technology at Alluxa Inc. in Santa Rosa, Calif.; [email protected]. Mike Scobey is CEO of Alluxa; [email protected]. Peter Egerton is the executive vice president of business development at Alluxa; [email protected]. Amber Czajkowski is the product line manager at Alluxa; [email protected].
References
1. H.A. Macleod (2001). Thin-Film Optical Filters. London, U.K. Institute of Physics.
2. A.E. Siegman (1986). Lasers. Sausalito, Calif. University Science Books.
3. C.K. Madsen and J.H. Zhao (1999). Optical Filter Design and Analysis. Hoboken, N.J. John Wiley & Sons Inc.
4. R. Liang (2010). Optical Design for Biomedical Imaging. Bellingham, Wash. SPIE Press.