Advances in work materials and coatings are pushing this self-compensating mirror technology beyond traditional uses, such as laser tracking, and further into space-based interferometry, long-path spectroscopy and other emerging applications.
Zvi Bleier, Itai Vishnia and Jack Lipkins, PLX Inc.
Precision optical alignment capability across a range from the UV to the far-IR and a lighter-weight design have long given hollow retroreflectors an advantage over their solid cousins (retroreflector prisms) in boresighting, laser tracking, rangefinding, diverse laboratory applications and even space-based spectrometers. Within the past decade or so, enhanced work material and coating selection have expanded their application base into areas such as military and space-based atmospheric monitoring.
Solid or hollow, a retroflector is basically a self-compensating mirror that is completely insensitive to position and movement, such as tilt. Both configurations have three reflecting surfaces mutually connected at 90°. Parallel incident light entering the device will bounce three times against these surfaces and return to the source precisely at the same angle at which it entered the retroreflector — regardless of its physical orientation.

Figure 1. Hollow retroreflectors include three mutually orthogonal front surface mirrors bonded to form a corner cube. In many cases, a device will point at the light source such that each individual mirror surface tilts at a 55¼ angle of incidence to face it.
Commonalities aside, hollow retroreflectors offer several advantages over retroreflector prisms. Besides weight and cost advantages, the hollow design offers unparalleled accuracy. Depending on the application, an allowable beam deviation can range from 0.25 arc sec to minutes. These devices also have extremely low reflected wavefront error and do not face the problems with material absorption and achromatic aberration that are common with prism-type devices.
When mirror alignment to a light source of parallel beams is critical, a retroreflector frequently can eliminate the need for further alignment mechanisms, significantly contributing to system stability. Hollow devices could potentially replace flat mirrors in almost any application. The main characteristic that makes them attractive replacements is the invariance of the reflected beam with the tilt of the device. Each ray of a beam that fully illuminates and enters the component is translated proportionally to its distance from the center. Ultimately, though, the principal applications of these devices are those requiring front surface reflection. This usually means systems that operate at wavelengths that cannot be transmitted through glass prisms, such as applications in the UV and IR regions.
To fully understand the niche that hollow retroreflectors fill in optical alignment, it helps to examine their possible accuracy in greater detail.
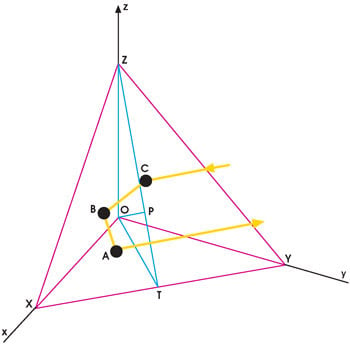
Figure 2. In a hollow retroreflector, the total length of the optical path is the sum of the lengths along which light bounces (AB and BC in this two-bounce illustration).
Exploring beam movement
When a beam enters a retroreflector, it creates an optical path with a total length defined by three bounces. This path depends on the location of the incoming beam with respect to the apex of the device. To better understand the process, it helps to examine an idealized situation with only two bounces. Consider a case where the retroreflector is essentially a roof mirror structure composed of two planes, OZX and OYX, where the vertex is OX and where a third mirror, the OZY plane, is perpendicular to the roof vertex OX. The optical path in this example is the length labeled AC (Figure 2).
Knowing the optical path has a great advantage in spectroscopy and interferometery applications where one must calculate the path difference. The following short-form equation, although it is based on a two-bounce analysis, also can help estimate optical path in a three-bounce situation (Figure 3):
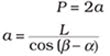
Where ß = angle of the incoming beam to the panel; a = angle of the outgoing beam to the panel/vertex; X1 = distance from the apex to the intersection of the outgoing beam with the retroreflector, measured in the direction of the outgoing beam; X2 = distance from the apex to the intersection of the incoming beam with the retroreflector, measured in the direction of the incoming beam; L = distance from the apex to the beam (incoming or outgoing) measured perpendicular to the beam direction; and P = optical path.
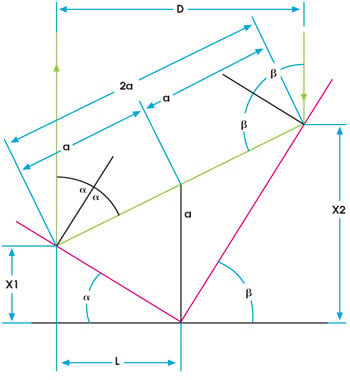
Figure 3. In this example used to illustrate short-form calculation of optical path based on a two-bounce analysis, the retroreflector axis of symmetry is perpendicular to the mounting plane. Typical parameters might include a = 35.2644°, ß = 90 – a.
If a pencil beam (one substantial-ly smaller than the clear aperture) enters the device, the offset generated by the inversion will be noticeable. Based on this offset between the incoming and outgoing beams, engineers can tweak system performance. The equations are as follows:
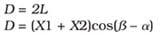
Where D equals the offset.
Traditionally, industry uses beam deviation as the key measure of accuracy. When a retroreflector is fully illuminated by a large parallel beam, it returns six subaperture beams. Accuracy is defined by the maximum deviation from perfect parallelism between the single incoming beam and the six outgoing beams. This can be verified with an interferometer (Figure 4).

Figure 4. A perfect retroreflector will have a perfect exiting wavefront, just like a perfect flat mirror. Interferometry can help illustrate device accuracy for a flat mirror (top) and a fully illuminated hollow retroreflector (bottom).
There also is a direct relationship between device accuracy and the error of the reflected, exiting wavefront, as shown by the following equation:
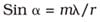
where λ = wavelength in millimeters, m = peak-to-valley wavefront distortion (one wave = one fringe), α = angular deviation in radians and r = radius of the clear aperture.
For example, when wavefront distortion is 0.25 waves and the hollow retroreflector’s clear-aperture radius is 15 mm and the wavelength equals 0.0006328 mm, the angular deviation would equal 2.1 arc sec.
Ultimately, the required device accuracy is application-dependent. For example, in optical, communications and laser systems demanding high precision, hollow retroreflectors can provide 0.25 arc sec of maximum beam deviation and 0.08 waves of wavefront deformation.
Typical standard hollow-retroreflector arrays for FTIR long-path spectroscopy might use individual 2.5-in. (63 mm) clear-aperture hollow retroreflectors with a maximum deviation of either 5.0 or 20.0 arc sec, although better than 1 arc sec is possible with custom arrangements. In this type of application, engineers mount the retroreflectors individually on an aluminum plate, placed very tightly together so that the array acts as a large, self-compensating mirror surface.
As another example, hollow retroreflectors better than 1 arc sec also are needed for high-resolution short-path FTIR applications.
Regardless of the rated accuracy of the retroreflector, proper mounting of the device to its interface is critical to eliminate any stress that has been induced on the mirror assembly and that could further distort the exiting wavefront.
One common method, the hard-mount, is used in applications where optical path difference is critical, such as with Michelson interferometers. The technique also is required when a ball-mounted retroreflector is used as a position target for laser trackers. In this application, engineers mount the compensating mirror device in a precision metal ball so that the device apex is at its center. This stability is critical because the tracker measures the distance between the apex and the center of its tripod to aid in its distance measurements.
It is important to bond the retroreflector to its interface using materials that cure to a very hard and stable substance. Vapor-cured materials such as silicon rubber should be avoided because of their inherent cold flow, which will cause constant change in the system position.
In a second technique, a soft-mount method used mainly in laboratories, the device is mounted in a housing and supported with a cushion of silicon rubber or other soft substance to protect it against handling shock during laboratory work.
Applications
Regardless of the application, selecting the right hollow retroreflector requires an understanding of the potential factors that could influence its accuracy, from mounting technique to required work material —most of which is still some form of glass — to the necessary coatings, which can range from metallics to dielectric materials. It is in these last two areas that retroreflector designs have seen key advances in the past five years. Applications benefiting in particular are those where devices must operate in harsh environments, such as in space or on battlefields. For instance, hollow-retroreflector-based technology provides boresighting of the fire control systems of the Apache helicopter.
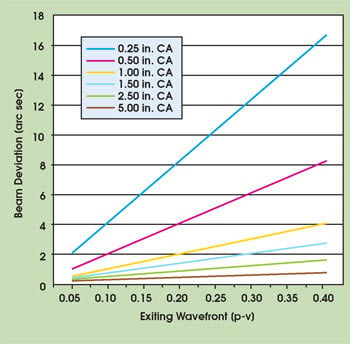
Figure 5. The relationship between exiting wavefront and beam deviation error differs for various retroreflector apertures.
PLX’s space heritage dates back to the 1970s when the company provided hollow retroreflectors to the Apollo-Soyuz Russian-American space hookup program. The devices measured gases in the environment of the vehicles. More recent projects include the Jet Propulsion Laboratory’s thermal emission spectrometer, which employs a hollow retroreflector assembly made of beryllium that provides a good ratio of density to stiffness and that is fairly stable at low temperatures. This instrument was designed to maintain 1-arc-sec accuracy at cryogenic temperatures after surviving launch vibration conditions.
Also, the Japanese space agency NASDA used a 50-cm-diameter Retroreflector in Space provided by the Japanese Environment Agency for atmospheric monitoring on its ADEOS satellite. This system, which also offered accuracy of 1 arc sec, contained a curved mirror to compensate for the movement of the satellite through space. PLX units also are being used in the European Space Agency’s Mars Express.
Meet the authors
Zvi Bleier is vice president and Jack Lipkins, CEO, at PLX Inc. in Deer Park, N.Y.
Senior Engineer Itai Vishnia is operations manager; e-mail: mailto:[email protected]