John M. Choi and Amnon Yariv, California Institute of Technology
In the pursuit of a large-area, high-power diode laser that maintains efficient single-mode operation, we have proposed a device that lases in a fundamentally different manner, the transverse Bragg resonance mode. To date, our work has focused on developing an accurate model of the device, and an experimental investigation is in progress.
The transverse Bragg resonance mode results from a unique approach to laser-cavity design. Rather than using lenses, mirrors or waveguides for transverse confinement, this function is provided by alternating index layers, resulting in Bragg resonant reflection. The closest analogies to the device are Bragg fibers, but the transverse Bragg resonance laser stems from a more general consideration: By introducing gain into the Bragg layer cladding, it is possible for the reflection to be greater than unity.
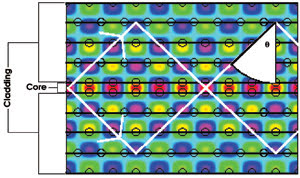
Figure 1. In this portion of a two-dimensional, finite difference time domain simulation of a transverse Bragg resonance waveguide mode, the Bragg cladding layers consist of a triangular-lattice configuration of airholes. The solid black lines show the planes of index contrast for an equivalent, one-dimensional Bragg stack. The core consists of the central portion, delineated by the two innermost rows of airholes, and the cladding extends on both sides. Note that the field distribution continues significantly outside the traditional core. The solid white lines show the direction and path of the two counterpropagating plane waves used in a coupled-mode analysis. The angle of incidence to calculate the effective length is shown (θ).
The transverse Bragg resonance waveguide consists of a core bordered on each side by a periodically varying medium, the Bragg layers (Figure 1). The exact geometry and symmetry of the periodicity is not important. A feature of a laser based on such a waveguide is the existence of a “phase matching” core section. Its role in the transverse direction is akin to that of the λ/4 phase shift in the longitudinal direction of distributed feedback lasers.
In the limit of a small index perturbation, the same limit as fiber Bragg gratings and distributed feedback lasers, we make the assumption that a transverse Bragg resonance mode consists of two counterpropagating plane waves in the transverse direction (the white paths in Figure 1), and we analyze their behavior using coupled-mode theory. The plane waves reflect off the Bragg claddings successively, resulting in a zigzag motion. These reflections are not due to total internal reflection, as in index guiding, but rather to the Bragg-resonant periodic scattering of the light.

Figure 2. In this scanning electron micrograph of an InP/InGaAsP/InGaAs transverse Bragg resonance waveguide, the core, or phase-matching defect, is the wide ridge in the center of the image. The surface grating provides an effective index modulation in the guiding region, which is several hundred nanometers below the surface. Confinement in the vertical direction is provided by traditional index confinement by designing the layers of epitaxial quaternary materials.
This scattering causes an oscillatory evanescence (complex exponential) behavior in the cladding, rather than the exponentially decaying tails associated with waveguiding (Figure 2). Consequently, the cladding transports a significant amount of energy, compared with the core. In the structures we have studied, the core may account for only 6 percent of the total energy, making it difficult to consider any core mode distinct from the cladding.
It is precisely this large mode, occupying both the core and the cladding, that gives a transverse Bragg resonance laser its advantage over conventional lasers for high-power applications. We calculate that the effective transverse modal width can be as much as 50 times that of a typical single-mode ridge-waveguide laser. As the index perturbation becomes smaller, the distance that the energy penetrates into the cladding increases. Thus, more layers are necessary to maintain high reflectivity, but this also means that the transverse Bragg resonance mode becomes broader.
Theoretical work also shows the feasibility of a quasi-single-mode design that takes advantage of the unique modal loss discrimination of the transverse Bragg resonance waveguide. The strong dependence of the Bragg reflection on frequency means that different propagating transverse modes can display large differences in propagation loss. Decreasing the index contrast to expand the mode also decreases the bandwidth of the Bragg reflection, so that fewer frequencies experience high reflectivity. This can be used to suppress higher-order transverse modes in larger-core transverse Bragg resonance waveguides that support multiple modes.
Another beneficial property of the transverse Bragg resonance waveguide is an enhancement of the gain for a given length. The Bragg cladding can be engineered to control the incident angle of the plane wave at the lasing wavelength. By decreasing the angle of incidence, the wave will bounce off the Bragg layers more often for the same axial length, producing more reflections per unit length. In a transverse Bragg resonance laser, the cladding also has gain (recall the greater-than-unity reflection). As a result, each reflection causes the wave to be amplified by the Bragg layers, and more reflections produce more gain.
Another way to understand the gain enhancement is that decreasing the angle of incidence causes the wave to zigzag more tightly, effectively folding the laser cavity between the two Bragg mirrors. Thus, the equivalent length of the laser cavity is longer, resulting in more gain given a constant gain per unit length. For an angle of incidence, θ, it is seen from geometrical arguments that the effective length increases by the factor 1/(sin θ), which is proportional to 1/β, the inverse of the propagation constant.
In sum, a larger distributed mode, the careful design of the transverse Bragg layers to reduce the number of supported low-loss modes, and the gain enhancement resulting from an effective cavity-folding scheme work together to extract the maximal optical energy from a given physical size of laser while maintaining efficient single-mode operation for desirable spatial beam characteristics and spectral properties.
Meet the authors
John M. Choi is a doctoral student and Amnon Yariv a professor at the California Institute of Technology in Pasadena; e-mail: [email protected] and [email protected].