This beam-steering technique is fast, accurate and relatively insensitive to vibration.
Craig Schwarze, Optra Inc.
With more and more applications requiring laser beams to be aimed at distant targets, such as for line-of-sight communications, aircraft-to-satellite secure communications, and laser weapons and countermeasures, there are increasing demands for compact, robust and economical devices for beam steering. Gimballed mirrors are the most commonly used beam-steering systems but, recently, Risley prisms are satisfying beam-steering requirements.
Risley prisms were originally used by ophthalmologists to measure binocular accommodation (the ability of the optical axes for the two eyes to converge for nearby objects) and thus had a relatively small angular range. More recently, they have been designed to cover a wide range of angles and have been achromatized to minimize chromatic variations in steering direction.
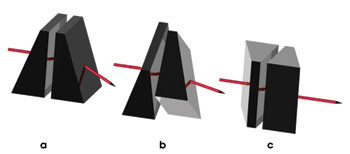
Figure 1. By separately rotating each of the prisms, an incident beam can be steered over a continuous range of directions.
Risley prisms work in pairs, with the two prisms oriented so that they refract light in the same direction and act as a single prism with twice the angle of either (Figure 1a). If each prism is rotated about the optical axis by the same angle but in opposite directions, the beam is deviated by a small amount but remains close to the plane defined by the optical axis and the refracted beam (Figure 1b). If the prisms are rotated 90°, they combine to act as a parallel plate with no net angular deviation (Figure 1c).
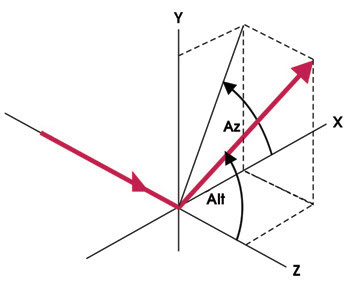
Figure 2. The altitude (Alt) is the angle of the beam relative to the optical axis, and the azimuth (Az) is the angle around that axis.
The angle of the beam relative to the optical axis can be called the beam’s altitude. The beam azimuth refers to the angle around the axis relative to a reference direction perpendicular to the axis (Figure 2). As the prisms rotate in opposite directions, they continuously deviate the beam from the maximum angle off-axis to zero, with little or no change in azimuth. To steer the beam to any specified altitude and azimuth, start with the prisms as shown in Figure 1b, rotate them in opposite directions until the desired altitude is achieved and then rotate them together about the axis until the desired azimuth is reached.
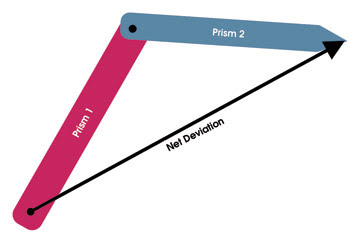
Figure 3. In this vector model of Risley prisms, the red vector represents the deviation of the beam created by the first prism, and the blue vector — which rotates about the end of the red vector — represents the action of the second prism. The end of the blue vector represents the net deviation produced by both prisms. Unequal lengths of the red and blue vectors would indicate that the prisms are not precisely matched — making a net deviation of zero unattainable.
Another way to view their action is to think of each prism as producing a vector deviation of an incident beam. The net deviation of the beam is the vector sum of the two separate deviation vectors. As each prism is rotated, the corresponding vector is also rotated (Figure 3).
The advantages of a Risley prism beam-steering system include compactness, relative insensitivity to vibration, low moment of inertia, independent rotational axes (no carried axes, no need for slip rings), robustness and speed.
 An obvious disadvantage is its inherent chromatic aberration; prisms, after all, are widely used by spectroscopists to disperse spectra. However, chromatic aberrations can be corrected in the same way that lenses can: by combining materials that have differing indices and dispersion characteristics. Optical engineers can design achromatic and apochromatic Risley prisms (using two or three materials) that minimize wavelength-dependent variations of beam-steering direction over relatively large spectral ranges. For narrow spectral bands, where the chromatic beam-steering errors are very nearly linear with wavelength, we have found that diffractive optical elements also do an excellent job of achromatization.
An obvious disadvantage is its inherent chromatic aberration; prisms, after all, are widely used by spectroscopists to disperse spectra. However, chromatic aberrations can be corrected in the same way that lenses can: by combining materials that have differing indices and dispersion characteristics. Optical engineers can design achromatic and apochromatic Risley prisms (using two or three materials) that minimize wavelength-dependent variations of beam-steering direction over relatively large spectral ranges. For narrow spectral bands, where the chromatic beam-steering errors are very nearly linear with wavelength, we have found that diffractive optical elements also do an excellent job of achromatization.
Extension to larger angles
For small prism angles, as the second prism is rotated about the optic axis, the steered beam travels in a circle about the direction in which the beam would have been steered by the first prism acting alone. Basically, each of the prisms acts independently to steer the beam by a fixed amount in a direction determined by the rotation of the prism about the optical axis.
This neat picture becomes less accurate as the prism angles are increased; the locus of the beam steered by the second prism is no longer a circle but becomes somewhat flattened in the vicinity of the maximum beam deflection. Moreover, as the angle of beam deflection increases, the cross section of the beam becomes elliptical, with the diameter reduced in the direction in which the beam is steered. This means that the diffraction spread is increased in this direction.
Standard optical design programs such as Zemax from Zemax Development Corp. of Bellevue, Wash., and Oslo from Lambda Research Corp. of Littleton, Mass., allow rays to be easily traced through pairs of Risley prisms in various configurations and allow the distortion of transmitted images to be readily assessed.
There are difficulties involved with steering beams in the immediate vicinity of the optical axis. If the two prisms are not precisely matched, it may not be possible to steer the beam along the axis without deviation. Even if they are precisely matched, large prism rotations (such as 180°) may be required to make very small changes in the beam-steering direction in the vicinity of zero beam deviation. This latter problem is particularly troublesome in tracking applications close to the axis. A simple solution is to insert a weak prism in the optical train when the steered beam approaches the nadir (zero deviation).
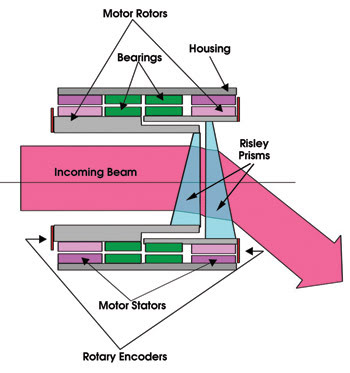
Figure 4. This schematic shows the key optical and mechanical components of a Risley beam-steering system.
Prism design
The optical design of a pair of Risley prisms is fairly straightforward. The second prism generally has to be somewhat larger than the first to accommodate the full beam diameter at maximum deviation. It is desirable to keep the adjacent faces of the two prisms parallel and normal to their common rotation axis; this tends to minimize the overall size of the prism pair. From a mechanical point of view, both prisms should have a common rotation axis.
The key elements of the mechanical design of a Risley beam-steering system are the two Risley prisms, two hollow-core brushless motors, two sets of bearings, two rotary encoders and a housing that defines a mechanical frame of reference (Figure 4).

Figure 5. Recently manufactured by Optra Inc. is a small Risley beam-steering system (a) that can steer a 3-mm-diameter laser beam over a full 120° cone angle and that is achromatized for the 2- to 5-μm spectral band. The company also makes a larger system (b) that has a 4-in. aperture and that can steer a diffraction-limited beam over the same angular range, with an aiming repeatability of better than 50 μrad (10 arc sec).
Risley prisms are providing a rapid and accurate means to steer optical beams over a wide range of angles, and in a variety of applications. Optra Inc. of Topsfield, Mass., recently developed a 3-mm-beam achromatic system for infrared countermeasures (Figure 5a) and a 4-in.-beam system for airborne laser communications (Figure 5b). The ability to separately rotate the two prisms about fixed axes allows for designs that are simple, compact and economical.
Meet the author
Craig Schwarze is a senior systems engineer at Optra Inc. in Topsfield, Mass., where he designs optoelectronic systems and manages R&D projects; e-mail: [email protected].