The technique couples precise computer-controlled motions with advanced software algorithms to provide full measurements of optical surfaces with either large clear apertures, high numerical apertures or both.
Andrew Kulawiec, PhD, QED Technologies, Rochester, N.Y., USA
Subaperture stitching interferometry (SSI®) has been proved to be an invaluable tool for today’s modern optics shop. Benefits include high spatial resolution and automatic calibration of reference wavefront errors. This method has been extended to the measurement of aspheric surfaces through the use of even more advanced stitching methods. Recent developments have increased the aspheric departure capability of this tool to more than 200 waves from best-fit sphere through the use of increased optical magnification and improved calibration algorithms.
Subaperture stitching was developed primarily to overcome the aperture size limitations of conventional interferometry. As the size of plano and convex optics increased, stitching interferometry became more attractive, in light of the time and expense of fabricating large-aperture interferometers and transmission spheres.
To address this need, QED Technologies developed the Subaperture Stitching Interferometer (SSI®), which became commercially available in 2004. In addition to the increased clear and numerical aperture capability, the SSI provides automatic in-line calibration of systematic errors — reference wave and distortion in particular. These capabilities enable measurements of large-aperture spheres with greater accuracy and less expense than are involved with a large interferometer with similarly large transmission spheres.
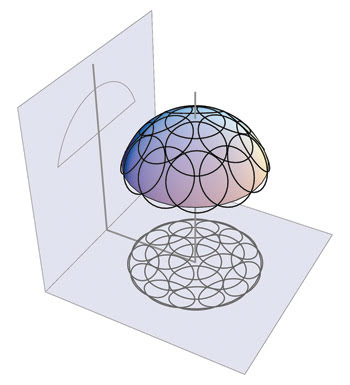
Figure 1. A “lattice” of subapertures covers the full aperture of high-numerical-aperture and large-clear-aperture parts.
The basic measurement principle of the SSI is shown in Figure 1. A large-aperture, high-numerical-aperture convex sphere is shown in the diagram. A standard transmission sphere in a Fizeau interferometer can measure only a small portion of the sphere, as indicated by each of the smaller rings, or subapertures. By creating a “lattice” of such subapertures that completely covers the surface of the sphere, a series of measurements can be performed and “stitched” together to obtain a full-aperture measurement of the sphere. Because the reference wavefront and imaging distortion errors of the interferometer are common to each subaperture, they can be solved for in the stitching process and subtracted from each subaperture prior to the final stitching. The results of this method have been proved to be more accurate than a measurement made by an equivalent large-aperture interferometer.
In 2007, QED extended the stitching process to include the measurement of aspheric surfaces up to approximately 100 waves of departure from best-fit sphere. This capability is made possible by measuring subapertures with a higher magnification than is necessary for simply covering the part. The aspheric departure is effectively divided into smaller portions with fringe patterns that can be resolved by the interferometer viewing system. Figure 2 shows a simulated fringe pattern of an asphere with approximately 50 μm (80 waves) of departure. Magnifying the subaperture and appropriately choosing the local best-fit sphere enable accurate measurement of the shape within the subaperture. The combination of an appropriate measurement lattice with the advanced stitching algorithms provides a full-aperture measurement of the asphere.

Figure 2. Simulated fringe patterns for the asphere prescription with ~50 μm of departure. The full aperture for a zonal null at 67 per cent of the aperture (a). Notice that data is not available over most of the aperture because the fringes become unresolvable. A magnified subaperture measurement allows many more of the fringes to be resolved (b). Choosing a local best-fit sphere further increases the resolvable region (c).
Increased aspheric departure
One factor limiting the aspheric measurement capability using the subaperture stitching process is the availability of longer-radius transmission spheres. The SSI uses standard 4- and 6-in. transmission spheres, which generally are available in a range from f/0.65 to about f/10. A transmission sphere with a larger f number results in a smaller subaperture on the part, thereby increasing the magnification and aspheric departure capability. However, custom-designed transmission spheres can be very expensive and require a long lead time to produce. Furthermore, a large f number transmission sphere results in a very long measurement cavity, often exceeding the available stage travel in the interferometer. The solution to this problem is to use an aperture converter in combination with smaller-aperture transmission spheres, as shown in Figure 3.

Figure 3. A 4× interferometer aperture converter (top) allows the use of the new smaller transmission spheres (bottom) to effectively double the range of aspheric departure that can be measured with subaperture stitching interferometry.
The aperture converter reduces the output beam of a 4-in. interferometer to 1 in., enabling the use of 1-in. aperture transmission spheres. These are relatively simple to design and, because of their small size, can be produced within a reasonable time and cost. Their use increases the range and departure of aspheres that can be measured with the subaperture stitching process. Furthermore, fundamental improvements have been made to the core stitching algorithms used in the measurement process, including more accurate calibration of systematic interferometer errors and the precise removal of part alignment errors. The combination of these two capabilities allows for the measurement of aspheres with more than 200 waves of aspheric departure. Manufacturers of high-precision optics now will be able to produce and measure an even greater variety of aspheres with high accuracy and resolution.
Contact: Jean-Pierre Lormeau; phone: +33 6 31 20 33 87; e-mail: [email protected].