Rüdiger, Paschotta, RP Photonics Consulting GmbH
Fiber amplifiers are in some respects ideal for amplifying short and ultrashort pulses. But serious limitations arise, particularly from nonlinearities, and many aspects must be checked for optimized amplifier systems designs.
In several respects, rare-earth-doped fibers appear to be the ideal gain media for amplifying short and ultrashort pulses. In the form of double-clad fibers, they can easily and efficiently turn over average powers of hundreds of watts or even more while preserving an excellent beam quality. They offer a large gain – easily 40 dB or even more in a single amplifier stage. For low-power preamplifier stages, they can have very high gain efficiencies, so that a large gain is achieved with a quite small pump power. In addition, the large amplification bandwidth of tens of nanometers (larger than for common laser crystals) allows the amplification of femtosecond pulses and gives the flexibility to amplify signals in a wide wavelength range.
Unfortunately, fibers also have disadvantages. In particular, serious limitations arise from nonlinear effects. Although silica, the base material for most optical fibers, has a particularly low nonlinear index, the combination of a relatively long length (particularly for double-clad fibers due to reduced pump absorption) and a rather small mode area leads to rather strong nonlinear effects: in particular, self-phase modulation, self-focusing, and stimulated Raman and Brillouin scattering. In some cases, limitations arise from amplified spontaneous emission (ASE) due to a high amplifier gain. With fibers, ASE can be increased both by a higher-than-desirable gain (due to the high gain efficiency) and by the quasi-three-level system of typical laser-active ions. In addition, there are various issues such as polarization – there are polarization-maintaining fibers, but these cannot always be used. The sensitivity of high-gain systems to optical feedback is another problem.
How limiting certain effects will be depends very much on the situation. In the following, we discuss some typical cases in very different parameter regimes.
Amplifiers for nanosecond pulses
Nanosecond pulses are required for many applications, including materials processing. Traditionally, they are generated with Q-switched bulk lasers, which easily generate few-nanosecond pulses with many millijoules; thus, with peak powers of megawatts or more. Fiber amplifiers present an interesting alternative: Offering a very high gain, they can be combined with low-power gain-switched laser diodes as seed sources. It is then easy to vary the pulse duration and repetition rate independently and in wide ranges, and even to use multiple seed lasers with different wavelengths; Q-switched lasers are much more limited in such respects. However, fiber lasers also have their limitations.
The peak power of a single-mode laser diode is usually limited to a few hundred milliwatts. A single-stage fiber amplifier with 40 dB takes that up to several kilowatts, implying only microjoule energies for nanosecond pulses. A second amplifier stage (after a bandpass filter against ASE) can in principle provide sufficient gain to get to the order of a megawatt and thus to millijoules, but various problems lurk in that regime. A hard limit arises from catastrophic self-focusing at peak powers of a couple of megawatts. Well before that, self-phase modulation can lead to severe effects, although not every application is sensitive to those. For narrowband light, stimulated Brillouin scattering is a very limiting factor. For a standard mode area of 100 µm2, the maximum acceptable Brillouin gain of ≈90 dB is already reached; e.g., for only 40 W over 1 m of fiber (for long-enough pulses). That limit can be strongly increased with a larger pulse bandwidth, but this is not easy to control with a laser diode alone.
Another limit arises from stimulated Raman scattering (SRS). Here, excessive power transfers to longer-wavelength components occur for roughly 10-kW peak power over a few meters. Fibers with larger-mode areas help to increase all these limits, except for the self-focusing limit.
Another issue is gain saturation. For example, an ytterbium-doped fiber for 1060 nm with a standard mode area of 100 µm2 has a saturation energy of ≈57 µJ. This means that output energies of a few hundred microjoules lead to a substantial reduction of gain during the pulse duration, which can lead to severe pulse distortions.
As an example, we consider a dual-stage Yb-doped amplifier for rectangular 100-ns pulses with 100-mW peak power at 1060 nm. For the first stage, we use a fiber with a small mode area of ≈80 µm2 to get a high gain with little pump power (500 mW). ASE limits the small-signal gain to ≈27 dB. The second stage, made with a double-clad fiber with a four-times-larger mode area, provides another ≈32-dB small-signal gain, also limited by ASE, with 5-W pump power in backward direction. Here, the ASE powers are increased as the core is slightly multimode, and ASE must be reduced with a bandpass filter (5-nm bandwidth) between the stages.
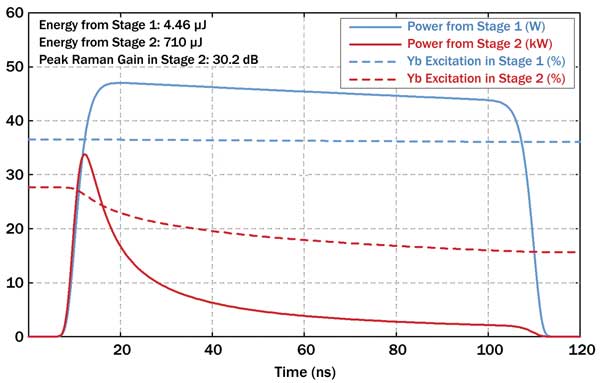
Figure 1. Amplification of nanosecond pulses in a two-stage fiber amplifier. Strong saturation effects distort the output pulse shape. The data resulted from a numerical simulation with the software RP Fiber Power.
Figure 1 shows the temporal evolution of the output power and the fractional Yb excitation in the two stages, assuming long pumping before pulse amplification. After the second stage, the pulse shape is strongly distorted by gain saturation. The calculated peak Raman gain in the second stage is 30 dB, which is acceptable. (For forward instead of backward pumping, it would be much higher – i.e., SRS would spoil the results.)
Figure 2 shows the same in the steady state for pulse amplification with a 10-kHz repetition rate. Here, the pulse energies are lower, mainly due to a lower gain in stage 2, where saturation effects are stronger. The pulse distortion is now weaker, and the Raman gain is much lower. The power loss via ASE (not shown) also becomes very weak.
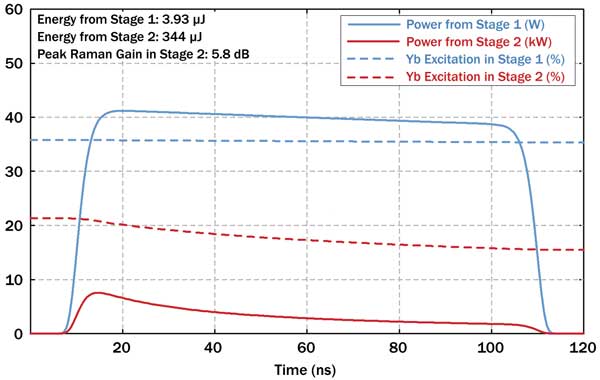
Figure 2. Same as Figure 1, but for the amplifier system in the steady state for operation at 10 kHz. The lower pulse energies reduce saturation effects.
The remaining pulse distortion could possibly be compensated with a suitable shape of the input pulses.
Obviously, a quantitative understanding of such amplifier systems requires numerical simulations, as effects including gain saturation, ASE and SRS complicate the operation details.
That understanding can then be the basis for systems designs that reach optimum performance without requiring unnecessarily expensive parts and long development times, as it would often result from a trial-and-error approach.
Picosecond, femtosecond pulses
For ultrashort pulses with picosecond or femtosecond durations, even moderate pulse energies are associated with huge peak powers. Even if critical self-focusing is avoided and SRS can be suppressed – e.g., by spectral filtering between amplifier stages – the combination of Kerr nonlinearity and chromatic dispersion can easily lead to severe pulse distortions or even complete pulse breakup.
Some techniques have been developed to cope with the strong nonlinear effects in this regime. A convenient method is amplification in the normal dispersion regime, where wave breaking can be avoided. Here, dispersion and nonlinearity pull the pulses toward an asymptotic solution with a parabolic temporal shape. The well-behaved optical spectrum allows for easy temporal compression – e.g., with a compact chirped volume Bragg grating. The pulse duration and bandwidth both grow in proportion to the cubic root of the pulse energy; higher energies thus lead to longer amplified pulses, but shorter compressed pulses.
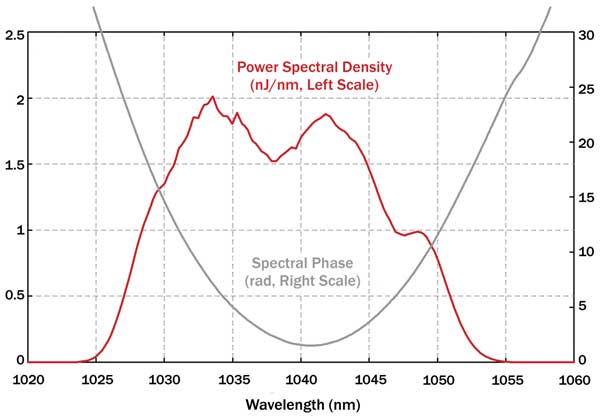
Figure 3. Power spectral density and spectral phase of a pulse after amplification in a two-stage fiber amplifier. Although the spectral shape and width are changed a lot with respect to those of the seed pulses, the parabolic spectral shape allows for easy dispersive pulse compression.
Unfortunately, there is only a limited scope for optimizing the pulse duration and bandwidth for a given pulse energy. As an example, consider the two-stage amplifier as above, now used for the amplification of femtosecond pulses. As the gain bandwidth limits the pulse bandwidth to a few tens of nanometers, the energy of parabolic pulses is limited to a few tens of nanojoules – far below the amplifier’s saturation energy, which is 113 µJ for the second stage. Therefore, a high average output power is possible only in combination with a high pulse repetition rate; e.g., of 100 MHz.
Figures 3 and 4 show the output pulses for a simulation with Gaussian input pulses, having 0.12 pJ at 1040 nm, 200-fs duration and 100-MHz repetition rate, as could be produced with a low-power mode-locked external-cavity diode laser. The originally 8-nm broad bandwidth is increased to 18 nm full width half maximum, and the pulse duration to 2.65 ps. The spectral phase is close to parabolic, allowing pulse compression to 130 fs with good pulse quality. Remarkably, the compressed pulses do not change much if the input pulse duration is two times higher or lower, or if the input pulses are chirped.
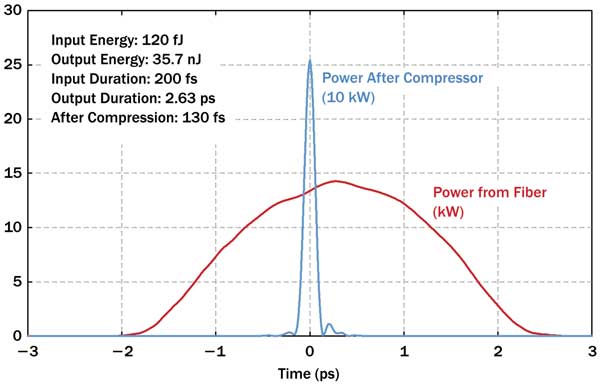
Figure 4. Red curve: the pulse of Figure 3 in the time domain. Blue curve: the pulse after compression with optimized second-order dispersion only. Its peak power is ≈250 kW.
Chirped-pulse amplification
Higher pulse energies require stronger temporal stretching of the pulses. The technique of chirped-pulse amplification implies strong dispersive pulse stretching before entering the fiber amplifier, and pulse compression after the amplifier. The longest practical stretched-pulse durations (with a bulky pair of diffracting gratings for compression) are a couple of nanoseconds, which, in combination with the self-focusing limit for the peak power (a few megawatts), leads to maximum pulse energies of the order of 10 mJ. Much more compact setups, which are also easier to align, are possible with volume Bragg gratings, but these offer much smaller stretched-pulse durations and, accordingly, lower pulse energies.
As substantial nonlinear effects occur despite the stretching, the compressor cannot simply undo the effect of the stretcher alone; the overall system must be optimized so that the compression works well. Again, numerical simulations are indispensable for checking various aspects, such as higher-order dispersion, nonlinear distortions, the limited gain bandwidth, gain saturation and ASE.
Application-specific decisions
As application demands in terms of pulse energy and duration, average power and pulse quality vary a lot, the most practical realization must be found in each concrete case. That may be a fiber amplifier system with one or several stages, possibly with additional parts such as filters and switches between the stages, pulse stretchers and compressors, and so on. In some cases, bulk solutions remain more practical and/or more powerful. Decisions on one of these technological pathways should be based on a careful analysis of a wide range of aspects. Numerical simulations are usually indispensable, since crucial performance aspects cannot be calculated with analytical means.
Generally, nonlinear limitations of fiber amplifiers are far more severe than those for the average power. Therefore, the advantages of fibers are best exploited for operation with high pulse repetition rates. For example, a 1-mJ chirped-pulse amplification fiber system might be operated at 100 kHz – i.e., with an average output power of 100 W.
Although a Ti:sapphire bulk system could easily offer much higher pulse energies, average powers well above 10 W are demanding for that technology. Fiber systems with hundreds of watts have been demonstrated already, and even the kilowatt regime is feasible.
Meet the author
Dr. Rüdiger Paschotta is the founder and president of RP Photonics Consulting GmbH in Bad Dürrheim, Germany; email: [email protected].