Vyacheslav M. Ryaboy, Newport Corporation, and Jerome Eichenberger, Polytec Inc.
Experimental results from a scanning laser Doppler vibrometer elucidate the effects of active vibration damping.
Vibration presents a major challenge for precision experiments and manufacturing processes in optoelectronics. Optical tables and breadboards in various shapes and forms are the de facto standard of vibration control. They rest on soft isolators that effectively filter out vibration from the floor. However, other sources of disturbance – acoustic noise, atmospheric turbulence and onboard sources – still exist and may become prevalent vibration sources at higher frequencies. These disturbances can have a significant negative impact on the optomechanical performance if their spectral contents are close to the resonance frequencies of the platform.

Figure 1. Optical breadboard with add-on active dampers prepared for laser Doppler vibrometer test.
For this reason, internal damping, or dissipation of mechanical energy, that mitigates the effect of resonance is very important for high-quality vibration-isolated platforms. Active vibration damping that involves electromechanical sensors, actuators and control systems has proved most effective for suppressing resonance vibrations.1,2 Recent extension of this technology by Newport with add-on SmartTable ADD active dampers expands the limits of applications beyond standard optical tables to virtually any vibration-isolated platform that can experience unwanted resonance vibrations.
The theory of active vibration control predicts that a small number of active dampers placed near antinodes of the main vibration modes suffice to suppress resonance vibration over the whole structure. In the case of a typical rectangular platform, two dampers placed at adjacent corners do the job. This has been confirmed by theoretical analysis and by multiple measurements of the dynamic reaction at remote locations on the table by highly sensitive seismic accelerometers.3 To illustrate this in a more vivid demonstration, researchers at Newport Corporation turned to the powerful experimental means provided by the scanning laser Doppler vibrometer from Polytec Inc. The experiment also promised valuable information about the proper tuning of the active control feedback loops.

Figure 2. In the test configuration, the laser head was attached to the gantry above the measured surface.
A custom all-steel optical breadboard was chosen for testing the effect of add-on active dampers (Figure 1). The breadboard, whose size was 4 ft × 5 ft × 4.5 in., was supported by four spring-based vibration isolators, so that the “rigid body” natural frequency of the suspension equaled 5.25 Hz. Two SmartTable ADD dampers were bolted onto the two front corners of the breadboard. To obtain a consistent stationary vibration signal, the breadboard was excited by a stationary random force. A miniature electromagnetic shaker was used for this purpose; it is seen at the far left corner of the breadboard in Figure 1.
The resulting vibration of the breadboard did not exceed the levels routinely observed in a laboratory environment, fitting to the VC-A vibration category (1⁄3-octave rms velocity below 50 µm/s).4 The signal from the force sensor, inserted between the shaker and the breadboard at the driving point, served as a reference signal for the laser vibrometer data processing. Finally, a lightweight low-noise accelerometer was installed near the shaker to perform a traditional dynamic compliance measurement in parallel with the laser vibrometer test.

Figure 3. The measured surface as seen by the Polytec software through the laser-head camera.
Scanning laser Doppler vibrometry enables vibration measurement at multiple points of the structure in quick succession, thereby allowing the researcher to estimate the kinetic energy of the whole structure. Reduction of the total kinetic energy is widely recognized as the criterion of vibration damping.5
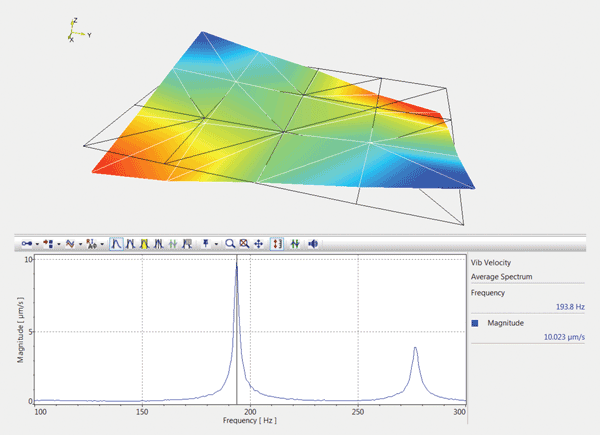
Figure 4a. Operational modes of the breadboard with damping turned off – first torsion mode at 194 Hz.
Polytec, which specializes in noncontact vibration measurements, provided its scanning laser vibrometer, PSV, to map the vibration of the breadboard. Scanning vibrometry is used for fast, accurate analysis and visualization of structural vibration for a wide number of applications. Laser vibrometry was well suited for this test and allowed measurements down to subnanometer excitation levels.
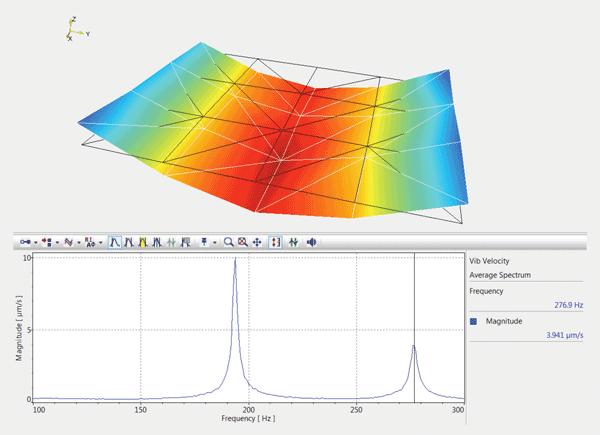
Figure 4b. Operational modes of the breadboard with damping turned off – first bending mode at 278 Hz.
Figure 2 shows the laser scanning head installed on a gantry system and prepared for measurement; Figure 3 shows the measured area as seen through the camera of the laser scanning head by the Polytec software. Twenty measurement points were distributed uniformly over the surface and equipped with reflectors. The full scan took only a few minutes.
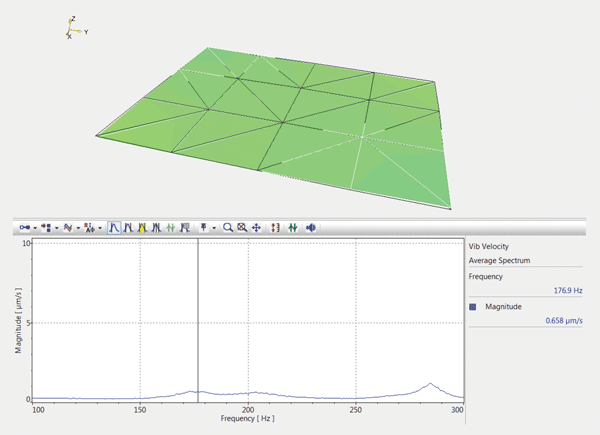
Figure 4c. Operational modes of the breadboard with damping turned on – first torsion mode at 177 Hz.
The results of the test provided a clear picture of the damping effect over the whole surface of the breadboard. Figures 4a-d depict the operational deflection shapes of the breadboard with active damping on and off.
Total kinetic energy is often considered the ultimate performance criterion for active vibration damping systems, and scanning laser vibrometry provides an effective tool for estimating this criterion. Figure 5 shows the contour charts of the square root of the mean velocity squared over the surface of the breadboard. The sum total of these mean squares is proportional to the estimate of the total kinetic energy. The spectral composition of that value is plotted, in rms units, in the graphs below. The comparison shows that the active damping practically eliminates both resonance peaks at 194 and 278 Hz, which correspond to the main twisting and bending vibration modes of the breadboard.
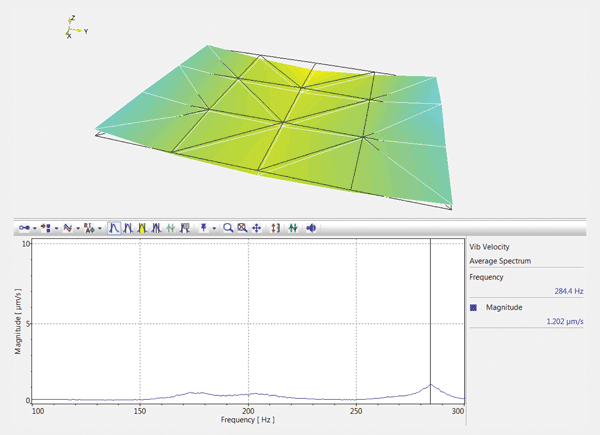
Figure 4d. Operational modes of the breadboard with damping turned on – first bending mode at 284 Hz.
The contour graphs of the undamped vibration shown in Figures 4a and 4b demonstrate the characteristic property of vibration-isolated platforms: The maximum vibration is reached at the corners of the platform. This is why active dampers are most effective when installed near the corners. The dampers placed at two corners effectively reduce vibration over the whole surface.
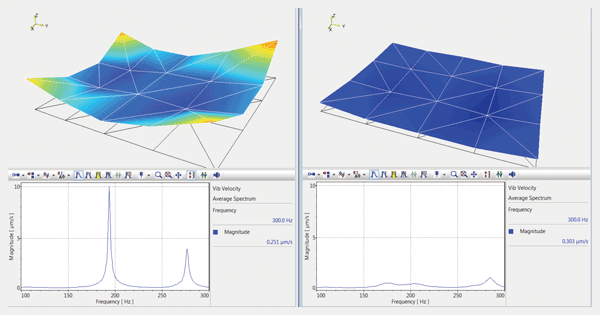
Figure 5. Reduction of the total kinetic energy of the breadboard by the active damping. The contour charts show the rms vibration velocity over the surface of the breadboard over the entire bandwidth of excitation. The graphs show the square root of the sum total of the velocities squared over all the measurement points. Left side: damping off; right side: damping on.
Besides the damper placement, another crucial consideration in active vibration damping is the choice of control functions and feedback gains. Decentralized velocity feedback has gained wide acceptance because of ease of implementation and (theoretical) unconditional stability.4 Practically, the useful range of feedback gains is limited by two factors: first, the “pinning” phenomenon, and second, the instability caused by frequency responses of the actuators and other elements of the control loops.6
To research the effect of ramping up the feedback gain on the global vibration control, vibration measurement with the scanning laser vibrometer was performed using the feedback gains below and above the gains recommended by the Newport multistep autotuning algorithm.3 For each level of gains, the sum of mean square velocities at all scanned points, which is proportional to the total kinetic energy, was calculated. The results are summarized in Figure 6. The autotuning process brought the system very close to the absolute minimum of the kinetic energy with a reasonable safety margin.
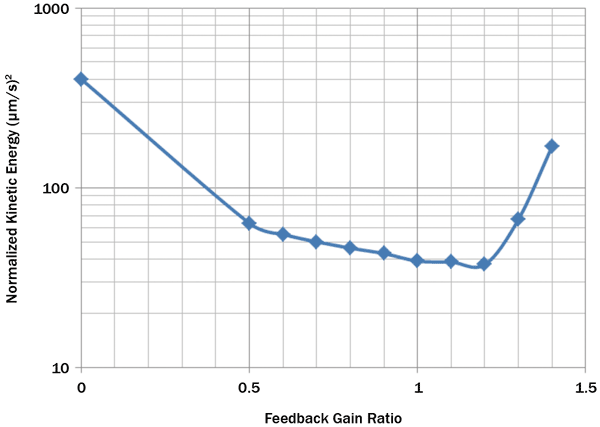
Figure 6. Feedback gain optimization. The sum total of mean velocities squared over all measurement points is plotted against the ratio of the feedback gains in both channels to the “autotune” values found by the SmartTable® algorithm.
The test confirmed that the active dampers are as effective applied to a custom isolated platform in “bolt-on” configuration as they are when embedded in standard tables: We observed fifteenfold reduction of the main resonance peak and tenfold reduction in the total kinetic energy. Scanning laser Doppler vibrometry enabled vivid illustration of the active damping performance.
Meet the authors
Dr. Vyacheslav M. “Slava” Ryaboy is principal mechanical engineer at Newport Corporation in Irvine, Calif.; email: [email protected]. Jerome Eichenberger is senior application engineer at Polytec Inc. in Irvine, Calif.; email: [email protected].
References
1. W. Booth (December 2006). Table improves optical systems from the ground up. Laser Focus World.
2. J. Fisher and V.M. Ryaboy (August 2008). Effective vibration reduction stabilizes laser beams. Laser Focus World.
3. V.M. Ryaboy et al (June 21, 2005). Optical table with embedded active vibration dampers (SmartTable). Proc SPIE, Vol. 5762.
4. H. Amick et al (September 2005). Evolving criteria for research facilities: I - vibration. Proc SPIE, Vol. 5933.
5. S.J. Elliott (2007). Global vibration control through local feedback. Adaptive Structures: Engineering Applications. David Wagg, ed. John Wiley & Sons, p. 59.
6. S.J. Elliott et al (2010). Self-tuning of local velocity feedback controllers to maximise power absorption. Recent Advances in Structural Dynamics: Proceedings of the X International Conference.