Frosted glass can extract light intensity and phase information from a single image without a reference light.
KYEOREH LEE and YONGKEUN PARK, KAIST
The term “holography” means a drawing that contains all the information of light — including its intensity and phase information. In contrast, photography only measures the intensity of light, and thus cannot address three-dimensional information that gives volumetric and depth perceptions. The missing information in photography is the wavefront (sometimes called complex amplitude or field information) of light, which describes the spatial latency or phase distribution of light. If one could take an image with the corresponding wavefront with a simple device, it would be an ideal form of holography and have great potential for various applications in imaging and display.
However, the insufficient temporal bandwidth of current electronics presents a fundamental challenge. The frequency of light at ~100 THz is several orders faster than the bandwidth of current, state-of-the-art electronics at ~100 GHz. This results in a phase problem, which has been a technical hurdle in numerous applications using electromagnetic waves.

Figure 1. Conventional speckle pattern snapshot. The spatial field distribution of well-diffused light is Gaussian random distribution, where corresponding intensity distribution is Rayleigh distribution. Courtesy of KyeoReh Lee, KAIST.
To remedy the issue, Dennis Gabor proposed a method that exploits interference of waves1. By recording an interference pattern between an unknown incident field and a known reference field, it is possible to retrieve the incident field information. Because of this powerful capability, reference-assisted holography has been utilized in numerous disciplines. Despite signi?cant efforts, however, the realizations and applications of holography have been limited because of the requirement of a well-defined known reference field.
Introducing a reference arm results in various limitations because it makes the system bulky, complex and vulnerable to ambient noise. Thus, it significantly limits the applicability of holography; holographic imaging systems had been built and operated on large anti-vibration tables in optical laboratories. Although several reference-free holographic methods have been proposed as alternatives, most of them have to sacrifice generality by assuming specific conditions about the incident light2; in other words, existing reference-free holographic methods can only be utilized in the specific situations.
Opaque glass causes speckle pattern
To solve this phase problem, Korea Advanced Institute of Science and Technology (KAIST) researchers proposed a different approach and decided to scramble the light using an optical diffuser. The light passing through the diffuser is diffused into a random pattern called a speckle pattern (Figure 1). This is generally true, except in very unusual situations where the wavefront of incident light is designed adaptively to diffusers3,4,5. Indeed, this random nature of a diffuser is not a desirable feature for imaging applications. Since a diffuser scrambles the input optical information, the image cannot be simply reconstructed from the diffused field. This is why diffusers are often called “opaque glass.”
Recently, Ivo Vellekoop and colleagues pointed out that the light passing through a diffuser is actually deterministic rather than random since the shape and internal structure of the diffuser are static<sup>3</sup>. In other words, there are certain input-output field relations of the diffuser that are like conventional optics. The input-output field relation is called a transmission matrix (TM) T, and it fully describes light transmission through a medium as
y = Tx, where x and y denote input and output field, respectively. Once the TM of a diffuser is measured, then the diffuser can be treated like a conventional optical component, such that light passing through the diffuser can be systematically controlled on demand. Since the TM of a diffuser is usually not designed on purpose, the calibration process should be utilized to determine the TM of a diffuser6.
Calibrating a TM is useful for imaging systems that include the inevitable diffusive obstacles such as air turbulence, biological tissue and multimode fibers. The input field reconstruction from the diffused field using the calibrated TM information has been demonstrated in the previous studies7. In such cases, since the TM is field-field relations, holographic techniques should be utilized to acquire the diffused field information. Indeed, in a conventional imaging system without diffusive obstructions, there were no reasons to introduce a diffuser that complicates the system, even if the TM of a diffuser can be calibrated.
Addressing the phase problem
Breaking with the conventional idea, the researchers utilized an optical diffuser as a key solution for the phase problem8 (Figure 2). A calibrated diffuser was installed in front of a camera that converts incident light into a speckle pattern. They showed that the incident field information could be directly retrieved from a single intensity speckle pattern without any additional requirements. Their work is counterintuitive because an optical diffuser is nothing but one of the diffractive optical components as in conventional lenses; and using a lens, it is impossible to reconstruct the incident field information from a single snapshot.
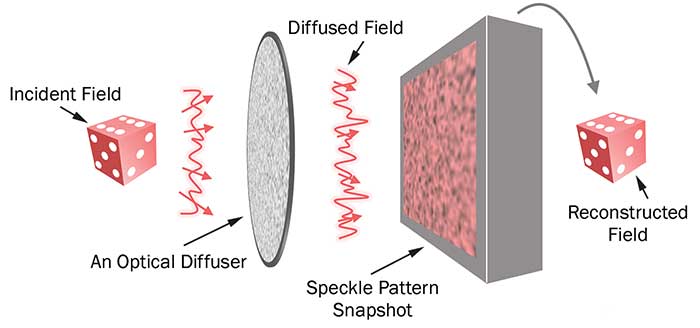
Figure 2. An optical diffuser as a holographic lens. The incident field is converted into the diffused field by the diffuser whose transmission matrix is known. Exploiting the random nature of the diffused field, the incident field can be reconstructed from the speckle intensity snapshot captured by a camera. Courtesy of Springer Nature.
The core of the proposed method is the random property of diffused light, which enables the utilization of a mathematical theorem (called Isserlis’ or Wick’s theorem) that connects the intensity correlations with field correlation of Gaussian random variables. According to Isserlis’ theorem, the randomized field should be correlated with the intensity information; in other words, the field information can be reconstructed from the intensity information.
Isserlis’ theorem is readily adaptable to the diffused field since the spatial field distribution of diffused light follows a complex Gaussian random distribution9. Using the theorem and the TM of a diffuser, the researchers established a novel holographic technique, called speckle-correlation scattering matrix (SSM) method, which only requires an intensity snapshot of a diffused field8.
One of the photonics devices that has utilized Isserlis’ theorem is a particle analyzer using dynamic light scattering — also known as photon correlation spectroscopy or quasi-elastic light scattering. A dynamic light scattering instrument measures time-dependent intensity signals of multiply scattered light from colloids. Employing the Siegert relation, a simplified version of Isserlis’ theorem, the field-field correlation of light scattering signals is obtained from the intensity-intensity correlation, from which size distributions or viscosity of colloids can be calculated. In fact, the proposed SSM method exploits Isserlis’ theorem for the spatial domain, whereas dynamic light scattering analyzes the time domain.

Figure 3. The photograph of the first demonstrated holographic camera using an optical diffuser (left). The optical diffuser is directly installed in front of the camera using common C-mount thread. The schematic shows the detailed composition of the system (right). The aperture and polarizer are added to block the ambient light. Courtesy of Springer Nature.
Simple and reference-free holographic image sensor
For their experimental demonstration, the researchers included a holographic camera that was constructed simply by attaching a commercial optical diffuser (ED1-C20, Thorlabs Inc.) in front of a regular CMOS camera (MD120MU-SY, Ximea GmbH) (Figure 3). An aperture and a polarizer were also used to block ambient light. After the TM calibration of the diffuser, the holographic camera was ready for use. As an operation test, incident fields were generated by using a spatial light modulator for phase modulation or a binary mask for amplitude modulation as targets. The demonstration generated incident fields, intensity snapshots and reconstructed fields (Figure 4).
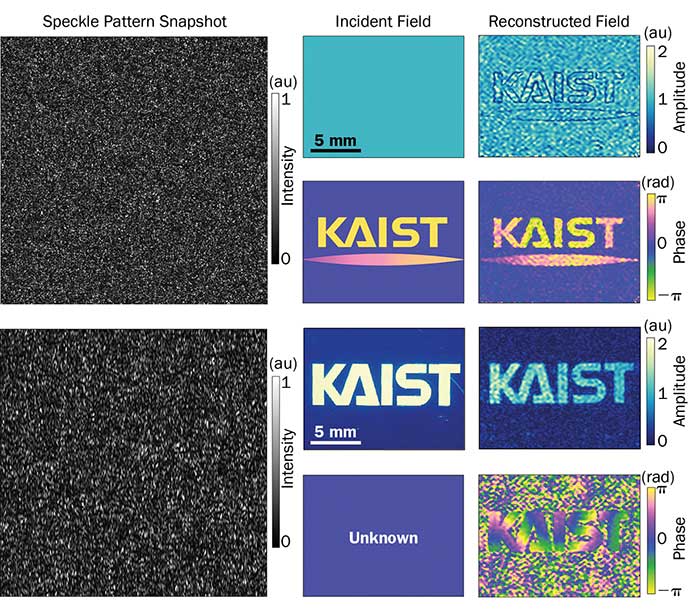
Figure 4. Using speckle-correlation scattering matrix (SSM), the incident fields are reconstructed from the captured intensity snapshot of the speckle pattern (left). The reconstructed field results (right) show good agreements with given incident fields (middle). Courtesy of Springer Nature.
To demonstrate the versatility of the method as a standalone 3D holographic camera, researchers also measured the volumetric 3D imaging of two dice. The dice were illuminated with coherent light while the holographic camera recorded the scattered fields. Using the proposed idea, the researchers reconstructed the scattered field information successfully; further, the researchers performed numerical refocusing based on the measured field (Figure 5). Since the dice have diffusive surfaces, the scattered light has a complex wavefront, which is not easily reconstructed using existing reference-free holographic techniques. Notice that the granular pattern on the diffusive surface is well-demonstrated as expected from the conventional holographic images of diffusive objects. For clearer visualization of the results, the researchers performed a conventional angular compounding technique. Reconstructed holograms in 25 slightly tilted laser illuminations were compounded into one clear image at each refocusing location (Figure 5).
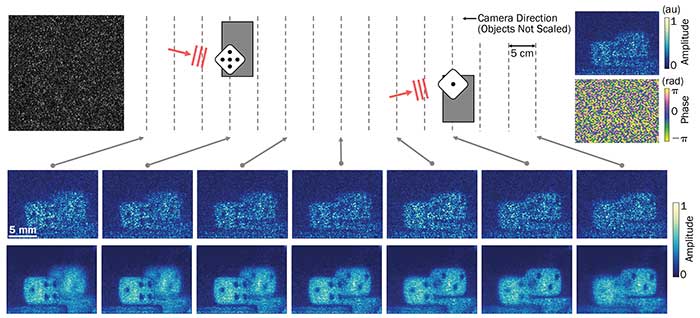
Figure 5. Diffused field retrieval. The reflected field from the diffusive surface of dice are reconstructed by the proposed method. Two dice are separated by 40 cm (upper middle). The measured intensity speckle image (upper left), and the corresponding reconstructed field result are shown (upper right). From the measured field result, the focal plane can be freely refocused for desired focal plane (lower part, first row). For clearer visualization, 25 holograms are compounded into one image (lower part, second row). Courtesy of Springer Nature.
This was the first demonstration of a standalone holographic camera that is simple, compact, reference-free, single-shot and assumption-less — just like a photographic camera. However, the proposed method still requires improvements. First, the TM calibration step required an interferometric setup, a time-consuming process. Though the TM calibration is only required once for each diffuser, configuring the interferometric setup would cause practical issues. This can be solved by using a faster and simpler configuration method. Alternatively, diffusers can be manufactured with sample surface properties, so that the same TM can be utilized for all diffusers. Second, calculation using TM information requires enormous computing power due to the massive size of a TM. The demonstrated TM was a 262,144 × 3960 complex single format matrix, which is about 5 GB in size. Since the hologram image quality is determined by the number of optical modes in the TM calibration step (3960 in these demonstrations), a larger TM is required for finer hologram image quality. Nevertheless, this problem could also be solved by the parallelization and optimization of computing processes.
This technology offers the advantage that hologram images can be measured with very simple devices. Using this feature, it would be possible to measure hologram images even in a device such as a smartphone. In addition, this technology can be a tailor-made solution, especially in the frequency domain where optical elements are limited, such as UV and x-rays, since light diffusers are always available in all frequency systems as long as light interacts with matter. The research was published in Nature Communications (doi: 10.1038/ncomms13359).
In addition, when the proposed concept is applied in a time-reversal manner, it can have applications in holographic display. Recently, the group also demonstrated that the use of holographic diffusers instead of a lens can significantly enhance the quality of holographic display; both the field of view and the image size of the 3D holographic display have been enhanced by greater than 2600 times10.
Meet the authors
KyeoReh Lee is a Ph.D. candidate in the physics department at KAIST, where he earned a B.S. Lee’s research interest is in wavefront shaping and imaging techniques; email: [email protected].
YongKeun (Paul) Park is associate professor of physics at KAIST. He earned a Ph.D. in medical science and medical engineering from Harvard-MIT Division of Health Sciences and Technology. Park’s area of research is digital holography and its applications for biology and medicine. To learn more about Park’s research projects, visit his website: http://bmol.kaist.ac.kr; email: [email protected].
References
1. D. Gabor (1948). A new microscopic principle. Nature, Vol. 161, Issue 4098, pp. 777-778.
2. J.R. Fienup (1982). Phase retrieval algorithms: a comparison. Appl Opt, Vol. 21, Issue 15, pp. 2758-2769.
3. I.M. Vellekoop et al. (2007). Focusing coherent light through opaque strongly scattering media. Opt Lett, Vol. 32, Issue 16, pp. 2309-2311.
4. A.P. Mosk et al. (2012). Controlling waves in space and time for imaging and focusing in complex media. Nat Photon, Vol. 6, Issue 5, pp. 283-292.
5. H. Yu et al. (2015). Recent advances in wavefront shaping techniques for biomedical applications. Curr Appl Phys, Vol. 15, Issue 5, pp. 632-641.
6. J. Yoon et al. (2015). Measuring optical transmission matrices by wavefront shaping. Opt Express, Vol. 23, Issue 8, pp. 10158-10167.
7. S. Popoff et al. (2010). Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys Rev Lett, Vol. 104, Issue 10, p. 100601.
8. K. Lee et al. (2016). Exploiting the speckle-correlation scattering matrix for a compact reference-free holographic image sensor. Nat Commun, Vol. 7, p. 13359.
9. J.W. Goodman (2015). Statistical Optics. 2nd ed. Hoboken, N.J.: John Wiley & Sons.
10. H. Yu et al. (2017). Ultrahigh-definition dynamic 3D holographic display by active control of volume speckle fields. Nat Photon, Vol. 11, Issue 3, pp. 186-192.