The ability to fabricate efficient and economic optical filters in laser-written 3-D waveguides has eluded researchers until now.
Haibin Zhang and Peter R. Herman, University of Toronto
Conventional optical waveguides are transparent structures, providing a refractive index contrast that guides optical fields via total internal reflection. Optical fiber is the best-known example, delivering light signals around the world while imposing losses of only a few tenths of a decibel per kilometer. Today, intense research is focused on building integrated photonic devices in which optical waveguides serve the vital function of connecting lasers, detectors, power splitters, filters and modulators. These devices have a myriad of applications, from communications and information processing to sensing and medical applications.
Planar lightwave circuits are crucial to the development of today’s photonics technology. They are two-dimensional photonic devices that integrate multiple optical functions on a single compact chip. Photolithography, which has matured under the microelectronics industry, is the technique commonly used today to fabricate planar lightwave circuits. The process involves complex multiple steps, including ultraviolet exposure, selective etching (chemical or plasma) and doping (ion exchange or diffusion) in a cleanroom environment. Despite its advantages in repeatability and in parallel processing, photolithography is a time-consuming, rigid multistep procedure that usually can produce only 2-D waveguide circuits.
More than a decade ago, Davis and co-workers first demonstrated with femtosecond lasers waveguide formation inside glasses.1 This development opened a new realm of opportunities for writing integrated optical devices directly inside bulk transparent materials. When laser pulses of ultrashort duration are focused onto an optical substrate, the normally transparent material becomes absorptive because of nonlinear processes,2 leading to a change in the refractive index of the material only at the intense focus point of the laser beam. Moving either the substrate or the laser beam forms a track of material with higher refractive index, thereby defining buried optical waveguides in all three dimensions.
Propagation losses in such waveguides have been reduced to below ~0.2 dB/cm in glasses, which is competitive with the ~0.02 dB/cm losses in modern, lithographically produced planar lightwave circuits. Compared with traditional photolithography, this direct laser-writing technology promises to be fast, maskless, flexible and relatively low in cost, while enabling novel architectures for designing a new generation of highly integrated and functional 3-D photonic circuits.
A rapidly expanding research community is pursuing advances in the technology of writing 3-D waveguides with ultrashort laser pulses. (See, for example, “ ‘Wiring’ Light with Femtosecond Laser Pulses,” Photonics Spectra, December 2004, p. 58.) Waveguides have been demonstrated in a broad range of materials, including various types of glasses,1,3,4 semiconductors5 and crystals.6
Additionally, numerous types of optical devices have been fabricated, such as waveguide amplifiers,7 wavelength converters8 and optical couplers.9
In the race to demonstrate these multifunctional 3-D optical circuits, one significant roadblock to commercialization has remained: For the past 10 years, embedding optical filtering devices in laser-formed waveguides has eluded researchers.
The Bragg grating waveguides developed in our laboratory provide a mechanism to integrate optical filtering into waveguides that have been written with femtosecond lasers. A Bragg grating waveguide is a normal waveguide with periodic perturbations of refractive index along the waveguide core. These perturbations form a one-dimensional photonic bandgap that reflects only a narrow spectrum from any broadband signal propagating along the waveguide.
Conceptually, Bragg grating waveguides are very similar to the familiar fiber Bragg gratings. Lasers have been used for nearly 30 years to fabricate fiber Bragg gratings, which function as narrowband mirrors integrated into optical fibers10,11 and which are commercially important for wavelength division multiplexing, for tunable filtering and — when chirped — for dispersion compensation in optical communications systems. Moreover, these devices are widely used in optical sensing because their resonant (reflected) wavelength is highly sensitive to environmental parameters such as temperature and strain.
In any Bragg reflector, the reflected wavelength, λB, is defined by the Bragg condition, λB = 2neffΛ, and is proportional to the waveguide’s effective refractive index (neff) and the grating periodicity (Λ). Because neff is close to 1.5 for most glass materials, a small grating period of approximately 500 nm is required for Bragg response in the telecom band near 1550 nm. Both UV10,11 and ultrafast lasers12 readily generate such finely patterned Bragg gratings in optical fibers by holographic or phase mask interference, or via point-by-point writing.13
Here, the pre-existing waveguide core, together with photosensitivity enhancement techniques (for example, rare-earth dopants or hydrogen soaking), facilitates strong laser responses for periodically modifying the waveguide refractive index across distances of about half a micron.
Is it feasible to use the same approach — optically writing a refractive index modulation into a pre-existing waveguide — to fabricate Bragg gratings in waveguides originally written with femtosecond lasers?
Until recently, only weak or high-order Bragg gratings had been reported for waveguides written into bulk transparent materials with ultrashort pulse lasers.14-16 One challenge is the overall weak photosensitivity response of most bulk glasses when applying traditional UV lasers to imprint Bragg gratings within such laser-formed waveguides. Even when using a femtosecond laser to modulate the refractive index in a second exposure step, one must overcome a photosensitivity response heavily saturated by the first laser-material interaction that wrote the waveguide core. Clearly, sequentially writing the waveguide core, then the index modulation required for the Bragg grating, is more complex and less likely to succeed than a single-exposure method would be.
Recently, our group demonstrated two single-exposure laser methods for writing strong Bragg grating waveguides in bulk glasses. The key here is to periodically lower the refractive index modification during the baseline high-intensity exposure that creates the waveguide but without diminishing the overall waveguide quality.
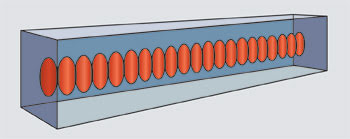
Figure 1. A Bragg grating waveguide is composed of an array of partially overlapped refractive index voxels created by a focused femtosecond laser.
Figure 1 is a conceptual image of such a segmented waveguide device. This Bragg grating waveguide is composed of an array of partially overlapping refractive index voxels (volume pixels) that contrasts sharply with conventional continuous laser-written waveguides. This new segmented waveguide structure of alternating pristine and laser-exposed volumes provides enough average refractive index change for efficient light guiding as well as sufficient refractive index modulation for strong Bragg resonances.
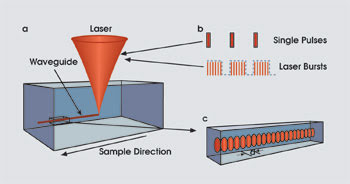
Figure 2. Smooth and continuous waveguides are formed by focusing an ultrafast laser beam to a small diameter (1 to 10 μm) inside a transparent sample (e.g., glass) undergoing relatively slow scanning (a). In the Bragg grating waveguide case, the individual voxels can be formed by single or multiple pulses at relatively fast speeds (b). In either case, the resulting waveguide provides low-loss guiding and high-strength Bragg resonance (c).
We fabricated such Bragg grating waveguides using two techniques: with pulses energetic enough to create each voxel with a single pulse or with multiple low-energy pulses to create each voxel. These two approaches are illustrated in Figure 2. In both cases, the ultrafast laser beam is focused to a small diameter (typically 1 to 10 μm) inside a transparent material (e.g., glass), and the sample is translated to form the array of refractive index modifications. For low-repetition-rate (1 kHz), ultrashort-pulse lasers widely available today, pulses of only several microjoules are sufficient to create a strong refractive index voxel with a single pulse. In this case, the period of the voxel array — that is, the wavelength reflected by the Bragg grating waveguide — is controlled by the scan speed and by the laser repetition rate.17
Alternatively, high-repetition-rate ultrafast lasers (≥100 kHz) typically have insufficient pulse energy to form a voxel in a single pulse, and bursts of laser pulses are required for sufficiently strong refractive index contrast. In this “burst writing” method,18 the grating period is controlled by the sample scan speed and the period between the bursts, while the refractive index contrast is controlled by the number of pulses in each burst.
We have demonstrated the single-pulse method in borosilicate glass with a low-repetition-rate (1 kHz) Ti:sapphire laser system made by Spectra-Physics of Mountain View, Calif., which provided 40-fs pulses of up to 1 mJ of energy at 800 nm.17 The light-material interaction is weaker in fused-silica glass, so to create Bragg grating waveguides in that material, we went to the burst method, using a frequency-doubled, high-repetition-rate ultrafast fiber laser manufactured by Imra America of Ann Arbor, Mich., that provided ~0.2-μJ pulses at 500 kHz and a 522-nm wavelength.18 In both cases, we obtained a voxel separation of 500 nm when we translated the sample at speeds of ~0.5 mm/s in the single-pulse method and at ~0.25 mm/s in the burst method. In the latter case, an acousto-optic modulator in the output of the fiber laser transmitted the bursts but blocked the beam between bursts.

Figure 3. The Bragg grating modulation of refractive index is not resolvable in the optical-microscope images of the waveguide fabricated by the single-pulse method (a) and the burst method (b). The mode profiles are of 1560-nm light emerging from each waveguide.
Figure 3 shows overhead microscope images of the two waveguides as well as the profiles of 1560-nm light emerging from each of them. The waveguides share a similar core-modification zone of ~2-μm diameter, but the ~500-nm periodic segmentation is not resolvable optically in these images. The guided optical mode profiles have similar diameters of ~12 μm, with the burst-written waveguide being slightly (~10 percent) larger. Both modes are nearly symmetric (aspect ratio ~1.1), and their intensity profiles are near-Gaussian, well-suited for coupling to standard telecommunication fiber. We measured the propagation losses in the two segmented waveguides at 0.5 and at 0.6 dB/cm for the single-pulse and pulse-burst waveguides, respectively.
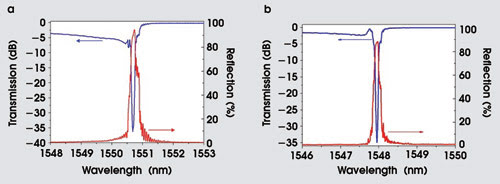
Figure 4. Transmission and reflection spectra of Bragg grating waveguides are written with the single-pulse method (a) and with the burst method (b) for borosilicate and fused-silica glasses, respectively. Grating lengths are 12 and 25 mm, respectively.
Figure 4 shows the transmission and reflection spectra recorded for a 12-mm-long, single-pulse waveguide and for a 25-mm-long, burst-method waveguide. Both samples show narrow ~0.2-nm bandwidths (measured at the 3-dB points) and strong ~35-dB reflections at Bragg wavelengths near 1550 nm. From these spectra, we infer a refractive index modulation of ~0.04 for the single-pulse waveguide and ~0.03 for the burst waveguide. The smaller index contrast in the burst case may arise from heat accumulation that extends and blurs in volume in which the index is modified. The reflection peaks of 95 and 90 percent for the two waveguides are sufficiently high for numerous applications in telecommunications, fiber lasers and optical sensing.
A significant advantage of writing Bragg waveguides with laser pulses is that optical characteristics — the grating strength, the bandwidth and the Bragg wavelength — can be adjusted easily simply by modifying the laser parameters and/or the translation rate of the sample. Tuning the optical characteristics of traditional fiber Bragg gratings is expensive and time-consuming, usually requiring a separate phase mask for each wavelength channel. As an example of this flexibility, Figure 5 illustrates the broad wavelength tunability that can be achieved with various scan speeds.
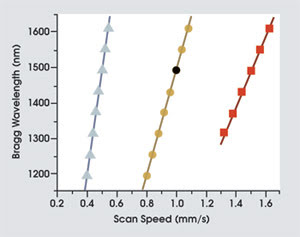
Figure 5. The filter wavelengths of Bragg grating waveguides are tuned simply by varying the scan speed. These data are for the first-, second- and third-order Bragg reflections of a waveguide fabricated in borosilicate glass with the single-pulse method.
It also is straightforward to integrate several Bragg grating waveguides into an optical circuit. Cascading multiwavelength Bragg grating waveguides can be carried out by changing the scan speed abruptly during laser exposure. When cascading fiber Bragg gratings, on the other hand, it is necessary to take multiple fabrication steps sequentially, each one requiring tedious alignment.
We implemented this speed-control method in writing a 50-mm-long grating in borosilicate glass. The grating had four 12.5-mm-long segments, each formed with a different scan speed: 0.5168, 0.5201, 0.5235 and 0.5268 mm/s. Figure 6 shows the spectra of this cascaded grating, where four distinct resonances are sharply defined both in reflection and in transmission. The fabrication time of this device was only ~2 min, dramatically undercutting the multiple time-consuming exposures required in the traditional phase mask method.
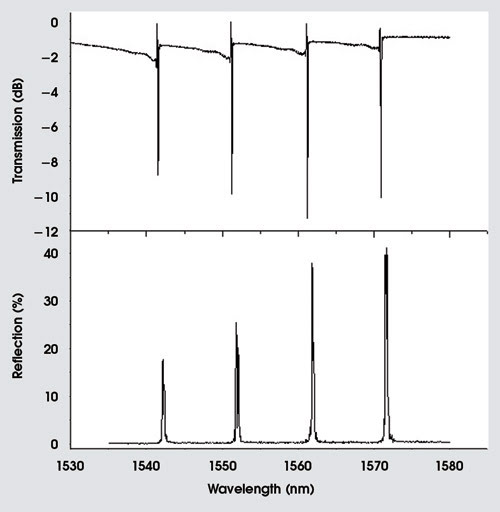
Figure 6. By varying the scan speed used to fabricate four sequential gratings in a single substrate, a filter with four different reflected wavelengths was produced.
This work shows that the basic building blocks for creating highly functional 3-D optical circuits are now in place. Two robust methods for laser-writing segmented waveguides have been demonstrated. Each method requires only a single exposure step to generate low-loss waveguides and high-strength Bragg responses simultaneously. Although such Bragg grating waveguide structures were demonstrated only in glass here, extension to other materials such as crystals, polymers, active glasses, nonlinear media and semiconductors is highly anticipated, promising the emergence of broadly based applications in optical sensing, spectral filtering and telecommunications systems.
Meet the author
Haibin Zhang is an applications development engineer at Imra America Inc.; e-mail: [email protected]. This work was done while he was pursuing his PhD at the University of Toronto’s department of electrical and computer engineering.
Peter R. Herman is a professor in the University of Toronto’s department of electrical and computer engineering; e-mail: [email protected].
References
1. K.M. Davis et al (November 1996). Writing waveguides in glass with a femtosecond laser. OPT LETT, pp. 1729-1731.
2. A.P. Joglekar et al (April 20, 2004). Optics at critical intensity: Applications to nanomorphing. PNAS, pp. 5856-5861.
3. K. Miura et al (Dec. 8, 1997). Photowritten optical waveguides in various glasses with ultrashort pulse laser. APPL PHYS LETT, pp. 3329-3331.
4. L. Shah et al (March 21, 2005). Waveguide writing in fused silica with a femtosecond fiber laser at 522 nm and 1 MHz repetition rate. OPT EXPRESS, pp. 1999-2006.
5. A.H. Nejadmalayeri et al (May 2005). Inscription of optical waveguides in crystalline silicon by mid-infrared femtosecond laser pulses. OPT LETT, pp. 964-966.
6. S. Nolte et al (June 18, 2002). Waveguides produced by ultra-short laser pulses inside glasses and crystals. In: Photon Processing in Microelectronics and Photonics (Proc. SPIE, Vol. 4637), pp. 188-196.
7. R. Osellame et al (July 1, 2003). Femtosecond writing of active optical waveguides with astigmatically shaped beams. J OPT SOC AM B, pp. 1559-1567.
8. J. Thomas et al (Oct. 8, 2007). Femtosecond laser-written quasi-phase-matched waveguides in lithium niobate. APPL PHYS LETT, Vol. 91, 151108.
9. A.M. Streltsov and N.F. Borrelli (Jan. 1, 2001). Fabrication and analysis of a directional coupler written in glass by nanojoule femtosecond laser pulses. OPT LETT, pp. 42-43.
10. K.O. Hill and G. Meltz (August 1997). Fiber Bragg grating technology fundamentals and overview. J LIGHTWAVE TECH, pp. 1263-1276.
11. R. Kashyap (1999). Fiber Bragg Gratings. Academic Press.
12. S.J. Mihailov et al (June 15, 2003). Fiber Bragg gratings made with a phase mask and 800-nm femtosecond radiation. OPT LETT, pp. 995-997.
13. E. Wikszak et al (2004). Recording of fiber Bragg gratings with femtosecond pulses using a “point by point” technique. In: Proceedings of Conference on Lasers and Electro-Optics (CLEO), Vol. 2.
14. M. Kamata and M. Obara (2005). Waveguide-based Bragg filters inside bulk glasses integrated by femtosecond laser processing. In: Conference on Lasers and Electro-Optics Europe (CLEO Europe), p. 492.
15. G.D. Marshall et al (2006). Direct laser written waveguide-Bragg gratings in bulk fused silica. OPT LETT, pp. 2690-2691.
16. J.-H. Chung et al (2007). Submicron-period waveguide Bragg gratings direct written by an 800-nm femtosecond oscillator. In: Conference on Lasers and Electro-Optics (CLEO).
17. H. Zhang et al (April 2, 2007). Type II high-strength Bragg grating waveguides photowritten with ultrashort laser pulses. OPT EXPRESS, pp. 4182-4191.
18. H. Zhang et al (Sept. 1, 2007). Single-step writing of Bragg grating waveguides in fused silica with an externally modulated femtosecond fiber laser. OPT LETT, pp. 2559-2561.