Ultrafast photonic integrated circuits could benefit next-generation optical communications systems.
Benjamin J. Eggleton, Vahid G. Ta’eed and Barry Luther-Davies, Centre for Ultrahigh-bandwidth Devices for Optical Systems
To operate at high bit rates of 160 Gb/s and beyond, optical communications systems must be able to process signals entirely in the optical domain, thereby overcoming the speed limitations associated with optoelectronic conversion. All-optical signal processing involves the control of light by light, which is possible only in a nonlinear optical material.
Before the adoption of wavelength division multiplexing (WDM) in the 1990s, the only means of expanding the bandwidth of an optical system was to increase its data rate. Therefore, twenty years ago a lot of effort was devoted to identifying optical materials with nonlinear properties suitable for all-optical processing. The advent of WDM delayed the push to all-optical processing, but the situation now has changed, and researchers are looking to process signals optically as a means of reducing not only the complexity but also the cost of high-capacity transmission systems.
Although many nonlinear optical materials have been studied — semiconductor optical amplifiers, nonlinear fiber, lithium niobate and, recently, silicon — no single platform yet stands out with regard to providing large ultrafast nonlinear response and low nonlinear absorption while allowing compact, easy-to-fabricate circuits.
Chalcogenide glass planar waveguides are a new contender in this race. These glasses meet the requirements for all-optical signal processing and already have led to a number of exciting results at Australia’s Centre for Ultrahigh-bandwidth Devices for Optical Systems (CUDOS), a research consortium consisting of the University of Sydney, Macquarie University, the University of Technology Sydney, Australian National University and Swinburne University of Technology.
Chalcogenide glasses
Chalcogenide glasses contain the chalcogen elements sulfur, selenium and tellurium combined with one or more elements, commonly germanium, silicon, phosphorous, arsenic and antimony. Their composition can vary widely, and this variation allows their optical and mechanical properties — refractive index, band-edge, nonlinearity — to be adjusted to suit a particular application.1,2
Chalcogenide glasses are primarily third-order nonlinear materials. At high optical intensities, nonlinear effects in a material’s response are generally described by a Taylor expansion. For isotropic materials, such as glasses, symmetry dictates that the lowest-order nonlinear process is of third order, and this gives rise to the optical Kerr effect — an intensity-dependent refractive index:
n = n0 + n2I
Here n0 and n2 are the linear and nonlinear (Kerr) refractive indices.
Miller’s rule, which is a semiempirical relation for predicting nonlinearity, implies that a high linear refractive index leads to large values of n2, as illustrated in Figure 1 with data for several glasses.3 Because chalcogenide glasses have rather large refractive indices, between 2 and 3, they exhibit a significantly larger n2 value than other glasses. Typically, their nonlinear refractive index in the telecommunications C-band (< 1550 nm) is two to three orders of magnitude greater than that of fused silica, the de facto standard.4
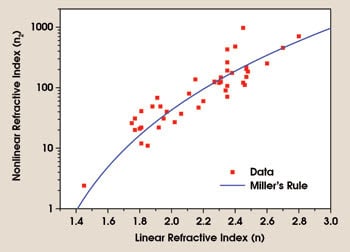
Figure 1. Miller’s rule predicts that the nonlinear refractive index (n2) increases with the linear index (n1). Shown here are experimental data for a number of different glasses, showing relatively good agreement with Miller’s rule.
Because the electronic bandgap of chalcogenide glasses lies in the visible or at the edge of the infrared, wavelengths in the C-band correspond to photon energies less than half the bandgap.5 (In amorphous media, the functional form of the density of states has two components: parabolic bands, similar to crystalline materials, and exponentially decaying tails caused by localized defect states.
The term bandgap, also called a Tauc gap, here refers to an extrapolation of the parabolic bands). The fact that the wavelengths in the C-band correspond to photon energies of less than half the bandgap has important consequences. First, because the photons are not resonant with any electronic transitions, the optical nonlinearities are caused by the bound electrons, which results in ultrafast response. For high-bit-rate optical communications (160 to 640 Gb/s per channel) this is critical because of the short pulse durations of 2 to 0.5 ps. Second, the low photon energy ensures that the chalcogenide glasses exhibit low or moderate two-photon absorption, a nonlinear process where two photons are simultaneously absorbed across the bandgap.
Two-photon absorption has been long recognized as a serious problem for all-optical signal processing,6 leading not only to a drop in device transmission but also to an increase in the optical power it dissipates.
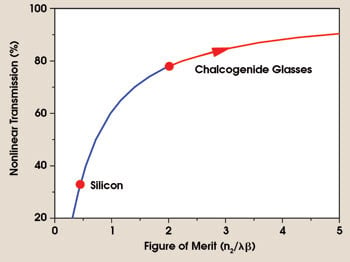
Figure 2. This plot shows the optical transmission for a device generating π radians of nonlinear phase shift as a function of the nonlinear figure of merit.
The suitability of a material for all-optical processing is characterized by a nonlinear figure of merit, T = n2/βλ where β is the two-photon absorption coefficient and λ the wavelength. Figure 2 shows the nonlinear transmission as a function of T. Chalcogenide glasses exhibit a T greater than 2 and more often greater than 10. Furthermore, in some materials, two-photon absorption results in the production of free carriers with long lifetimes,7 which slows the response time of the nonlinear interaction and limits its usefulness. Silicon is an example of a material with high two-photon absorption (T ≈ 0.4). The free carriers generated in silicon cause a large rise in the linear absorption, which is an additional problem.
Table 1 compares the nonlinear refractive index of chalcogenide glass with those of other common third-order nonlinear materials: bismuth oxide, silicon and silica. Chalcogenide glasses exhibit the highest nonlinear refractive indices and suffer, at worst, only moderately from two-photon absorption. Importantly, they do not suffer from free-carrier absorption.

Table 1. The nonlinear optical properties of several third-order nonlinear materials are compared.
A general characteristic of chalcogenide glasses is that they undergo photostructural changes when exposed to light near their bandgap. This results in relatively large changes to the optical properties, including the refractive index. Thus, similar to germanium-doped silica fiber, chalcogenides can be modified via their photosensitivity to fabricate integrated Bragg-grating filters.8 Figure 3 shows the transmission spectrum of a typical As2S3 waveguide Bragg grating inscribed using a Sagnac-based interferometer and green light. The Bragg grating shows excellent rejection and low side lobe structure.
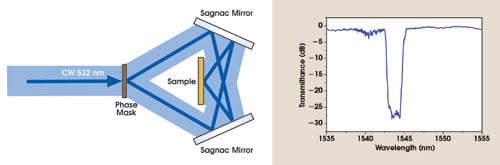
Figure 3. A modified Sagnac interferometer can be used to inscribe Bragg gratings into As2S3 waveguides (left). The transmission through an As2S3 waveguide grating is highly selective (right).
Chalcogenide glasses do suffer from some issues related to stability and aging. Although mechanically weaker than silica-based glasses, their compositions are stable. Note that the US Naval Research Laboratory has been working with these glasses for many years.9 The optical damage mechanisms are not well understood, although certain compositions do offer greater resistance than others. We have, however, operated As2S3 chalcogenide glass planar waveguides stably at 1550 nm at continuous average intensities of more than 6 MW/cm2, as well as peak pulse intensities of ~1 GW/cm2, which is more than sufficient for most applications.
Being glasses, the chalcogenides are a versatile platform for making not only optical fiber but also planar waveguides. Such waveguides have progressed rapidly, and we routinely produce low-loss, strongly confined designs by applying relatively standard photolithography and dry etching to films produced by pulsed laser deposition.10 Figure 4 shows the cross section of a typical As2S3 chalcogenide rib waveguide with a mode area of ~5 μm2, which strongly confines the optical field and enhances the nonlinear response. Using these waveguides, we have demonstrated several functions required for all-optical signal processing. In this article we will discuss two of them: wavelength conversion and all-optical signal regeneration.
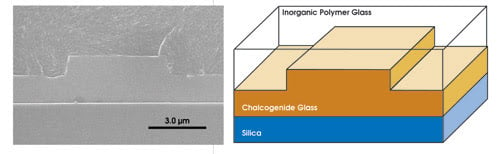
Figure 4. A scanning electron micrograph shows the cross section of an As2S3 chalcogenide glass rib waveguide not yet fully etched into a channel (left). A schematic clearly shows the device’s components (right).
Wavelength conversion
Optical communications networks using WDM can employ wavelength-based network routing.11 Here a light path — the optical equivalent of an electronic-based circuit-switched network (similar to a telephone system) — is allocated a free wavelength. The crucial point is that the same wavelength must be maintained over the entire connection, resulting in a wavelength-continuity constraint. The role of wavelength conversion is to transfer data at the input wavelength onto an arbitrary output wavelength, thereby resolving this constraint.
We have investigated the feasibility of wavelength conversion in chalcogenide waveguides using cross-phase modulation with sideband filtering.12,13 Figure 5 shows the principle: A continuous-wave probe experiences cross-phase modulation from co-propagating signal pump pulses, which spectrally broadens the probe. A bandpass filter subsequently selects a particular wavelength of the broadened probe, and the information that was present on the signal is now present on the new wavelength; i.e., λ2 + Δ in Figure 5.
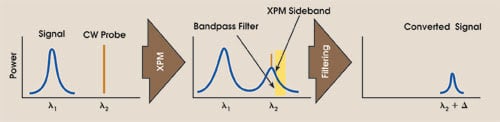
Figure 5. Shown is the principle of cross-phase-modulation wavelength conversion. An amplified pulsed pump signal (at λ1) imposes a nonlinear frequency chirp onto a copropagating wavelength-tunable CW probe (at λ2) through the nonlinear refractive index. Filtering one of the cross-phase-modulation-generated sidebands results in wavelength conversion to λ2 + Δ.
In our experiments, we used 2-ps pump pulses from a 10-GHz fiber laser modulated with pseudorandom data and combined with a CW probe from a tunable laser diode. The combined optical field was injected directly into the waveguide by butt-coupling the fiber directly to the facet. The output of the As2S3 waveguide was then sent through a 1-nm filter offset to longer wavelengths to remove the pump and select a single cross-phase modulation sideband.
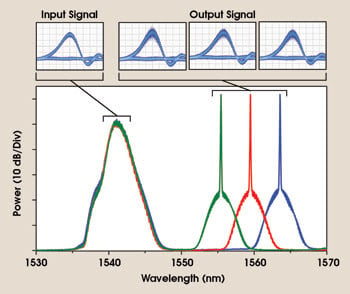
Figure 6. These spectra from the waveguide output show the input signal and three CW probes with cross-phase-modulation sidebands imprinted on them. High-speed photodiode traces above (5 ps per division) for the input and converted output signals (after sideband filtering) show good conversion.
Figure 6 shows the optical spectrum before and after the waveguide, showing the spectral broadening of the CW probe. The bit error ratio of the converted pulses showed that the signal quality (Q-factor) was degraded by only 2.3 dB compared with that of the input signal. Using this scheme, we have demonstrated error-free wavelength conversion over a 25-nm range.12 Calculations show that the device should be able to perform conversion over at least 50 nm, allowing the entire optical communications band to be covered.
Optical signal regeneration
An interesting application of chalcogenide waveguides is signal regeneration. Regeneration is necessary because of the signal degradation caused by losses, dispersion, noise, crosstalk and nonlinear processes. Several regeneration architectures that rely on optical nonlinear effects have been proposed to replace the optoelectronic regenerators currently used in long-haul systems. A particularly elegant design is based on self-phase modulation. The intensity-dependent refractive index causes an intensity-dependent phase delay that spectrally broadens the pulse. Figure 7 shows how this maps the amplitude of the optical signal onto the wavelength. A filter then selectively passes the intense “ones” while blocking the weak noise in the “zeros,” which undergoes negligible spectral broadening. This results in a steplike power transfer function that reduces noise in both “zeros” and “ones.”
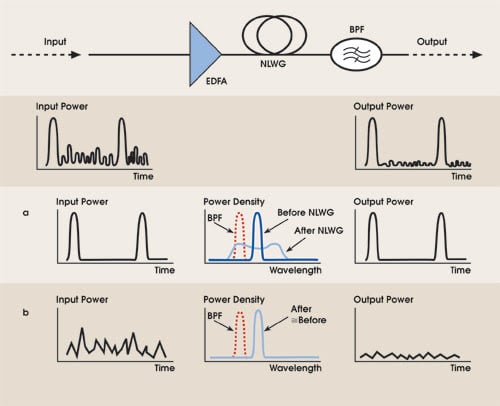
Figure 7. The principle of an optical regenerator based on self-phase-modulation broadening and filtering within a nonlinear waveguide (NLWG) is shown. (a) A signal with high peak power experiences strong self-phase-modulation-induced spectral broadening and so passes through the offset bandpass filter (BPF). (b) Amplified spontaneous emission noise experienceslittle broadening and is consequently blocked by the BPF. EDFA = erbium-doped fiber amplifier.
This scheme inherently results in a frequency offset of the output signal with respect to the input signal. For applications where this is undesirable, two regenerators can be cascaded, resulting in transparent operation. Such a scheme, combined with a retiming stage, has been used to transmit data at 40 Gb/s over 1 million kilometers using a recirculation system configuration.14
We explored these functions first by using a chalcogenide glass fiber15 to assess performance, and then we moved on to a more ambitious planar waveguide approach.16 The single-mode chalcogenide glass fiber was based on As2S3, which has a nonlinearity of 400 times that of silica; however, the area of the core is relatively large, resulting in lower optical intensities. For this demonstration, we employed a 2.8-m-long As2S3 single-mode fiber that combined with 5.8-ps transform-limited pulses from a mode-locked laser near 1550 nm. The output of the fiber was passed through a tunable 0.56-nm bandpass filter, offset by 1.3 nm from the input center frequency.
The data points in Figure 8 correspond to the measured nonlinear power transfer function. Output power limiting function at ~8-W peak input power, as well as threshold behavior, is clearly evident. The former is effective in suppressing the noise in the logical ones, while the latter contributes to suppressing noise in the zeros.
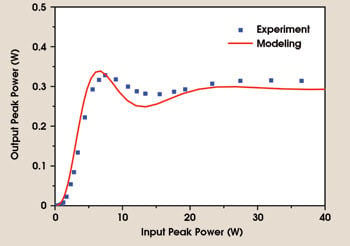
Figure 8. The power transfer function for the As2Se3 chalcogenide glass-based optical regenerator is very nonlinear. The model illustrated here is based on solving numerically the propagation of optical pulses in nonlinear dispersive waveguides.
To further reduce the device size, we have examined a photonic integrated chip-based regenerator design. Here we used a low-loss 5-cm-long As2S3 rib waveguide. Figure 9a shows the pulse spectra versus power for a bare waveguide produced using ~50 W of peak power. Two Bragg gratings were inscribed successively at the end of the waveguide using interferometric techniques similar to those used in writing silica fiber Bragg gratings.8 The two Bragg gratings, shown in Figure 9b, formed a bandpass filter for the self-phase-modulation regeneration scheme. Figure 9c shows the resulting power transfer function.

Figure 9. The spectrum of a pulse broadens (bottom to top) because of self-phase modulation as it propagates through a waveguide (a). A bandpass filter consisting of two sequential offset Bragg gratings blocks most of the unbroadened pulse but transmits a significant portion of the broadened pulse (b). The resulting power transfer curve is nonlinear and is the basis for an integrated signal regenerator (c).
Future prospects
All-optical signal processing commensurate with next-generation data formats (e.g., 160 to 640 Gb/s) requires significant improvements in the device performance. The key issue is to lower the operating power because, at present, our chalcogenide waveguide devices have required peak powers of several watts. Fortunately, there is a clear path to a reduction of a factor of ~30 to 50, and a more speculative path to a further factor of 5 or 10. These involve an increase in device length, more nonlinear glasses and a reduction in mode area.
Chalcogenide glass research is pushing ahead on several frontiers. Other areas that we feel chalcogenide glasses offer interesting prospects include Bragg solitons, directional couplers and photonic crystal cavities. The mid-infrared transparency of these materials is also of significant interest, and we expect an increasing number of sensing devices for applications in molecular fingerprint analysis and astronomy.
Meet the authors
Benjamin J. Eggleton is an ARC Federation fellow and professor of physics at the University of Sydney. He is research director of the Centre for Ultrahigh-bandwidth Devices for Optical Systems (CUDOS); e-mail: [email protected] .
Vahid G. Ta’eed is a research associate with CUDOS; e-mail: [email protected].
Barry Luther-Davies is an ARC Federation fellow and professor of physics at Australian National University. He is head of the Laser Physics Centre and a chief investigator for CUDOS; e-mail:[email protected] .
References
1. J.A. Savage (January 1982). Optical properties of chalcogenide glasses. JOURNAL OF NON-CRYSTALLINE SOLIDS, pp. 101-115.
2. A.B. Seddon (May 1995). Chalcogenide glasses: A review of their preparation, properties and applications. JOURNAL OF NON-CRYSTALLINE SOLIDS, pp. 44-50.
3. T.M. Monro and H. Ebendorff-Heidepriem (August 2006). Progress in microstructured optical fibers. ANNUAL REVIEW OF MATERIALS RESEARCH, pp. 467-495.
4. E.M. Vogel, M.J. Weber and D. M. Krol (December 1991). Nonlinear optical phenomena in glass. PHYSICS AND CHEMISTRY OF GLASSES, pp. 231-254.
5. R.E. Slusher et al (June 2004). Large Raman gain and nonlinear phase shifts in high-purity As2Se3 chalcogenide fibers. JOURNAL OF THE OPTICAL SOCIETY OF AMERICA B-OPTICAL PHYSICS, pp. 1146-1155.
6. G.I. Stegeman and E.M. Wright (March 1990). All-optical waveguide switching. OPTICAL AND QUANTUM ELECTRONICS, pp. 95-122.
7. T.K. Liang and H.K. Tsang (September/October 2004). Nonlinear absorption and Raman scattering in silicon-on-insulator optical waveguides. IEEE JOURNAL OF SELECTED TOPICS IN QUANTUM ELECTRONICS, pp. 1149-1153.
8. M. Shokooh-Saremi et al (July 2006). High-performance Bragg gratings in chalcogenide rib waveguides written with a modified Sagnac interferometer. JOURNAL OF THE OPTICAL SOCIETY OF AMERICA B-OPTICAL PHYSICS, pp. 1323-1331.
9. J.S. Sanghera et al (September 2001). Applications of chalcogenide glass optical fibers at NRL. JOURNAL OF OPTOELECTRONICS AND ADVANCED MATERIALS, pp. 627-640.
10. Y.L. Ruan et al (Oct. 18, 2004). Fabrication and characterization of low loss rib chalcogenide waveguides made by dry etching. OPTICS EXPRESS, pp. 5140-5145.
11. B. Ramamurthy and B. Mukherjee (September 1998). Wavelength conversion in WDM networking. IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, pp. 1061-1073.
12. V.G. Ta’eed et al (Oct. 30, 2006). Error free all optical wavelength conversion in highly nonlinear As-Se chalcogenide glass fiber. OPTICS EXPRESS, pp. 10371-10376.
13. V.G. Ta’eed et al (Nov. 13, 2006). All optical wavelength conversion via cross phase modulation in chalcogenide glass rib waveguides. OPTICS EXPRESS, pp. 11242-11247.
14. G. Raybon et al (2002). 40 Gbit/s pseudo-linear transmission over one million kilometers. Technical Digest of Optical Fiber Communication Conference and Exhibit, OFC 2002, Anaheim, Calif., pp. FD10-1-FD10-3.
15. L.B. Fu et al (Sept. 19, 2005). Investigation of self-phase modulation based optical regeneration in single mode As2Se3 chalcogenide glass fiber. OPTICS EXPRESS, pp. 7637-7644.
16. V.G. Ta’eed et al (May/June 2006). Self-phase modulation-based integrated optical regeneration in chalcogenide waveguides. IEEE JOURNAL OF SELECTED TOPICS IN QUANTUM ELECTRONICS, pp. 360-370.