The control of spontaneous emission opens opportunities in the development of efficient miniature lasers for displays and telecom, in quantum computing and in many other fields.
Dr. Peter Lodahl and Dr. Willem L. Vos, University of Twente
Nearly two decades ago, photonic bandgap crystals were proposed as the ultimate means for controlling the propagation and emission of light.1,2 Since that time, research into photonic crystals has exploded, with much attention devoted to controlling propagation.3 In contrast, an experimental demonstration of their use to control the emission of light has so far been absent.
We recently demonstrated experimentally that both the direction and the time of spontaneous emission can be controlled,4 thereby confirming the original proposal by Eli Yablonovitch1 that founded the field of photonic crystals. We believe that this work opens opportunities for the development of solid-state quantum optics using photonic crystals, in addition to possible applications for efficient micro LEDs, lasers or even solar cells.
Photonic bandgaps
Photonic crystals are composite dielectric structures that feature a periodic variation in their refractive index on the order of the wavelength of light. In a photonic crystal, light of specific wavelengths is prohibited from propagating in certain directions. This effect is the same as the Bragg diffraction of x-rays in solid-state crystals.
At optical frequencies, however, much larger variations of the refractive index are feasible. The larger the difference in the refractive indices between the two materials of the photonic crystal, the greater the effect on the light’s behavior. In the most extreme situation, light is prohibited from propagating in any direction — in which case a photonic bandgap is said to exist.
Such photonic bandgaps have intriguing consequences; for example, an excited light emitter — such as an atom, a molecule or a quantum dot — that is placed inside the structure will not be able to emit light. Hence, photonic crystals provide a way of inhibiting the spontaneous emission of light.
The effect of a photonic bandgap is quantified in terms of the so-called local density of states that describes the number of available electromagnetic modes in which photons may be emitted at the location of the emitter. The local density of states can be interpreted as the density of vacuum fluctuations and is determined by the structure of the dielectric material surrounding the emitter.
In the so-called Wigner-Weisskopf approximation, the radiative decay rate γR of an excited emitter is related to the local density of states ρ through Fermi’s golden rule:
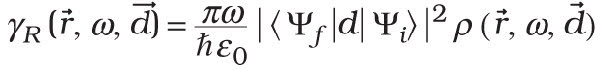
From this equation, we see that control over the local density of states provides a way of modifying spontaneous emission of light. A schematic representation of the local density of states in a photonic bandgap crystal and in a homogeneous medium is given in Figure 1. In a homogeneous medium, the local density of states is obviously independent of position and varies quadratically with frequency. In a bandgap, however, the local density of states is strongly reduced and, ideally, vanishes.
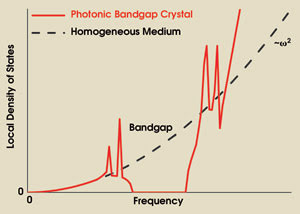
Figure 1. A schematic representation of the local density of states as a function of frequency for a homogeneous medium and a photonic bandgap crystal illustrates that it increases quadratically with frequency in a homogeneous medium but vanishes in a bandgap. For certain frequencies outside the bandgap, the local density of states can be strongly enhanced.
For certain frequencies outside the bandgap, the local density of states will be enhanced because the frequency-integrated number of states relative to the number of states in a homogeneous medium is a conserved quantity.6 A reduced local density of states means that spontaneous emission will be delayed, while an enhanced local density of states speeds up the emission process. Consequently, photonic crystals offer a way of inhibiting and enhancing emission, obtaining complete control over spontaneous emission of light.
Wide frequency bandwidth
The potential to change the radiative decay rate by altering the dielectric properties of the surroundings of the emitter also is referred to as the Purcell effect, and is well-known for light sources in high-quality cavities. A unique advantage of photonic crystals, compared with cavities, is the extremely wide frequency bandwidth within which spontaneous emission can be controlled. (Here we are referring to the enhancement of spontaneous emission that takes place in a cavity, which is a different effect from stimulated emission.)
An important parameter to consider in a real experiment on the control of spontaneous emission by photonic crystals is the efficiency of the light source. Solid-state light sources, such as the quantum dots considered here, are not ideal two-level systems because of either external influences or complex internal structures. Therefore, decay processes other than the radiative process that the photonic crystal is designed to control may contribute to the total decay rate.
The influence of unwanted processes is quantified in terms of the quantum efficiency of the light source, which is defined as the radiative decay rate relative to the total decay rate; i.e., the sum of the radiative and all nonradiative decay rates of the excited state. A high quantum efficiency of the emitter used in an experiment is crucial to control the lifetime of spontaneous emission.
The experiments were performed on extended, strongly interacting, three-dimensional photonic crystals consisting of a face-centered-cubic structure of air spheres in a titania backbone material (Figure 2).7 The refractive index contrast between titania and air is 2.7.

Figure 2. A scanning electron microscope image of a photonic crystal (left) reveals air spheres (black holes) in a titania structure (white material). The airholes are ordered in a face-centered cubic crystal structure. In the optical microscope image (right), a titania inverse opal with a lattice parameter of 370 nm displays blue opalescence, the result of optical Bragg diffraction of light.
Our group has developed a versatile three-step process to fabricate inverse opals. First, an artificial opal is constructed by self-assembly of polystyrene spheres. Such a template is already a photonic crystal, but with a small refractive index contrast. To increase the contrast, the polystyrene opal is infiltrated with titania, and the polystyrene is subsequently etched away to obtain the favorable inverted structure.7
The typical dimensions of the crystals are approximately 1 mm3, and they feature thousands of airholes in each direction. The separation between the airholes is specified in terms of the lattice parameter that measures the distance between (111) lattice planes of the crystal structure. For the experiments, we fabricated many photonic crystals with lattice parameters ranging from 240 to 650 nm.
We used colloidal quantum dots made from the semiconductor material CdSe as internal light sources.8 Quantum dots are highly efficient emitters with discrete and narrow emission lines, and therefore often are referred to as “artificial atoms.” Their advantage is that their optical properties can be tailored: The emission frequency may be tuned by varying the size of the quantum dot. The dots emit light as a result of the recombination of an electron-hole pair (exciton), and the size-dependent emission is a direct consequence of quantum-confinement of the exciton due to the nanometer-scale size of the particles. These properties make quantum dots the ideal choice for light sources in photonic structures, both in the visible region and in near-IR telecom bands.
We fabricated the quantum dots by chemical synthesis and dissolved them in a solution of chloroform and butanol.4 Our photonic crystals were infiltrated with the solution of quantum dots, then dried, creating a distribution of quantum dots on the titania surfaces inside the inverse opal. The ensemble of quantum dots had an average diameter of 4.5 nm, with a size dispersion of 5 percent. The quantum efficiency of the solution was >50 percent.
We excited the quantum dots in the photonic crystals with a picosecond optical pulse at a wavelength of 440 nm. The spontaneously emitted photons were spectrally resolved and recorded with a photomultiplier. Both the angular distribution and the decay in time of the emission were recorded. The latter experiment utilized a time-correlated single-photon-counting technique to measure the arrival time of the emitted photons with a resolution of better than 100 ps.
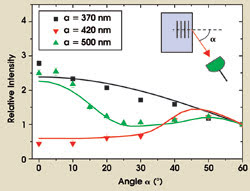
Figure 3. The graph depicts the measured intensity of spontaneous emission from quantum dots in three titania inverse opals with different lattice parameters (a) as a function of the detection angle (α) and at a fixed wavelength (630 nm). The intensities were divided by the measurement performed at 60°, a suitable reference because no stopbands appeared at this angle for all three samples.
The continuously emitted light intensity is expected to be strongly angular-dependent because of optical Bragg diffraction-forming stopgaps along certain propagation directions. Figure 3 displays the measured angular distribution on three selected photonic crystal samples with different lattice parameters. We measured the intensity at a fixed optical frequency as a function of the detection angle, defined relative to the normal of the (111) lattice planes. The sample with a lattice parameter of 370 nm was effectively a reference sample because the lattice parameter was so short that variations in the local density of states and optical stopgaps were at much shorter wavelengths than the emission range of the quantum dots.
The advantage of our reference sample is that it was prepared in the same way as the photonic crystals and therefore provides a reliable, chemically identical reference. On the sample, the intensity decreased monotonously with angle, which turns out to be a peculiar effect of ubiquitous disorder present in all real photonic crystals that cause light to be diffuse yet directional.9
On the photonic samples with lattice parameters of 420 and 500 nm, we noted strong suppression of light along certain directions, which is a direct observation of Bragg diffraction on the spontaneously emitted light. Using our newly developed theoretical model for the propagation of light in photonic crystals,9 we obtained excellent agreement between experiment and theory (see curves in Figure 3).10 Hence, a complete understanding of the propagation of light was accomplished, a prerequisite before carrying out more involved time-resolved experiments.
Furthermore, the angular measurements proved that the detected emission was dominated by light from quantum dots embedded deeply inside the three-dimensional photonic crystal that should be susceptible to the modified local density of states. Finally, the angle-resolved results may have practical applications in directional emission of solid-state light sources.10
In the time-resolved experiments, we measured the decay rate of the excited state of the quantum dots in the photonic crystals. A representative selection of our experimental data is shown in Figure 4 for three crystals with varying lattice parameters. Two emission sources contributed to the decay curves: For short times (<5 ns), a substantial contribution to the emission stemmed from luminescence from the titania backbone of which the photonic crystals consist. Beyond 5 ns, this contribution was negligible, and we detected emission only from the quantum dots.
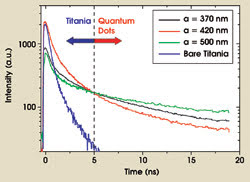
Figure 4. In this plot of the time-resolved emission from quantum dots in photonic crystals with different lattice parameters (a), the first part of the decay curves is influenced by emission from titania. After 5 ns, the emission is dominated by the quantum dots. The decay rate of the quantum dots is observed to depend on the lattice parameter.
From the data in Figure 4, we see that the decay time depends strongly on the lattice parameter of the photonic crystal. For a lattice parameter of 420 nm, we measured a faster decay, and for 500 nm, a slower decay relative to the reference sample, which had a lattice parameter of 370 nm. By modeling the decay curves, we deduced that the spontaneous emission lifetimes (the inverse of the decay rate) were 9.6 and 19.3 ns for the samples with lattice parameters of 420 and 500 nm, respectively. On the reference sample, a lifetime of 12.4 ns was obtained.
Our results demonstrate that the spontaneous emission lifetime can be both extended and shortened with a photonic crystal. These measurements represent the first direct experimental verification of the 17-year-old prediction by Yablonovitch.
The results of a detailed analysis of the decay rate as a function of emission frequency on four photonic crystals are plotted in Figure 5. The black circles are the measurements on the reference sample, and these data agree well with a calculation of the decay rate using Fermi’s golden rule and the local density of states for a homogeneous medium (orange curve, scales as ω3).
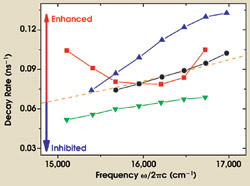
Figure 5. The measured decay rate is plotted against emission frequency for four samples with lattice parameters of 370 nm (black circles), 420 nm (red squares), 500 nm (green inverted triangles) and 580 nm (blue triangles). The curves between the points are guides to the eye. The dashed curve is theory for a dipole in a homogeneous medium.
For the photonic samples, we observed variations in the total decay rate of up to a factor of three by tuning frequency and lattice parameter. In contrast, the measured decay rate was independent of observation direction, which is expected from theory, since the local density of states is angle-independent. Both broadband inhibition (lattice parameter of 500 nm) and enhancement (580 nm) were observed relative to the reference sample. These measurements demonstrate that we can control spontaneous emission by varying the lattice parameter of the crystal.
Applications
Although our measurements provide the first demonstration that photonic crystals can control the radiative decay rate, other measurements on photonic crystals with low-efficiency light sources have confirmed that the local density of states is strongly modified.11 For light emitters with low quantum efficiencies, modifications in the local density of states are manifested in the total power emitted, and it is exhilarating that this effect was confirmed recently in experiments on quantum wells.12
Using such techniques, broadband inhibition of spontaneous emission was demonstrated11 for frequencies and lattice parameters consistent with our measurements. However, low-efficiency light sources do not allow time-resolved control of spontaneous emission, as has been demonstrated here.
The spontaneous emission of light can be controlled using other methods, such as a high-finesse (micro-) cavity, where spontaneous emission is enhanced for frequencies within the narrow linewidth of the cavity resonance. In that case, the emitter must be positioned near a maximum of the standing wave of the electromagnetic field so as to couple well to the cavity mode.
In a photonic crystal, in contrast, the Purcell effect is obtained without any cavity resonance and is an inherent multimode phenomenon related to the coupling of the quantum dot to many Bloch modes. Hence, spontaneous emission can be controlled with photonic crystals in a much wider spectral bandwidth than is possible with cavities. Indeed, our measurements demonstrate more than two orders of magnitude larger bandwidth than those involving state-of-the-art optical cavities.
Furthermore, no sensitive spatial control of the emitters is needed in the photonic crystal because the experiment was performed on an ensemble of quantum dots distributed over the volume of the photonic crystal. Clearly, the observation of the Purcell effect in a photonic crystal demands less-sensitive spatial and spectral control over the emitters than with a cavity. Consequently, our experiments could be carried out at room temperature, which is a major advantage from an experimental point of view. These benefits emphasize the superior performance of photonic crystals for wide-bandwidth and large-volume applications, even at room temperature.
The enhancement of spontaneous emission may have important applications for efficient light sources such as LEDs because the quantum efficiency of the source effectively is enhanced. Furthermore, enhanced emission may be utilized for generating single-photon sources of high quality — i.e., with little jitter in the emission time of the photon — for quantum information processing.
Conversely, the inhibition of emission is very useful for increasing the efficiency of photonic devices such as lasers and solar cells.1 These devices ultimately are limited by the loss of energy caused by spontaneous emission, and photonic crystals provide a way to suppress this loss. Photonic crystals also may provide a valuable tool for shielding fragile quantum information against decoherence, because the principle demonstrated here relies on the control of vacuum fluctuations.
Acknowledgments
We gratefully acknowledge Floris van Driel and Daniël Vanmaekelbergh of the University of Utrecht in the Netherlands, as well as Ivan Nikolaev, Arie Irman and Karin Overgaag for their contributions to the work presented here. We are grateful to Femius Koenderink and Ad Lagendijk for useful discussions.
References
1. E. Yablonovitch (May 18, 1987). Inhibited spontaneous emission in solid-state physics and electronics. PHYS. REV. LETT., pp. 2059-2062.
2. S. John (June 8, 1987). Strong localization of photons in certain disordered dielectric superlattices. PHYS. REV. LETT., pp. 2486-2489.
3. J.D. Joannopoulos et al (March 13, 1997). Photonic crystals: putting a new twist on light. NATURE, pp. 143-149.
4. P. Lodahl et al (Aug. 5, 2004). Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. NATURE, pp. 654-657.
5. P. Lambropoulos et al (April 2000). Fundamental quantum optics in structured reservoirs. REP. PROG. PHYS., pp. 455-503.
6. S.M. Barnett and R. Loudon (Sept. 16, 1996). Sum rule for modified spontaneous emission rates. PHYS. REV. LETT., pp. 2444-2446.
7. J.E.G.J. Wijnhoven and W.L. Vos (Aug. 7, 1998). Preparation of photonic crystals made of air spheres in titania. SCIENCE pp. 802-804.
8. B.O. Dabbousi et al (June 26, 1997). (CdSe)ZnS core-shell quantum dots: synthesis and characterization of a size series of highly luminescent nanocrystallites. J. PHYS. CHEM. B, pp. 9463-9475.
9. A.F. Koenderink and W.L. Vos (Nov. 21, 2003). Light exiting from real photonic band gap crystals is diffuse and strongly directional. PHYS. REV. LETT., 91:213902.
10. I.S. Nikolaev et al (Oct. 29, 2004). Quantitative analysis of directional spontaneous emission spectra from light sources in photonic crystals. http://arxiv.org/abs/physics/0410056.
11. A.F. Koenderink et al (March 20, 2002). Broadband fivefold reduction of vacuum fluctuations probed by dyes in photonic crystals. PHYS. REV. LETT., 88:143903.
12. S. Ogawa et al (July 9, 2004). Control of light emission by 3D photonic crystals. SCIENCE, pp. 227-229.
Meet the authors
Peter Lodahl (e-mail: [email protected]) and Willem L. Vos (e-mail: [email protected]) are members of the Complex Photonic Systems research group, part of the department of science and technology and Mesa+ research institute at the University of Twente in Enschede, the Netherlands. Lodahl is a postdoctoral fellow and, as of April, will be an associate professor at the COM research center at the Technical University of Denmark in Lyngby. Vos is a professor at the University of Twente.