Ti:sapphire laser systems are enabling a new generation of quantum computers, quantum sensors, and atomic clocks.
JOSEPH THOM, NILS HEMPLER, AND GRAEME MALCOLM, M SQUARED
A second quantum revolution is underway. The first revolution relied on an understanding of the wave-particle duality of electrons and photons, and led to the information age of smartphones, the internet, and supercomputers. Inventions of the second quantum revolution, known as Quantum 2.0, go beyond wave-particle duality to exploit the quantum-mechanical effects of superposition and entanglement. Examples include early prototype quantum computers for performing previously intractable calculations, quantum sensors that measure physical quantities with unprecedented sensitivity, and a new generation of ultraprecise atomic clocks.
Technologies that rely on finely tuned interactions between laser light and a single atom form a significant subset of the offerings of Quantum 2.0. Two internal levels of an atom, |e
and |g with frequency separation E =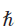 
ωatom, are chosen that can be coupled with laser radiation at frequency ωlaser (Figure 1a). In the quantum regime, the coupling between the atom and the laser is coherent, meaning that the atom’s quantum state evolves with a well-defined phase relationship with the driving laser field. This allows quantum engineers to create arbitrary superposition states of the two levels, thereby controlling the probability of finding the atom in the excited state Pe by applying laser pulses of a certain frequency, power, and duration (Figure 1b). Such coherent control methods are also used to create entangled states of multiple two-level systems.
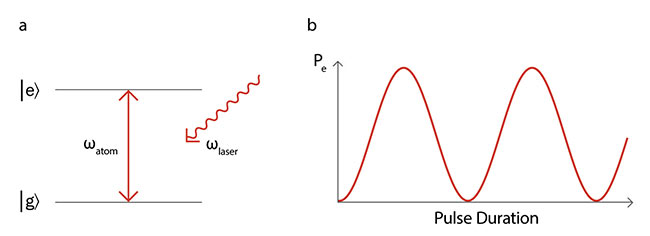
Figure 1. The concept of coherent atom-laser interactions. A two-level system with states |e and |g,
with frequency splitting ωatom, is driven by laser radiation at frequency ωlaser (a). The probability of finding
the atom in the excited state Pe evolves coherently with the duration of the laser pulse (b). Courtesy of M Squared.
How well this coherent coupling can be controlled is a fundamental limiting factor in the performance and scalability of quantum computers. It further limits the precision and stability of quantum sensors and clocks. Thus, the controllability and quality of laser light is essential to the advancement of quantum systems, and state-of-the-art laser sources are helping to make the promises of Quantum 2.0 a reality.
Quantum computing
In the context of quantum computing, a two-level system is known as a qubit. Analogous to the bit (0 and 1), the qubit is the basic unit of information in quantum computing, which derives its performance advantage from the ability of qubits to exist in coherent superpositions of both 0 and 11.
Architectures that employ lasers to manipulate qubits encoded in the internal states of single ions or atoms are leading the race to build a universal quantum computer, and they compare favorably in many aspects with the solid-state systems being developed by Google and IBM. For these laser-driven atomic qubits, quantum logic gates are created through precisely tuned laser pulses that perform the coherent control. A quantum algorithm consists of a sequence of gates, where each acts on one or more qubits.
The fidelity of each logic gate, broadly defined as the probability of reaching a target quantum state, is limited by how well the parameters of each laser pulse can be controlled. The fidelity must remain above a certain threshold to prevent a calculation from becoming infeasible due to gate errors. It follows that very high-purity and low-noise optical sources are necessary for quantum computing with ions and atoms.
Qubits based on single trapped atoms come in two varieties, defined as optical or hyperfine. With optical qubits, the levels are chosen such that the upper level is extremely long-lived, with a lifetime on the order of 1 s, resulting in a transition linewidth of ~1 Hz. This lifetime sets an upper limit to the coherence time of the atom-
laser interaction that, if maximized, allows completion of the required number of logic gates before the system loses coherence. This requires laser sources with extremely narrow emission linewidths of about 1 Hz to perform coherent control with optical qubits. Typically, out-of-the-box laser linewidths range from ~100 kHz to several megahertz, depending on the laser technology. Therefore, significant linewidth reduction is required through stabilization to high-finesse, low-drift, and vibration-insensitive optical reference cavities. Using this approach, single- and two-qubit entangling gates have been demonstrated with fidelities >99.9% with 40Ca+ ions using a Ti:sapphire laser operating at
729 nm with a 1-Hz linewidth (Figure 2).
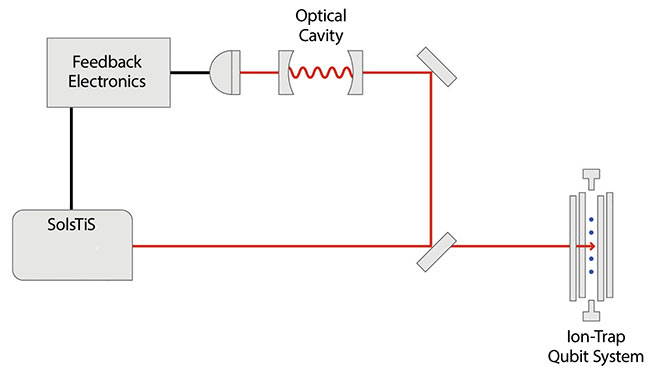
Figure 2. Stabilizing a SolsTiS Ti:sapphire laser to a high-finesse optical cavity results in a 1-Hz laser
linewidth as required for high-fidelity gate operations with optical qubits. Courtesy of M Squared.
While trapped ion systems have demonstrated some of the highest-recorded gate fidelities, the next challenge involves scaling the qubit count to the level required to realize a quantum computer that outperforms a classical device. The difficulty of this challenge derives from scaling the physical resources required to trap and control a large number of ions.
The emerging field of neutral atom quantum computing offers a promising solution to the scalability issue2. With this
approach, qubits are trapped in an ordered array of trapping sites formed by laser light. Scaling to a large number of qubits becomes a challenge in providing sufficient laser power to form the trapping potentials. Whereas the Coulomb force between neighboring qubits mediates entangling gates between trapped ions, no such interaction exists between neutral atoms. Therefore, these systems use the Rydberg blockade mechanism, which relies on long-range dipole forces of highly excited atomic states to mediate entangling gates. Multiple laser frequencies are necessary to produce these highly excited states, and each is subject to the same constraints of spectral purity as required by ion-based optical qubits.
Hyperfine qubits are encoded in two sublevels of the ground state of an alkaline-earth atom. In this case, two optical frequencies — offset in frequency by the microwave energy splitting of the qubit (typically a few gigahertz) — permit coherent coupling through stimulated Raman transitions. The two laser frequencies are generated either through sideband generation using electro-optic modulation, or by phase locking two lasers to maintain a precise frequency offset. With Raman transitions, it is not the linewidth of each frequency that dictates the quality of the coherent control but the relative phase noise between them. Also, stimulated Raman transitions are implemented nonresonantly, meaning high optical powers are necessary to achieve a sufficiently strong atom-laser coupling for high-fidelity logic gates. A laser system suitable for high-fidelity gate operations must therefore combine low phase noise with high optical power, which for hyperfine qubits is required at ultraviolet wavelengths.
Figure 3 illustrates such a laser system. For the 43Ca+ ion hyperfine qubit, two phase-locked and frequency-doubled Ti:sapphire lasers deliver >3 W total power at two frequencies offset by 3.2 GHz at 397 nm. With an integrated phase noise of 7 mrad rms from 10 kHz to 1 MHz, the system is designed for very high-fidelity quantum logic gates.
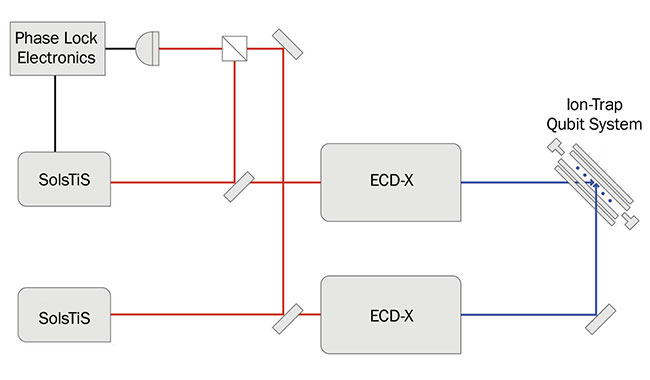
Figure 3. Frequency-doubled and phase-locked systems that employ Ti:sapphire lasers have generated
high-fidelity entangling gates with hyperfine ion-trap qubits. ECD-X: external cavity doubler. Courtesy of M Squared.
Research has demonstrated single- and two-qubit fidelities suitable for fault-
tolerant processing with small numbers of qubits in ion and neutral atom systems. But many challenges remain before the performance benefits of large-scale quantum computing become possible. For example, laser systems that can accommodate the thousands of physical qubits required for universal quantum computation will require greatly increased output power while maintaining the low noise levels required for the highest-fidelity gates. Innovations in integrated optics and optical modulator technology will also help enable distribution of laser light across such a large qubit array. Such developments will be critical before a system using laser-driven qubits can deliver the performance advantage of quantum computers.
Quantum sensors
While a universal quantum computer is still years away, quantum sensors are much closer to commercial reality. Quantum sensors based on atom interferometry, for example, are already helping to measure tiny variations in acceleration due to gravity from hidden underground objects and voids. Quantum gravimeters can also monitor natural phenomena such as Earth tides and volcanic activity.
Atom interferometers that combine acceleration and rotation measurements are also emerging for quantum inertial navigation systems, in which long-term accuracy is guaranteed by an absolute atomic reference. This offers alternatives to current inertial systems, which suffer from measurement bias drifts that make long-term navigation highly inaccurate, as well as to satellite navigation systems, which do not work in submarine and subterranean environments and are subject to jamming and spoofing.
An atom interferometer measurement sequence starts by preparing a cold atom cloud of about 5 µK through laser cooling in a magneto-optical trap (Figure 4a). After the trap is turned off, the atoms are in free fall and interact with three laser pulses from a pair of vertically counter-propagating beams. In analogy with the optical Mach-Zehnder interferometer, the pulses form the beamsplitters and combiners for the atomic wave functions (Figure 4b). These matter-wave optics are implemented with stimulated Raman transitions, as employed in quantum computing systems using hyperfine qubits. The
counter-propagating laser beams serve as an optical ruler that measures the position of the atoms as they fall, and the precision of the optical ruler is limited by the relative phase noise of the two frequencies. So, exceptionally low-phase-noise laser systems are critical for acceleration and rotation measurements of the highest sensitivity.
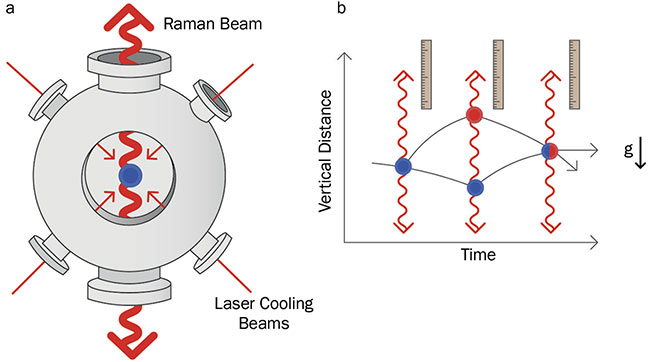
Figure 4. Measurements of acceleration with an atom interferometer. Atoms are prepared in a magneto-optical trap through laser cooling and then allowed to free-fall relative to a reference Raman beam (a). Three counter-propagating pulses act as an optical ruler for the free-falling atoms (b). Courtesy of M Squared.
In addition to providing an optical ruler for acceleration measurements, atom interferometers require laser light at multiple optical frequencies for laser cooling, quantum state preparation, and detection of the atomic population at the end of the interferometer sequence. For an atom interferometer based on 87Rb, these frequencies are separated by ~1 GHz at 780 nm. The laser system must switch between these frequency configurations on a timescale that is short compared to the total measurement sequence (~100 ms). High optical powers are necessary to enable the use of large beams for the optical ruler to ensure that the free-falling atoms see negligible wavefront curvature during free fall. Finally, the laser system must be compact and robust enough to operate on a transportable platform. Laser systems that combine these requirements have leveraged laser diode-based systems3, frequency-doubled fiber lasers4, and Ti:sapphire solid-state systems (Figure 5). These have already been deployed in high-sensitivity atom
interferometers on moving platforms.
Figure 5. A transportable system, composed of two Ti:sapphire lasers, that has been used to operate an atom interferometer on a moving platform. Courtesy of M Squared.
Benefitting from the high level of sensitivity and accuracy enabled by finely tuned atom-laser interactions, quantum technologies are well-positioned to offer disruptive measurement capabilities to industries that rely on high-performance sensors. Transportable and low-maintenance laser systems able to implement coherent control in harsh environments will be critical if this advantage is to be fully
exploited.
Atomic clocks
Many aspects of society, such as high-frequency financial trading, network
synchronization, and satellite navigation systems, depend on the timekeeping accuracy of atomic clocks.
Figure 6 illustrates the operational principle of an atomic clock. A high-
frequency oscillator generates radiation at a frequency close to a well-known transition frequency of a two-level system — chosen to be minimally sensitive to external perturbations, such as stray magnetic fields and blackbody radiation. By providing feedback to the oscillator frequency using a frequency shifter, exact resonance with the transition is maintained through successive interrogations of the atom. In practical terms, the tick rate of the oscillator is referenced to the atomic transition, which serves as an absolute frequency reference.
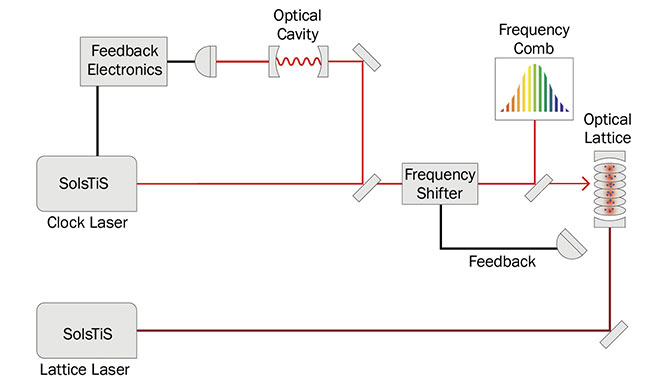
Figure 6. The operational principle of an atomic clock. A highly stable clock laser is referenced to an atomic transition through successive interrogations of the atomic sample. Courtesy of M Squared.
In the 1950s, the very first atomic clocks leveraged interrogation of hyperfine transitions in a beam of cesium atoms using microwave radiation. The definition of time itself is still based on such microwave clocks, and they underpin many applications, such as providing a timing reference for global navigation satellite systems. Today, development is underway for a new generation of atomic clocks that employs ultranarrow linewidth lasers to interrogate extremely narrow atomic transitions in ultracold atomic samples. This method has enabled optical atomic clocks that use single ions or arrays of neutral atoms, both of which have surpassed the performance of microwave clocks. These new clock designs require ultranarrow linewidth laser light to interrogate the atomic sample and provide the ticks of the clock. Because it is not possible to count the oscillations of this laser directly, self-referenced frequency combs convert the tick rate from the optical to the radio frequency domain, where it can be counted electronically5.
While ion clocks trap the reference atom using electric fields, neutral atom clocks use laser light to form an optical lattice that traps the atoms in an array while they are interrogated. To maximize the signal-to-noise ratio of each measurement cycle and improve clock stability, this lattice laser must output high optical powers because the number of atoms that can be trapped in the array scales with laser power.
Operating the laser that forms the lattice at a magic wavelength also improves clock accuracy by nulling the shift of the two-level system energy splitting caused by the Stark effect. A highly stable power output is also critical, because power fluctuations contribute to the shaking and subsequent heating of the atoms trapped in the lattice. This degrades the frequency stability of the clock.
An ideal lattice laser will combine high-power and exceptionally low-power noise with an output that remains fixed at the magic wavelength. Ti:sapphire lasers fulfill these requirements, and many of the leading optical clock research groups choose this platform for their optical
lattice clocks, which can now reach 5 × 10−17 fractional instability after only 1 s of averaging time6.
This unprecedented level of performance is typically found in laboratory-based systems used for applications where portability is not a requirement, or where stable timing signals can be distributed from a master clock over fiber networks. Other applications, such as geodesy and navigation, will require portable optical atomic clocks. Portability demands the
development of miniaturized lasers that can match the frequency stability and power capabilities of current state-of-the-art systems.
The successful deployment of many quantum technologies, namely those that rely on finely tuned interactions between atoms and laser light, is underpinned by laser sources that combine tunability and high power with exceptional stability and spectral purity. Ti:sapphire lasers fulfill these criteria, and are thus deployed in some of the world’s most advanced quantum computers, quantum sensors, and atomic clocks. This trend is expected to continue as the potential benefits of Quantum 2.0 are brought to fruition.
Meet the authors
Joseph Thom has been a quantum technology scientist at M Squared, a photonics and quantum technology company, since 2016. He holds a master’s degree in physics from the University of St. Andrews, and he was awarded a doctorate in engineering from the University of Strathclyde for experimental work carried out at the National Physical Laboratory; email: [email protected].
Nils Hempler is a multidisciplinary scientist with a flair for physics, engineering, innovation, and business. At M Squared, he leads the innovation division and plays a pivotal role in developing technologies for new and emerging markets, including quantum technologies; email: [email protected].
Graeme Malcolm is CEO and founder of M Squared, which is headquartered in Scotland, with offices located globally. He is deeply committed to applying technological and entrepreneurial solutions to some of society’s most significant problems, including improving health care, halting climate change, and ushering in a new generation of quantum solutions; email: [email protected].
References
1. T. Ladd et al. (2010). Quantum computers. Nature, Vol. 464, Issue 45, pp. 45-53.
2. M. Saffman (2016). Quantum computing with atomic qubits and Rydberg interactions: progress and challenges. J Phys B: At Mol Opt Phys, Vol. 49, Issue 20, p. 202001.
3. J. Fang et al. (2018). Realization of a compact one-seed laser system for atom interferometer-based gravimeters. Opt Express, Vol. 26, Issue 2, pp. 1586-1596.
4. F. Theron et al. (2014). Narrow linewidth single laser source system for onboard atom interferometry. Appl Phys B, Vol. 118, Issue 1, pp. 1-5.
5. T. Fortier and E. Baumann (2019). 20 years of developments in optical frequency comb technology and applications. Commun Phys, Vol. 2, Issue 153, pp. 1-15.
6. T. Bothwell et al. (2019). JILA SrI optical lattice clock with uncertainty of 2.0 × 10−18. Metrologia, Vol. 56, Issue 6, p. 065004.