How can the group velocity of a pulse of light propagating through a dispersive material exceed the speed of light in vacuum without violating Einstein’s special theory of relativity?
Daniel J. Gauthier, Duke University, and Robert W. Boyd, University of Rochester
The speed of light in vacuum (c ≈ 3 × 108 m/s) is an important physical constant that appears in Maxwell’s theory of electromagnetism. For this reason, scientists have endeavored to measure it with very high precision, making it one of the most accurately known of all physical constants. The situation becomes murkier for a slightly different situation: Send a pulse of light through a dispersive optical material rather than vacuum, and bizarre things start to appear. For example, under conditions such that the dispersion of the medium is anomalous over some spectral region,1 as described in greater detail below, it is possible to observe the peak of a pulse of light apparently leaving a piece of dispersive material before it enters.
Fast light
The possibility of such “fast light” behavior has been known for nearly a century and has been the source of continued controversy and confusion. Some of the controversy arises because some people interpret Einstein’s special theory of relativity as placing a speed limit of c on any sort of motion. Yet, a rather simple mathematical proof shows that fast light behavior is completely consistent with Maxwell’s equations that describe pulse propagation through a dispersive material and, hence, does not violate Einstein’s special theory of relativity, which is based on Maxwell’s equations. Although the proof is straightforward, great care must be taken in interpreting the special theory of relativity and in determining whether experimental observations are consistent with its predictions.
From our point of view, the special theory of relativity places a speed limit on the transfer of information between two parties, and all experiments performed to date are consistent with the speed limit being interpreted in this manner.
To understand the basics of fast-light pulse propagation, it is crucial to realize that there are many quantities that can be introduced to describe the speed at which a light pulse moves through a material system.2 This confusing situation arises from the fact that a pulse propagating through any material system will experience some level of distortion — e.g., it spreads out in time and reshapes — and, hence, a single velocity cannot be used to describe the motion of the pulse.
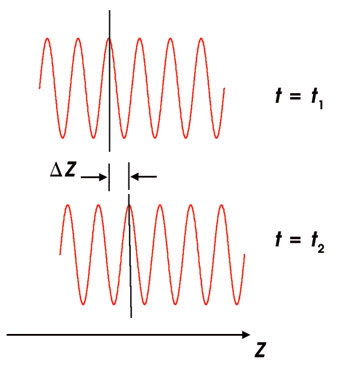
Figure 1. A monochromatic electromagnetic wave propagates through an optical material. Snapshots of the electric field distribution are shown at two different times. The phase velocity describes the speed of the crests of the wave. The distance traveled by a crest in the time interval t2–t1 is denoted by ΔZ.
Probably the most familiar such quantity is the phase velocity of light. Consider a continuous-wave monochromatic (single frequency) beam of light of frequency ωc; the electromagnetic field oscillates rapidly (the oscillation period is ~1.8 fs for green light). The phase velocity νp describes the speed at which the crests of these oscillations propagate, as shown in Figure 1. In a material system characterized by the frequency-dependent index of refractions n(ω), the phase velocity is defined as:
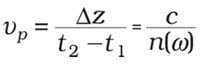The situation becomes more complicated when a pulse of light propagates through a dispersive optical medium. According to Fourier’s theorem, a pulse of duration τ is necessarily composed of a range of frequencies. In a sense, a pulse can be thought of as resulting from constructive and destructive interference among the various Fourier (frequency) components. At the peak of the pulse, these components will tend to add up in phase, while interfering destructively in the temporal wings of the pulse, as shown in Figure 2.
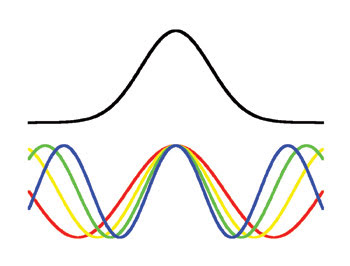
Figure 2. Sinusoidal component waves interfere to create a pulse of light.
In a material with a frequency-dependent refractive index, each frequency propagates with a different phase velocity, thereby modifying the nature of the interference. If n(ω) varies linearly with frequency ω, the effect of the modified interference is to shift the peak of the pulse in time, but with the pulse shape staying the same. The fact that the pulse is temporally shifted implies that it is traveling with a velocity different from the phase velocity. This new velocity is known as the group velocity and is defined as:
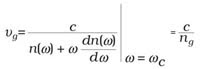where ωc is the central frequency and ng is the group index of the material. We see that ng differs from the phase index by a term that depends on the dispersion dn/dω of the refractive index. For slow light, which occurs for ng >1, the point of constructive interference occurs at a later time. For fast light, which occurs for ng <1, it occurs at an earlier time.
A crucial observation is that the physics behind fast light is identical to the physics behind slow light. Although most of us readily accept the notion of a pulse of light moving through a dispersive material at a group velocity less than c, many of us are uncomfortable with the fast light case. We shouldn’t be. Both arise from the same effect: the shifting of the point of constructive interference to another point in space-time.
Little distortion
Fast light is achieved by making dn/dω large and negative and is invariably achieved by making use of the rapid variation of refractive index that occurs in the vicinity of a material resonance. What is perhaps most significant about recent research in fast light is not the existence of the effect but rather the realization that certain pulse shapes can propagate through a highly dispersive medium with negligible pulse distortion. To prevent pulse distortion, higher-order dispersion — arising from the nonlinear dependence of n(ω) on ω — must be minimized. Recent fast-light experiments have been conducted in a regime that minimizes higher-order dispersion by ensuring that the pulse bandwidth is limited to the spectral region over which there is essentially a linear variation of n(ω). This limit implies that the pulse duration can’t be too short or have sudden changes in amplitude or phase. The key to understanding how fast light is consistent with the special theory of relativity is tied into the details of how sudden changes in the pulse shape propagate through a dispersive material.
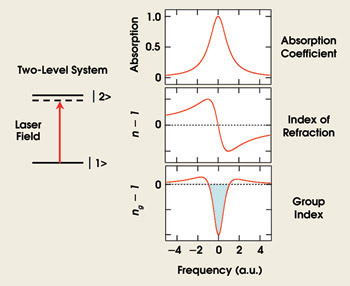
Figure 3. In a two-level system, the strong absorption resonance gives rise to a large variation in the refractive and group indices in the vicinity of the resonance. Fast light occurs whenever ng – 1 is negative. This region surrounds the exact resonance frequency and is shaded in blue in the figure.
For achieving extremely fast light propagation, it is important to find a material system for which dn/dω is as large and negative as possible. A dilute gas of atoms with a strong absorption resonance is an interesting candidate. The refractive index for such a sample is typically small (n – 1 ~ 10–3), but it varies rapidly in the region of the resonance so that dn/dω and, hence, ng can be large. This situation is shown in Figure 3. If the carrier frequency of the pulse is tuned to the resonance frequency, the anomalous dispersion becomes very large. For easily attainable conditions, νg can take on very large positive or even negative values.3,4 However, the absorption near a resonance is very high. Essentially all of the light is absorbed within a few microns, severely limiting the attainable pulse advancement.
To get around the problem of large absorption, recent fast-light research has taken advantage of anomalous dispersion between two gain lines5-7 or that due to coherent population oscillations in a reverse saturable absorber.8
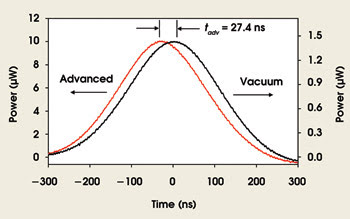
Figure 4. Experimentally observed fast-light pulse propagation is shown here. Pulse propagation through vacuum is represented by the black line, and through a gas of potassium atoms pumped by a bichromatic laser beam is shown by the red line. Adapted from Reference 7.
An example of fast-light pulse propagation is shown in Figure 4, which depicts the propagation of a smooth Gaussian pulse through vacuum in comparison with propagation through a fast-light dispersive material (a dilute gas of potassium atoms pumped by a bichromatic laser beam). The pulse propagating through the fast-light medium is amplified by a factor of seven, but it has been normalized to the same height as the vacuum-propagated pulse for easier comparison of the relative pulse advancement.
These observations compare only what happens at the output face of the medium. What occurs inside the medium is even stranger. A numerical simulation showing what happens when a pulse of light passes through a medium with a negative group index is shown in Figure 5. We see that, within the material medium, the pulse does move in the backward direction, corresponding to the negative value of the group velocity. We also see that there is a negative time delay; that is, the peak of the transmitted pulse leaves the medium before the peak of the incident pulse enters the medium.
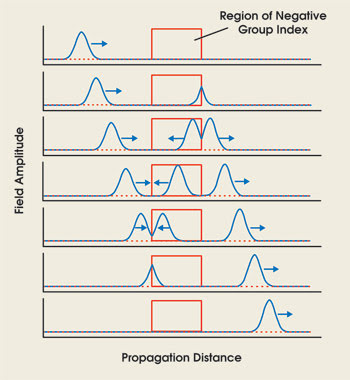
Figure 5. A time sequence of frames shows how a pulse of light propagates through a material with a negative value of the group velocity. Note that the peak of the exiting pulse leaves before the peak of the incident pulse enters, and that the pulse appears to move backward within the medium. This sort of behavior was seen in a recent laboratory experiment, although for broader pulses.
For illustration purposes, we have kept the pulse amplitude fixed; in reality, the pulse amplitude grows from left to right, as observed in a recent experiment.9 This fast-light experiment was conducted using an optical amplifier; for this reason, there is no concern with the apparent lack of energy conservation seen in the figure because energy is exchanged between the field and the medium in a transitory manner.
To understand why the behavior in Figures 4 and 5 seems so disconcerting, we need to briefly review some aspects of Einstein’s special theory of relativity. This theory concerns the behavior of Maxwell’s equations under coordinate transformations and has far-reaching consequences. In his public discussions of the theory,10 Einstein focuses on the concept of an “event,” such as a spark caused by a lightning bolt, and on how the event (or multiple events) would be observed by people at various locations. He was especially interested in observers moving with respect to a coordinate system that is stationary with respect to the events. A detailed description of his findings is not needed for this discussion, as it is necessary to consider only the properties of a single event in a single coordinate system.
Space-time plots
A convenient way to discuss the flow of information from an event is to use a space-time diagram, where the horizontal axis is a single spatial coordinate and time is plotted along the vertical axis (see Figure 6). According to the special theory of relativity, the fastest way that knowledge of an event can reach an observer is if it travels at the speed of light in vacuum. The lines that connect points in a space-time diagram that follow vacuum speed-of-light propagation define the light cone — the blue region in Figure 6a. The inverse of the slope of lines drawn in a space-time diagram is equal to the velocity.
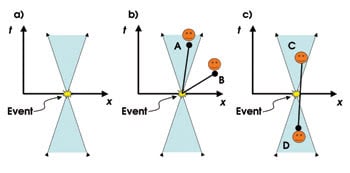
Figure 6. The lines that connect points in a space-time diagram that follow vacuum speed-of-light propagation define the light cone (a). Observers are at space-time points A and B. In a world that is relativistically causal, A observes the event, but B does not (b). If relativistic causality could be violated, a person at C could observe the event and transmit information to a person at D using a superluminal communication channel. The person at D could then change the outcome of the event (c).
Observers at space-time points within the blue cone (observer A in Figure 6b) can see the event and those outside the cone cannot (observer B in Figure 6b). The flow of information within the light cone is said to be relativistically causal. Note that the cone extending for times preceding the event represents the space-time regions where light could reach the location of the event. That is, an observer (not shown) in this region can affect the event but cannot see it.
On the other hand, the hypothetical faster-than-light propagation of information is relativistically acausal, meaning that there is no direct time-ordered link between a cause and an effect. We are not aware of any observation of acausal communication, but it is important to discuss such a hypothetical behavior because it can teach us more about our existing understanding of nature, and it clearly points out the consequences of faster-than-c information transmission.
An example of a hypothetical faster-than-light communication scheme is shown in Figure 6c, where we assume that it is possible to transmit information at a speed that is less than zero (negative velocity). If such a superluminal signal were possible, information could be transmitted from the positive-time light cone to a person at position D. This observer could change the outcome of the event (e.g., prevent it from happening) because she is located within the light cone leading to the event, but at a time before the event happens. Thus, she can change the outcome of the event. We are sure that some gamblers would pay us a lot of money if we could construct such a relativistically acausal communications system.
Fronts and precursors
One question that perplexed researchers soon after Einstein published his theory is whether pulse propagation in a dispersive medium might allow for relativistically acausal communication. By the early 1900s, it was known that some of the velocities describing pulse propagation through a dispersive material could attain values greater than c — what we now call fast light. Many eminent scientists debated whether such behavior constitutes a violation of the special theory of relativity.
Arnold Sommerfeld and his student, Léon Brillouin, took up the challenge in 1907 to see whether they could prove that information travels at subluminal speeds.11 Sommerfeld realized that the proof had to start with the definition of a “signal,” where a signal is a modulation of an electromagnetic wave that allows two parties to transmit information. In its essence, the simplest signal is one in which the wave is initially zero and suddenly turns on to a finite value — a so-called step-modulated pulse. In terms of our discussion of relativity in the preceding section, the moment that the wave turns on corresponds to the event.
In their analysis, Sommerfeld and Brillouin used Maxwell’s equations to predict the propagation of the electromagnetic wave, which was coupled to a set of equations that described how it modifies the dispersive material. For the dispersive material, they assumed that it consisted of a collection of Lorentz oscillators, simple models for an atom that describe its resonant behavior when interacting with light. Each oscillator consists of a massive (immovable) positive core and a light negative charge that experiences a restoring force obeying Hooke’s law (a simple model for the force generated by a spring). They also assumed that the negative charge experiences a velocity-dependent damping, so that any oscillations set in motion will eventually decay in the absence of an applied field.
Conceptually, an incident electromagnetic wave polarizes the material — causes a displacement of the negative charges away from their equilibrium position — acting back on the electromagnetic field to change its properties (e.g., amplitude and phase). The coupled Maxwell-Lorentz oscillator model possesses spectral regions of anomalous dispersion, where νg takes on strange values and, thus, should be able to address the controversy. The model is so good that it is still in use today for describing the linear optical response of dispersive materials.
Using fairly sophisticated mathematical methods of the time, Sommerfeld was able to predict what happens to the propagated field for times immediately following the sudden turn-on of the wave — what he called the “front” of the pulse. He showed that the velocity of the front always equals c. In other words, the front of the pulse coincides with the boundary of the light cone shown in Figure 6.
He gave an intuitive explanation for his prediction. When the electromagnetic field first starts to interact with the oscillators, the oscillators cannot immediately act back on the field via the induced polarization because they have a finite response time. Thus, for a brief moment after the front passes, the dispersive material behaves as if there is nothing there — as if it were vacuum. From the point of view of information propagation, one should be able to detect the field immediately following the front and, hence, observe information traveling precisely at c.
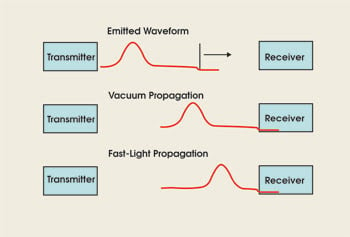
Figure 7. In a typical experiment, the emitted waveform has the shape of a well-defined pulse. Nonetheless, the waveform has a front, the moment of time when the intensity first becomes nonzero. When such a waveform passes through a fast-light medium, the peak of the pulse can move forward with respect to the front, but it can never precede the front. Thus, even though the group velocity is superluminal, no information can be transmitted faster than the front velocity, which is always equal to c.
After the front passes, mathematical predictions are very difficult to make because of the complexity of the problem. Brillouin extended Sommerfeld’s work to show that the initial step-modulated pulse, after propagating far into a medium with a broad resonance line, transforms into two wave packets (now known as optical precursors) and is followed by the bulk of the wave (what Brillouin called the “main signal”). The scientists found that the precursors tend to be very small in amplitude and, thus, it would be difficult to measure information transmitted at c; rather, it would be easier to detect at the arrival of the main signal, which they found travels slower than c. The term “precursor” is somewhat confusing because it implies that the wave packet comes before something; in this usage, the precursors come before the main signal but after the pulse front.
One aspect of Sommerfeld and Brillouin’s result that can lead to confusion is the possible situation wherein one or more of these wave packets travels faster than c. What is implied here is that a velocity can be assigned to the precursors and to the main signal to the extent that they do not distort, and that these velocities can all take on different values. In a situation where the velocity of a wavepacket exceeds c, it will eventually approach the pulse front (which travels at c), become much distorted (so that assigning it a velocity no longer makes sense) and either disappear or pile up at the front.
Still being debated
Sommerfeld and Brillouin’s research appeared to satisfy scientists in the early 1900s that “fast light” does not violate the special theory of relativity. Yet there continue to be researchers who question aspects of their work. One point of contention for some people is their belief that it is impossible to generate a waveform in the lab that has a truly discontinuous jump (i.e., there is no electromagnetic field before a particular time and then a field appears).
Yet, having something appear at a particular space-time point is precisely what is meant by an event, as described above. Thus, if one does not believe in discontinuous waveforms, then the very conceptual framework of the special theory of relativity and the associated light cone shown in Figure 6 would need to be thrown out. Many scientists are unwilling to do so. Also, the existence of optical precursors has been questioned, because Sommerfeld and Brillouin made some mathematical errors in their analysis concerning the propagated field for times well beyond the front — although recent research suggests that precursors can be observed readily in setups similar to that used in recent fast-light research.12
So how can the data shown in Figure 4 be consistent with the special theory of relativity? To answer this question, we must make a connection between Sommerfeld’s idea of a signal and the data shown in the figure. In the experiment, a pulse was generated by opening a variable-transmission shutter (an acousto-optic modulator); only a segment of the pulse is shown. At an earlier time, not shown in the figure, the light was turned from the off state to the on state, but with very low amplitude. The moment the light first turns on coincides with the pulse front (the event). At a later time, the pulse amplitude grows smoothly to the peak of the pulse and then decays.
As far as information transmission is concerned, all the information encoded on the waveform is available to be detected at the pulse front (although it might be difficult to measure in practice). The peak of the pulse shown in Figure 4 contains no new information. Thus, the fact that the peak of the pulse is advanced in time is not a violation of the special theory of relativity — so long as it never advances beyond the pulse front. Figure 8 shows a schematic of the light cone for just such a fast-light experiment.
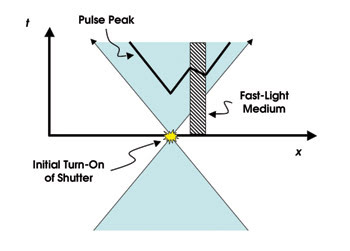
Figure 8. Pulse propagation in a fast-light medium with a negative group velocity is shown in this space-time diagram. The peak is advanced as it passes through the medium, but the pulse front is unaffected. The opening angle of the light cone is drawn differently from that in Figure 4 for illustration purposes only.
In our opinion, all experiments to date are consistent with the special theory of relativity, even though it may be difficult to show this. In some experiments, the pulse shape is such that it is exceedingly difficult to detect the pulse front and, hence, it may appear that the special theory has been violated. In other experiments especially designed to accentuate the pulse front, it has been shown that the information velocity is equal to c within the experimental uncertainties in both fast- and slow-light regimes.7,13 In other words, do not yet invest in a faster-than-light communications system.
Acknowledgments
The authors gratefully acknowledge the financial support of the DARPA Defense Sciences Office Slow-Light Program, and DJG, the hospitality of professor Jürgen Kurths of Universität Potsdam in Germany, where his portion of the article was written.
Meet the authors
Daniel J. Gauthier is the Anne T. and Robert M. Bass professor of physics and chair of the physics department at Duke University in Durham, N.C.; e-mail: [email protected].
Robert W. Boyd is the M. Parker Givens professor of optics and a professor of physics at the University of Rochester in New York; e-mail: [email protected].
References
1. R.W. Boyd and D.J. Gauthier (2002). “Slow” and “fast” light. In: Progress in Optics, Vol. 43. E. Wolf, ed. Elsevier, pp. 497-530.
2. R.L. Smith (August 1970). The velocities of light. AM J PHYS, Vol. 38, pp. 978-984.
3. S. Chu and S. Wong (March 1982). Linear pulse propagation in an absorbing medium. PHYS REV LETT, Vol. 48, pp. 738-741.
4. B. Ségard and B. Macke (May 1985). Observation of negative velocity pulse propagation. PHYS LETT A, Vol. 109, pp. 213-216.
5. A.M. Steinberg and R.Y. Chiao (March 1994). Dispersionless, highly superluminal propagation in a medium with a gain doublet. PHYS REV A, Vol. 49, pp. 2071-2075.
6. L.J. Wang et al (July 2000). Gain-assisted superluminal light propagation. NATURE, Vol. 406, pp. 277-279.
7. M.D. Stenner et al (October 2003). The speed of information in a ‘fast-light’ optical medium. NATURE, Vol. 425, pp. 695-698.
8. M.S. Bigelow et al (July 2003). Superluminal and slow light propagation in a room-temperature solid. SCIENCE, Vol. 301, pp. 200-202.
9. G.M. Gehring et al (May 2006). Observation of backward pulse propagation through a medium with a negative group velocity. SCIENCE, Vol. 312, pp. 895-897.
10. A. Einstein (1988). Relativity: The Special and the General Theory — A Clear Explanation that Anyone Can Understand. Gramercy.
11. L. Brillouin (1960). Wave Propagation and Group Velocity, Academic Press.
12. H. Jeong et al (April 2006). Direct observation of optical precursors in a region of anomalous dispersion. PHYS REV LETT, Vol. 96, 143901.
13. M.D. Stenner et al (2005). Fast causal information transmission in a medium with a slow group velocity. PHYS REV LETT, Vol. 94, 053902.