
In Search of the Optimal Objective for 157 nm
Several techniques improve the performance of objectives used in microlithographic resist development.
James E. Webb
In the never-ending quest for the optimal objective for microlithography wavelengths, engineers have worked on ways to improve the aberration and birefringence correction of 0.85-NA Newtonian objectives used in microlithographic resist development. Corning Tropel Corp. has built, tested, optimized and delivered two objectives to customers for use in Exitech microsteppers.
Although the first of these objectives was designed and built with some knowledge of the effects of intrinsic birefringence in optical calcium fluoride, it was before methods to reduce its impact could be implemented. Previous work discussed off-wavelength testing of this objective, the optimization of the lens wavefront using a 244-nm Twyman-Green interferometer
and the models that use these measurements to predict the performance at 157 nm.1
Birefringence models demonstrate that the intrinsic birefringence in the calcium fluoride optical components cause sufficient phase aberration to have a measurable effect on the wavefront at the wave- length of use. However, the amount of aberration does not have a significant impact on performance in resist imagery because this small-field objective has a much shorter optical path than a typical full-field production tool lens.
The second objective was built, tested and optimized using 244-nm interferometry and then optimized with 157-nm wavelength interferometry to measure the birefringence and improve the wavefront. These results were compared with the modeling predictions and the wavelength difference computed.
The design form
The company designed the 0.85-NA optical system for use at 157 nm in step-and-repeat cameras that are employed to form 15X reduced images of test patterns for microlithographic resist development with a variety of illumination conditions. The Newtonian design form incorporates single-crystal CaF2 as the refractive material for this wavelength. See the table for the first-order parameters for this lens.
This catadioptric form, which is a system that uses both reflection and refraction, combines a double Mangin mirror with a unique single on-axis beamsplitter and high-reflectivity primary mirror. This first refracts the light and then reflects it twice, folding the beam path and focusing the light through a hole in the coating of the primary mirror to a flat-image plane (Figure 1).
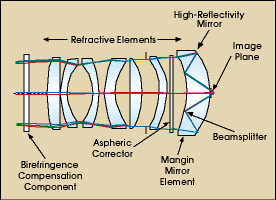
Figure 1. The 85-NA Newtonian objective uses both reflection and refraction.
This form is significantly different from others in the industry because the front group of elements has almost no refractive power and the two mirror reflections have most of the optical power. The maximum marginal ray angles are much larger than those achievable in any all-refractive design.
Comparisons
Before the arrival of 157-nm interferometers, the first Newtonian objectives used off-wavelength null optics. The objective and null lens combinations are tested at 244 nm in a Twyman-Green interferometer, and the measured wavefronts are fitted to Zernike polynomials.1 Analysis of the fitted Zernike terms helps pinpoint changes needed to the optical system for optimal performance at 157 nm (Figure 2a). These corrections are achieved by modifying the surface of an aspheric plate in a closed-loop optimization process.

Figure 2. In (a), the objective and null lens combination is tested at 244 nm in a Twyman-Green interferometer, and the measured wavefronts are fitted to Zernike polynomials. In (b), the null optics are removed and the objective inserted into the 157-nm interferometer and illuminated with unpolarized light. Zernike wavefronts are constructed from the measured data and compared with the 244-nm measurement. In (c), final improvements are made to the lens by modifying the surface of the aspheric corrector plate based on 157-nm measurements. (TIR = total internal reflection)
The success of this improvement process depends upon the accuracy of the null optics used to cancel the spherochromatic errors created when testing the objective at 244 nm. The initial wavefront error measured 30 nm rms. Two correction passes reduced the wavefront error to 6 nm rms. Although more improvements were possible, it was decided that further correction to the wavefront should be based on interferometric tests at 157 nm.
After the null optics have been removed, the objective is inserted into the 157-nm interferometer and is illuminated with unpolarized light. It must first be set to the correct conjugates, which are determined by measuring the reduction ratio. When the reduction errors are less than 30 ppm, Zernike wavefronts are constructed from the measured data (Figure 2b).
Comparison of wavefronts between 244- and 157-nm interferometer tests provides valuable information about CaF2 crystal behavior for different wavelengths. The wavefronts measured at each wavelength travel nearly identical paths through 112 mm of glass path at varying cone angles through the crystalline material. The two wavefronts are very similar in both shape and magnitude, particularly the larger low-order asymmetric Zernike terms. Careful examination of the difference between them reveals a small 3-theta wavefront residual that is related to the anisotropic nature of the material at 157 nm and predicted by the model. The final improvement made to the lens is based on 157-nm measurements (Figure 2c).
Intrinsic birefringence
Birefringence is the difference in optical path for two orthogonal polarizations of light passing through a material. Researchers at the National Institute of Standards and Technology (NIST)2,3 have measured and predicted intrinsic birefringence in cubic crystals at wavelengths below 200 nm, including CaF2, as small but relevant orientation- and polarization-dependent changes in index of refraction. The material thus has a small optical anisotropy.
The NIST measurements and theoretical predictions were implemented in Code V software from Optical Research Associates of Pasadena, Calif.4 With this software, Corning engineers were able to model this aberration and devise a unique method to reduce its effects. The majority of the intrinsic birefringence error accumulates in the last two passes through the double Mangin element. The total accumulated intrinsic birefringence is a low-order radially symmetric phase error combined with a smaller 3-theta higher-order asymmetric residual. Introducing a radial birefringent compensator significantly reduces the intrinsic birefringence.
Wavefront measurement techniques that quantify wavefront and birefringence errors at 157 nm in both magnitude and direction are required to validate the models and the methods for reducing them. To make meaningful wavefront measurements at 157 nm, typical interferometer designs and data-analysis algorithms must be modified. Linearly polarized light is used to obtain measurements of the wavefront and the polarization-dependent phase error information caused by birefringence.
By rotating an analyzer, data is collected at a field point for a range of polarization orientations and is used to construct two polar-orthogonal polarization wavefronts for characterizing lens performance. The difference in these two wavefronts is used to quantify the intrinsic birefringence. This birefringence map is compared with the model predictions from the software. The modeled and measured intrinsic birefringence maps (Figures 3a and 3b) for this objective are strikingly similar in both magnitude and shape, further validating the measurements and theoretical models used, and the numerical value of the intrinsic birefringence in CaF2 presented by NIST.
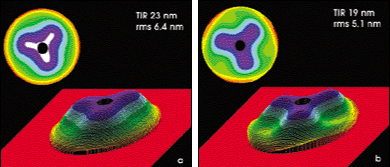
Figure 3. With these birefringence maps of the objective, engineers were able to compare the modeled version (a) produced by Code V software with the measured version (b) to determine the intrinsic birefringence. The maps are similar in shape and magnitude.
Further optimization of this design can be accomplished by inserting a radial birefringent compensation element into the lens. The same modeling code is used to determine the optimal location and thickness that reduces the birefringence in the assembly. The part is inserted into the assembly and adjustments are made. Again, data is collected and used to construct the birefringence map, which is compared with the model predictions (Figures 4a and 4b). The radial component of the intrinsic birefringence caused by CaF2 can be eliminated from the model and is minuscule in the measured data.
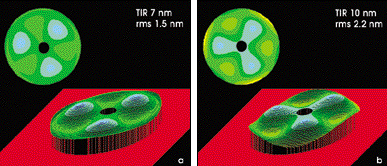
Figure 4. After inserting a radial birefringence compensation element into the lens and comparing the modeled (a) and measured (b) birefringence maps, it was determined that the radial component of the intrinsic birefringence that is caused by the calcium fluoride can be eliminated in the model and is insignificant in the measured data.
The results are in
Comparisons between 244- and 157-nm measurements show similar wavefronts but sufficient difference to warrant final correction based on 157-nm data. Modification has decreased the residual error to 3.1 nm rms (0.019 wave rms). The effects of the intrinsic birefringence in CaF2 on the Newtonian design are predicted to have both a radial and 3-theta residual term. A measurement technique that has been developed to quantify this error shows close agreement to the predictions. Inserting a radially birefringent material into the assembly reduces the errors caused by the intrinsic birefringence, and measurements confirm the predicted improvement.
References
1. J.E. Webb et al (2002). Performance enhancement of 157nm Newtonian catadioptric objectives. Proc. SPIE, Optical Microlithography XV, pp. 626-636.
2. J. Burnett et al (2001). Intrinsic birefringence in 157nm materials. Sematech Calcium Fluoride Birefringence Workshop.
3. J. Burnett et al (2001). Intrinsic birefringence in calcium fluoride and barium fluoride. PHYSICAL REVIEW B, Vol. 64, 241102(R).
4. H. Schreiber et al (2002). 157nm system test for high NA lithographic lens systems. Proc. SPIE, Optical Microlithography XV, pp. 1675-1685.
Meet the author
James E. Webb is optical design manager at Corning Tropel Corp. in Fairport, N.Y. He received a BS in physics and optics from Rochester Institute of Technology in 1977.
/Buyers_Guide/Corning_Tropel_Corp/c3075