New architecture could enable simultaneous monitoring of millions of neurons in 3D space at frame rates limited only by image sensor read times.
NICK ANTIPA, GRACE KUO, AND LAURA WALLER, UNIVERSITY OF CALIFORNIA, BERKELEY
Understanding brain function at the scale of individual neurons could open the door for advanced understanding of animal and human behavior and the mechanisms of neurological disorders such as Alzheimer’s. But the size scale of neurons and their extremely large numbers create an extreme imaging challenge.
Calcium imaging enables optical monitoring of the action potential of individual neurons, resulting in maps of neural circuitry in living brains. To achieve this, calcium-sensitive fluorescent indicators are introduced into the neurons of a live animal. The indicators change configuration when they bind to calcium, which is released by voltage-gated channels on the cell membrane when a neuron activates. This causes the fluorescent indicators to light up temporarily when the neuron fires. Recording many optical images per second results in a complete view of the calcium levels within individual neurons, providing an in-depth look at the electrical activity.
The speed and scale requirements of imaging neural activity brainwide presents significant challenges for designing optical devices and algorithms.
Mammalian brains have millions to billions of neurons that are tens of micrometers in size and distributed over a relatively large volume. A mouse brain, for example, is approximately 1 cm in diameter and can contain up to 75 million neurons. Until recently, neuroscientists have relied on techniques that either image a small region of the brain at high resolution1,2 or monitor the entire brain with resolution significantly less detailed than neuron scale, such as through functional magnetic resonance imaging (fMRI)3. Furthermore, for an animal to move freely while being monitored, the optical devices need to be small enough to implant without excessively encumbering the animal’s movement. To image large numbers of neurons, the devices must have a very large field of view (FOV). The systems also should be able to distinguish neurons that are axially aligned but at distinct depths. Using coded aperture imaging techniques, a new class of lensless computational imaging systems may enable compact, implantable systems capable of optically monitoring extremely large numbers of neurons in vivo.
Light-field microscopes using specialized algorithms have been used for fast 3D neural activity monitoring4. However, these large benchtop microscopes are difficult to miniaturize and implant while achieving whole-brain FOV5. For example, a 2.5×, 0.08-NA objective can image a 10-mm mouse brain with 4-µm resolution. But such an objective is typically more than 30 mm in diameter and 40 mm long — much too bulky to attach to a freely moving mouse.
Some strides have been made in miniaturizing objectives by using gradient index lenses6. These systems have an FOV of much less than a millimeter — far from a whole-brain scale. For certain experiments, this may not be a limitation. However, for implanting into living animals, traditional lens-based approaches will always run into fundamental physical constraints. In an effort to mitigate this, a more compact imaging architecture is needed.
Instead of a lens, a single thin optical element is placed between the sample and the sensor. The optic is designed such that each point within the volume casts a unique and identifiable pattern.
In a traditional lens-based imaging system, a point in the sample maps to a point within the camera body. In contrast, lensless imagers do not rely on lenses to form the image. Instead, a single thin optical element is placed between the sample and the sensor7,8.
The optic is designed such that each point within the volume casts a unique and identifiable pattern on the sensor, similar to coded aperture. It is then possible to compute the locations and brightness of a large number of points within the sample, all from a single 2D measurement.
The benefits of this are twofold.
First, the architecture offers a path to extremely small cameras — the mask is typically less than 1 mm thick, and the FOV is limited primarily by the sensor dimensions. A large FOV can be realized simply by using a larger chip, which does not necessitate increasing the system thickness.
Second, lensless architecture can capture depth information for samples close to the mask. The technology could enable simultaneous monitoring of millions of neurons in 3D space at frame rates limited only by image sensor read times. This is more than fast enough to keep up with neuron dynamics.
Recently, researchers at the University of California, Berkeley demonstrated a lensless camera (DiffuserCam) that images in 3D8 (Figure 1). It uses a pseudo-random smooth phase mask, called a diffuser, to encode 3D intensity information onto a 2D image sensor. A point source creates a pattern of high-contrast, high-frequency caustics on the sensor. This phenomenon is similar to the pattern on the bottom of a swimming pool on a sunny day.
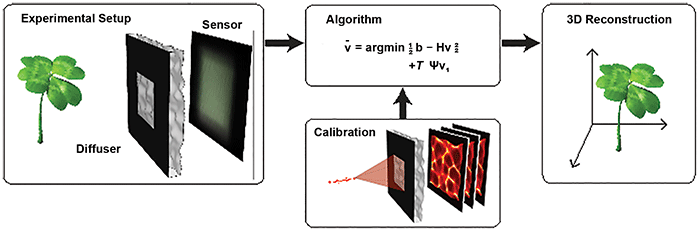
Figure 1. The DiffuserCam lensless imaging architecture consists of a diffuser placed in front of a 2D image sensor. When an object is placed in front of the diffuser, its volumetric information is encoded into a single 2D measurement. The system is designed so that calibration is simple and needs to be performed only once. Borrowing tools from the field of compressed sensing, the 3D image is reconstructed by solving a sparsity-constrained optimization problem. Courtesy of Optica/Nick Antipa and Grace Kuo.
With an appropriately chosen mask, each caustic pattern is unique to a location in 3D space. A single point then can be located easily, given knowledge of all possible caustic patterns the mask can produce. However, when multiple light sources are present, their subsequent caustics will superimpose on the sensor. It is then necessary to computationally disentangle the 3D location and brightness of all sources.
When imaging objects that possess a mathematical property known as sparsity, it is possible to recover the intensity distribution over a large 3D volume, all from a single 2D measurement.
This reconstruction is not always possible because of the extremely large number of possible locations for each light source. However, when imaging objects that possess a mathematical property known as sparsity — the object can be expressed using very few nonzero values — it is possible to recover the intensity distribution over a large 3D volume, all from a single 2D measurement.
A scene consisting of multiple fluorescent sources is an example of a sparse scene. Most of the space is dark because it is devoid of fluorophores, with light only radiating from the sources. The dark regions can be represented using zeros. Nonzero values are only needed to describe the intensity at voxels containing sources. The entire scene can be represented sparsely.
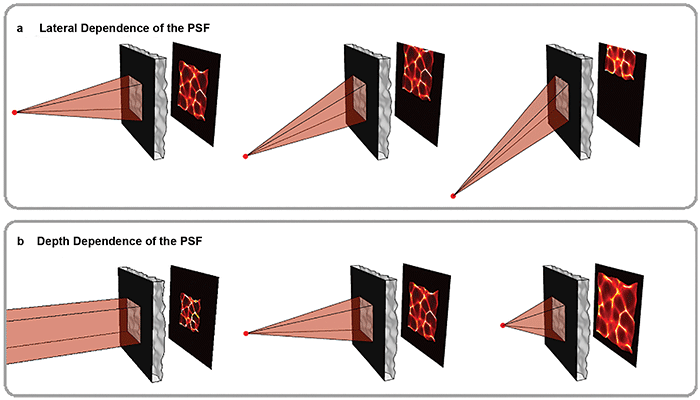
Figure 2. Volumetric information is encoded in pseudorandom patterns called caustics. As shown in the top panel, the mask is chosen so that the caustic pattern shifts as a point in the scene moves laterally, a key feature that enables imaging large volumes efficiently. The bottom panel shows how the pattern varies with depth. Because the pattern is pseudorandom, each point in 3D produces a unique and identifiable pattern. Courtesy of Optica/Nick Antipa and Grace Kuo.
For this method to work, the caustics created by any point within an FOV must be known. To reduce the number of possible patterns, a weak diffuser is used with an aperture. This leads to systematic behavior of the caustics. As the point moves laterally, the caustics simply translate across the sensor (Figure 2, top panel). By measuring just the on-axis caustics at a given depth, the off-axis patterns can be easily computed.
Varying patterns
As the point changes depth (for example, moves closer), the caustics approximately magnify, encoding depth information of the source (Figure 2, bottom panel). At a given depth, moving the point source laterally simply shifts the caustics across the sensor. This makes it easy to deduce all off-axis patterns at that depth from a single on-axis measurement, accelerating both computation and calibration (Figure 2, top panel).
The entire system can be calibrated by recording an image of a point source at each depth within the volume of interest, resulting in calibration sets containing only a few hundred images. In contrast, if every point in the volume needed to be measured, it would require hundreds of millions of images — nearly a petabyte of storage — to complete calibration.
Using this approach, an image of a sparse 3D object containing tens of millions of voxels can be computed from a single 1.3-MP 2D exposure (Figure 3). The frame rate is limited by the camera exposure, as this method can image a 3D volume using a single 2D image. Thus, it is possible to record activity over a large area at sufficiently fast frame rates for imaging neural dynamics. But there remains work to be done.
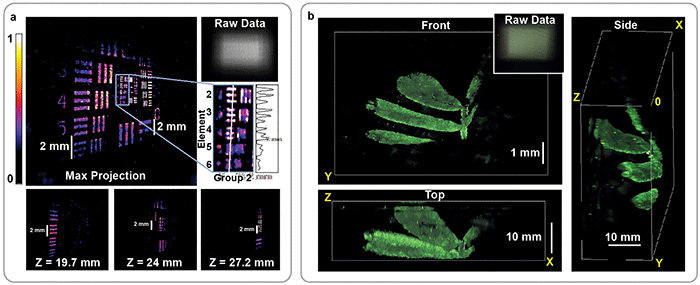
Figure 3. Reconstruction of fluorescent resolution target, tilted at an angle to the imaging system (a). 3D image of a small plant recorded by the DiffuserCam, rendered from multiple angles (b). In both cases, the 3D structure is recovered from a single 2D measurement. The corresponding 2D raw data is shown for each panel (upper-right insets). Courtesy of Optica/Nick Antipa and Grace Kuo.
For lensless cameras to image small objects such as neurons, the object must be placed close to the mask. But this presents a challenge for lensless cameras: Exhaustive calibration is not an option, so most lensless cameras are designed so that the system can be completely characterized using a tractable number of measurements.
For refractive masks, one way to do this is to impose a minimum object distance. This causes rays at the mask to behave paraxially, enabling both efficient calibration and image reconstruction. Unfortunately, it also limits the magnification and resolution of the final system to macro-scale scenes. To push the magnification and resolution to neuron scales, new masks and algorithms are being designed in tandem so that high ray angles can be used while maintaining algorithmic efficiency.
Currently, most lensless cameras make the assumption that light emitted by a point will travel in a straight line until it hits the camera, but inside the brain this assumption starts to break down. When emitted light interacts with other cell bodies and organelles, the light is scattered in unknown directions.
Light emitted near the surface of the brain probably won’t interact with scatterers before detection. In this regime, the current models hold well. But imaging neurons deeper in the brain requires the light to travel farther through tissue, and it will likely hit many scatterers on the way, reducing contrast and resolution.
One fix for this problem is to use imaging models that account for scattering. Including accurate scattering models in the reconstruction algorithm will ensure the best possible image. And since scattering causes a reduction in contrast, small amounts of noise can have a large impact on the reconstruction quality, even with accurate models.
Another method is to use longer wavelengths of light, which are less affected by scattering. The most widely used calcium indicator, GCaMP, emits green light. New red indicators have been developed9 that suffer less from scattering, which permits deeper imaging into the brain.
The next leap in neural imaging will necessitate time-resolved simultaneous measurement of the electrical dynamics of extremely large numbers of neurons. Calcium imaging has already proven a valuable technique in meeting these demands. Lensless cameras may offer the ability to see the complex dynamics that calcium imaging brings to light.
Meet the authors
Nick Antipa is a Ph.D. student at UC Berkeley. He has a bachelor’s degree in optics from UC Davis and a master’s in optics from the University of Rochester. He is currently researching the incorporation of advanced signal processing algorithms into optical imaging system design; email: [email protected].
Grace Kuo is a Ph.D. student in the Department of Electrical Engineering and Computer Science at UC Berkeley. She has a bachelor’s sington University in St. Louis; email: [email protected].
Laura Waller, Ph.D., leads the Computational Imaging Lab at UC Berkeley, which develops new methods for optical imaging, with optics and computational algorithms designed jointly. She holds the Ted Van Duzer Endowed Professorship and is a senior fellow at the Berkeley Institute of Data Science, with affiliations in bioengineering and applied sciences and technology; email: [email protected].
References
1. F. Helmchen and W. Denk (2005). Deep tissue two-photon microscopy. Nat Methods, Vol. 2, Issue 12, pp. 932-940.
2. F. Helmchen et al. (2001). A miniature head-mounted two-photon microscope: high-resolution brain imaging in freely moving animals. Neuron, Vol. 31, Issue 6, pp. 903-912.
3. S. Ogawa et al. (1990). Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U.S.A., Vol. 87, Issue 24, pp. 9868-9872.
4. N.C. Pégard et al. (2016). Compressive light-field microscopy for 3D neural activity recording. Optica, Vol. 3, Issue 5, pp. 517-524.
5. O. Skocek et al. (2018). High-speed volumetric imaging of neuronal activity in freely moving rodents. Nat Methods, Vol. 15, Issue 6, pp. 429-432.
6. K.K. Ghosh et al. (2011). Miniaturized integration of a fluorescence microscope. Nat Methods, Vol. 8, Issue 10, pp. 871-878.
7. J.K. Adams et al. (2017). Single-frame 3D fluorescence microscopy with ultraminiature lensless FlatScope. Science Advances, Vol. 3, Issue 12, p. e1701548.
8. N. Antipa et al. (2018). DiffuserCam: lensless single-exposure 3D imaging. Optica, Vol. 5, Issue 1, pp. 1-9.
9. H. Dana et al. (2016). Sensitive red protein calcium indicators for imaging neural activity. eLife, Vol. 5, p. e12727.