Holey fibers find application in nonlinear optics such as for continuum generation, in transporting high optical powers, and in sensors and tunable hybrid devices.
Anders O. Bjarklev, Danmarks Tekniske Universitet, and Jes Broeng, Crystal Fibre A/S
Holey fibers, in which airholes are introduced in the cladding region and extended in the axial direction of the fiber, have been known since the early days of silica waveguide research.1 Early work demonstrated the first low-loss fibers, which featured very small silica cores held in air by thin bridges of silica. But the technology of conventional, doped-silica fibers progressed rapidly, driven primarily by optical communications, and the holey fibers were not developed much further for a number of years.
Then, in 1996, fibers with a so-called photonic crystal cladding were demonstrated.2 The field of photonic crystal fibers was founded, with the realization of microstructured silica fibers that featured a periodic array of airholes running their length.3
The initial aim was to fabricate fibers that could guide light using photonic bandgap effects.4 However, it soon was realized that light guiding in the first holey fibers was based on total internal reflection, because the index of the core was higher than the effective index of the cladding. Despite their resemblance to conventional optical fibers, the index-guiding photonic crystal fibers (Figure 1) display optical characteristics not found in their conventional counterparts.

Figure 1. This typical large-mode-area photonic crystal fiber has a 15-μm core and a triangular lattice of airholes in the cladding.
High nonlinearity
One such characteristic of these microstructured fibers involves their ability to confine light in a very small cross-sectional area through the use of high-index contrast between holes and glass. This is the concept behind highly nonlinear photonic crystal fibers, which have applications in fields ranging from spectroscopy and sensing to telecommunications.
Their high nonlinear coefficient and designable dispersion properties make these fibers attractive for many nonlinear applications, of which supercontinuum generation has been the most intensively investigated.5 The continua have been used in optical coherence tomography, spectroscopy and metrology. Considerable effort has been made to better comprehend the complex interplay of nonlinear processes behind supercontinuum generation, and many of the basic mechanisms — e.g., soliton fission, self-phase modulation, four-wave-mixing and stimulated Raman scattering — are understood.6,7
The key to the success of photonic crystal fibers in nonlinear applications is not that silica is a highly nonlinear material — it isn’t — but that even modest optical powers can be concentrated to high intensities within the core because the index contrast between the silica core and air-filled cladding is so great. This results in highly effective nonlinearity per unit length, and thus it becomes feasible to reduce device lengths and the associated optical power requirements for fiber-based nonlinear devices.
When evaluating the advantages of small-core photonic crystal fibers, it is as important as the nonlinear coefficient that the fibers exhibit unique dispersive properties. By modifying the microstructure pattern, both the magnitude and the sign of the dispersion can be tailored to suit a particular application. The fibers can exhibit anomalous dispersion down to a wavelength of 550 nm, which has made soliton generation in the near-IR and in the visible possible.
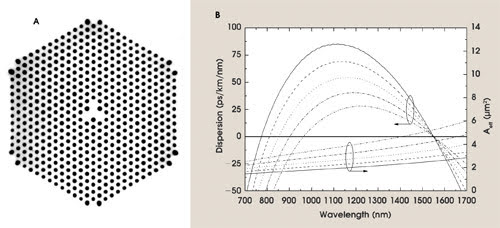
Figure 2. This complex, highly nonlinear photonic crystal fiber has a 120° symmetry, a core whose center is germanium-doped silica, and three solid elements surrounding the core that are fluorine-doped to adjust the dispersion (a). Corresponding dispersion and effective area values as function of wavelength are presented for a number of dimensions for the highly nonlinear fiber (b).
An advanced microstructure design has demonstrated simultaneous control of nonlinearity and near-zero dispersion at telecom wavelengths.8 A micrograph of the fiber in cross section reveals 13 layers of microscopic holes surrounding the core (Figure 2a). The core itself is formed by a center element, which is up-doped to a higher refractive index by germanium.
These solid regions placed symmetrically around the circumference of this center element are down-doped with a fluorine codopant.
This complex fiber structure enabled the dispersion control indicated in Figure 2b, which shows the dispersion and effective-area values as a function of wavelength for different fibers having the basic design shown in Figure 2a. By adjusting the hole-to-hole spacing, a fiber with zero dispersion at 1.55 μm and an adjustable dispersion slope was created.
Confinement losses rise
As indicated in the figure, the hole-to-hole spacing also determines the effective mode area in the fiber. Although the fiber’s intensity increases with decreasing mode area, confinement losses rise as well. Another parameter in the design of the microstructure is the air-filling fraction, and increasing this parameter decreases confinement losses without changing the effective mode area. Adding more rings of holes around the core also reduces confinement loss.
With careful design, fibers with small core areas (less than 2 μm2) and low confinement loss (less than 0.2 dB/km) can be fabricated. Because they are highly nonlinear, relatively short lengths of less than 10 m are required for most applications, so confinement losses on the order of 1 dB/km can be tolerated easily.
At the opposite end of the applications spectrum from such highly nonlinear photonic crystal fibers, large-mode-area fibers are designed to suppress nonlinearities in fibers that transport high optical powers. In many cases, spatial mode quality is also a critical issue, and fibers that support only a single transverse mode are preferable.
Conventional single-mode fibers can be fabricated with relatively large modes by simultaneously increasing the core diameter and decreasing the numerical aperture. (The numerical aperture shrinks as the difference between the refractive indices of the core and cladding shrinks.) The ultimate limitation, however, is imposed by the precision with which the refractive indices can be controlled. As a practical matter, conventional fiber cannot readily be fabricated with a numerical aperture of less than ~0.06, while photonic crystal fibers with a numerical aperture of 0.03 and lower can be fabricated by carefully controlling their microstructure.
A microstructure commonly employed in large-mode-area photonic crystal fibers is a triangular array of holes, with one hole missing at the center to provide the core. These fibers are fabricated by stacking many hollow capillaries with a solid rod at the center to create a preform and by drawing the preform into a fiber in a standard drawing tower. Such a fiber is sometimes called a single-rod photonic crystal fiber, and so long as the ratio of the airhole diameter to the hole-to-hole spacing (d/Λ) is less than 0.45, the fiber is endlessly single-mode; that is, it can support only a single mode, no matter how large the core.
Losses increase
As a practical limit, however, as the core becomes larger and larger while maintaining the d/Λ required for single-mode operation, the ratio of the wavelength to the hole-to-hole spacing becomes much less than 1. In this limit, the index of the core approaches that of the cladding, and losses due to macro- and microbending increase. For large-mode-area photonic crystal fibers in the ultraviolet and visible regimes, this sets an upper limit on the mode areas that can be realized with a reasonable loss.

Figure 3. Unlike the fiber in Figure 1, which was drawn from a preform with a single solid rod at the center, this photonic crystal fiber was drawn from a preform with three solid rods. Thus, the core is formed by theabsence of three airholes, rather than one.
Even larger mode areas can be achieved in multirod photonic crystal fibers; that is, fibers where the core of the preform is formed by three or even more solid rods (Figure 3).9
Conventional fibers can function as sensors if part of the cladding is stripped away so that the material being sensed can interact with the evanescent fields in the fiber. There are several drawbacks to this approach, including the physical weakening of the fiber brought about by the removal of part of the cladding and the imprecision involved in controlling how much of the electric field interacts with the material.
These problems can be finessed by employing a photonic crystal fiber and allowing the material, in gaseous or liquid form, to fill the fiber’s airholes. The liquid possibility was explored recently.10 The research demonstrates a highly efficient evanescent-wave method for the detection of fluorophore-labeled biomolecules in submicroliter aqueous samples.
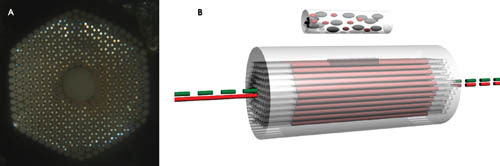
Figure 4. A micrograph shows the structure of a cross section of end-illuminated liquid-filled microstructured fiber (a). The light spots are effectively numerous suspended corelike structures in the cladding. A photonic crystal fiber filled with liquid crystal acts as an optically controlled lightmodulator (b).
The airholes of the fiber provide access for the sample to regions with a strong optical field. Figure 4a is a micrograph of such a microstructured fiber. Airholes with an average diameter of 3.4 μm are arranged in a triangular lattice with a 4-μm pitch. The cladding crystal provides a large number of air-suspended, index-guiding, corelike structures connected by thin silica bridges. Given the size of these structures, there is a strong penetration of the evanescent field into the sample for wavelengths in the visible range. The fraction of the optical field that propagates in the sample can be calculated and, in this case, turns out to be 5.2 percent for 650-nm light.
The chief advantage of the sensor is the minute amount of sample required for analysis. Although conventional techniques typically require several microliters of a liquid being analyzed, a 20-cm length of photonic crystal fiber can produce equally accurate results with submicroliter samples.
An interesting development involving similar hybrid microstructured fibers was the demonstration of an all-optical light modulator, in which a pulsed 532-nm laser modulated the spectral position of the bandgaps in a photonic crystal fiber infiltrated with a dye-doped nematic liquid crystal.11 A modulation frequency of 2 kHz was demonstrated for a pump power of only 2 to 3 mW.
In this experiment, the scientists at Danmarks Tekniske Universitet in Lyngby, Denmark, at Chalmers Tekniska Högskola in Göteborg, Sweden, and at Crystal Fibre A/S in Birkerød, Denmark, employed a large-mode-area photonic crystal fiber with a silica core surrounded by seven periods of airholes arranged in a triangular lattice. The hole diameter, hole pitch and core diameter were 3, 7 and 10 μm, respectively. The fiber was endlessly single-mode.
When the airholes were filled with a liquid crystal (Figure 4b) with a higher refractive index than that of silica, the fiber could no longer function as a normal photonic crystal fiber because the effective index of the cladding region was larger than the index of the core. Instead, it supported a finite number of guided wavelength bands because of antiresonant reflection from the liquid-crystal-filled holes. The alignment and refractive index of the liquid crystal and the structural parameters of the photonic crystal fiber determined the bandgaps’ spectral position.
Because the refractive indices of the liquid crystal were considerably higher than that of silica, the holes filled with liquid crystal formed isolated waveguides. The spectral position of the bandgaps became insensitive to the hole-to-hole spacing and was dominated by the features of the inner ring of holes surrounding the core.
And because the fiber’s geometric parameters were fixed in the manufacturing process, the bandgaps had to be tuned by changing the orientation and/or modifying the liquid crystal’s refractive indices.
These refractive indices can easily be tuned thermo-optically. To decrease the thermal response time compared with heating/cooling the entire fiber, the 532-nm pulsed laser was used to locally heat the liquid crystal filling the innermost ring of holes surrounding the core. The heating efficiency was increased when there was a high overlap between the core mode and the inner ring of cladding holes, achieved by doping the liquid crystal with a dye that had an absorption peak around 502 nm.
Meet the authors
Anders O. Bjarklev is a professor of optical communications at Danmarks Tekniske Universitet in Lyngby, Denmark; e-mail: [email protected].
Jes Broeng is a development engineer at Crystal Fibre A/S in Birkerød, Denmark; e-mail: [email protected].
References
1. P.V. Kaiser and H.W. Astle (1974). Low-loss single-material fibers made from pure fused silica. BELL SYST. TECH. JOURN., pp. 1021-1039.
2. J.C. Knight et al (October 1996). All-silica single-mode optical fiber with photonic crystal cladding. OPT. LETT. pp. 1547-1549.
3. A. Bjarklev et al (2003). Photonic Crystal Fibers. Kluwer Academic Publishers.
4. T.A. Birks et al (Oct. 26, 1995). Full 2-D photonic bandgaps in silica/air structures. ELECTRON. LETT., pp. 1941-1943.
5. J.K. Ranka et al (January 2000). Visible continuum generation in air silica microstructure optical fibers with anomalous dispersion at 800 nm. OPT. LETT., pp. 25-27.
6. S. Coen et al (April 2002). Supercontinuum generation by stimulated Raman scattering and parametric four-wave mixing in photonic crystal fibers. J. OPT. SOC. AM. B, pp. 753-764.
7. J. Herrmann et al (April 29, 2002). Experimental evidence for supercontinuum generation by fission of higher-order solitons in photonic fibers. PHYS. REV. LETT., 173901.
8. K.P. Hansen (June 30, 2003). Dispersion flattened hybrid-core nonlinear photonic crystal fiber. OPT. EXPRESS, pp. 1503-1509.
9. N. Mortensen et al (March 2003). Improved large-mode-area endlessly single-mode photonic crystal fibers. OPT. LETT., pp. 393-395.
10. J. Jensen et al (September 2004). Photonic crystal fiber based evanescent-wave sensor for detection of biomolecules in aqueous solutions. OPT. LETT., pp. 1974-1976.
11. T.T. Larsen et al (Oct. 6, 2003). Optical devices based on liquid crystal photonic bandgap fibres. OPT. EXPRESS, pp. 2589-2596.