Deep learning helps to unscramble signal information received from thousands of channels known as spatial fiber modes.
Eirini Kakkava, Babak Rahmani, Christophe Moser, and Demetri Psaltis École Polytechnique Fédérale de Lausanne (EPFL)
Single-mode optical fibers are well known for revolutionizing high-speed telecommunications. Due to their low loss, they transport information encoded in light for kilometers-long distances. A single-mode fiber carries just one spatial mode — but at a very high modulation rate. The ever-increasing volumes and data-transmission speeds required by various industries, such as telecommunications and medical instrumentation, are creating demand for multimode fiber, which provides multiple spatial channels in the same fiber conduit.

A conceptual image of a neural network being trained to project images through multimode fiber. Courtesy of EPFL.
In the last decade, researchers have begun to use multimode fiber for a different purpose than transmitting digital binary signals (ones and zeros). Namely, they have used it for sending analog (or grayscale) images. Multimode fiber supports thousands of independent information channels, known as spatial fiber modes, thus allowing for the delivery of complex signals such as analog images. What hindered the use of multimode fiber for transporting analog images from one end of the transmission line to the other, until recent years, was that the information contained in the image, though preserved, was scrambled at the output. This happens due to the various propagation velocities of each spatial mode through the fiber length, which causes randomization of the local amplitude and phase information of the input, until it reaches the output, where distortion occurs (Figure 1). If a correspondence — that is, a function — could be found between the scrambled output and the original image, the latter could be retrieved by applying the transformation function to the scrambled output.

Figure 1. Simulations show the propagation of an image of the number 5 through a multimode fiber with a 25-µm-core diameter and a 0.1 numerical aperture, at various distances from the fiber facet. Courtesy of EPFL.
It turns out that deep neural networks (DNNs), among other techniques, are very good at learning this function.
Several algorithms, both optical and computational, have been employed to compensate for the modal scrambling of the information traveling through multimode fiber. The aim has been to exploit the full potential of the fiber for imaging, sensing, and light-delivery applications employed in both telecommunications and medical instrumentation.
Almost all optical methods use a calibration process in which, for the fiber’s input, the output field is recorded and both its phase and amplitude information are saved1. In this way, the transmission matrix of the system can be constructed. And by taking advantage of the reversibility of the information randomization, the inverse transmission matrix calculation can provide full control over the light propagation and provide enough information to retrieve the desired optical field through multimode fibers. This method — called the “transmission matrix method” — together with other optical holographic techniques, such as phase conjugation, has shown promising results. Nevertheless, complex optical setups are required for such measurements, and they come with the additional risk that external perturbations (outside movements or forces) could invalidate the whole calibration.
However, iterative optimization methods (clustering) have also shown interesting results in controlling the light. Optimization techniques use the idea of projecting patterns through a fiber while monitoring the error value between the wanted result and the one recorded at the fiber’s end. By slightly changing the input patterns, the algorithm attempts to minimize this error. One drawback of this method is that the optimization process must be repeated for every new desired output readout, which slows down the speed. As a result, a robust method to read and control the information delivered through these fibers is of constant scientific and industrial interest — and solving this problem would be a pivotal step in increasing information throughput.
The advancement of computational means, especially that of graphics processing units, has enabled the use of deep neural networks to analyze and respond to large amounts of data in various technological fields, including fiber optics. Deep neural networks are algorithms that are inspired by the way the human brain transforms a signal into useful information. Therefore, the complexity of signal processing by a deep neural network, and the nonlinearity of the information recovery/control through deep learning enables complex mapping strategies, from raw measurements to high-level representations.
In fact, the authors have shown in previous work that deep neural networks could be successfully trained to reconstruct, classify, or project various images (with amplitude and/or phase features) through multimode fibers. Thanks to their nonlinear character, deep neural networks do not require detailed measurement of the field at the fiber output, contrary to holographic methods, but they can infer relevant information from intensity-only images of the corresponding speckle to an input image2,3. Therefore, the experimental apparatus for the data set acquisition becomes significantly simpler.
The training data set consists of thousands of image pairs: input images obtained from the Modified National Institute of Standards and Technology database of handwritten digits and their corresponding speckle pattern intensity images recorded after propagation through a multimode fiber. Image classification, along reconstruction from images of speckle patterns, is then performed by training a VGG-type DNN classifier and a Unet-type reconstruction DNN, respectively. Remarkably, a 90% reconstruction efficiency of images and a 70% classification accuracy were obtained after the relevant DNN processed the corresponding speckle patterns2.
These results have been reported for up to 1-km-long multimode fibers (Figure 2). When examining the outcome in context, the stability of the system needs to be considered. Environmental perturbations severely affect the propagation of light through multimode fibers, causing random speckle drifts. For calibration-based techniques such as the transmission matrix method, disturbances of this kind invalidate the measurement. Nevertheless, the deep neural networks were able to overcome the noise in the data, demonstrating high robustness.
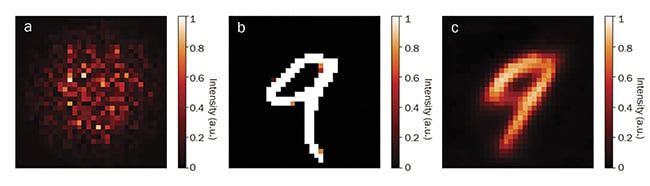
Figure 2. Deep learning in the example of multimode fiber input. The speckle pattern output of the fiber when the input image (a) has propagated through the 1-km-long fiber (b), and the deep neural network reconstruction (c) is receiving (a) as an input. Courtesy of EPFL.
Training neural networks for reconstructing or classifying images propagated through the multimode fiber is a supervised learning method, meaning that a set of input patterns and their corresponding labeled outputs are used to train the network. Then, it is expected that the network could show some level of generalization in reconstructing and classifying images that are similar to the ground truth images (examples of the desired target output and their corresponding input patterns). For some applications, such as projecting arbitrary images through the fiber, the required control pattern that is needed to project the images at the distal side of the fiber is not known a priori. In other words, no ground truth data is available with which to train a neural network.
Using two networks for emulating the forward and backward paths of the fiber has proved successful for alleviating the lack of ground truth examples for control applications. A model network could be used to learn to map the input patterns of the fiber to their output patterns4. The second network (the actor network), mimicking the backward path, is tasked with finding the required input pattern that results in the projection of the desired target output. The actor network learns to find such a pattern by sending its proposed output through the model network and comparing the result with the desired target pattern that the actor network was initially fed, effectively making a closed-loop training.
Iteratively training both networks a number of times helps to increase the fidelity of the projected images. Additionally, because both networks are constantly retrained with new examples from the multimode fiber system, any perturbation altering the system, such as temperature change or mechanical instability, is automatically picked up and learned by the networks. Training with examples of the latter makes this imaging method robust to perturbations and changes incurred upon the system. Figure 3 shows examples of images projected through a 50-µm-core-diameter, 75-cm-long step-index multimode fiber for red, green, and blue colors, together with a superimposition of all three.
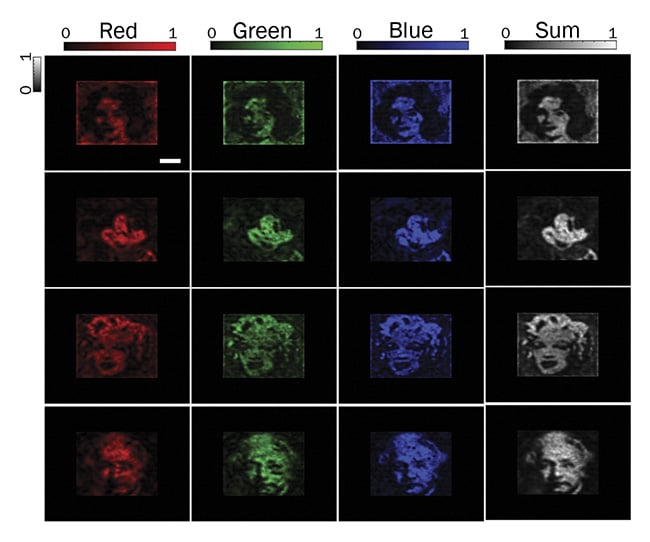
Figure 3. Images projected through a multimode fiber via a two-network method. Adapted with permission from Reference 4.
The resilience of deep learning for recovering information through multimode fiber has also been validated for other noisy situations, such as the change of bending configuration and the presence of wavelength fluctuations of the light source. In particular, the bending sensitivity of multimode fiber has been a major issue to solve. It is currently under study by Tomas Cizmar’s group at the Leibniz Institute of Photonic Technology and others in the research community because this sensitivity prevents the use of multimode fiber for image delivery. Data acquisition in the presence of noise (bending or wavelength changes) has been shown to assist the deep neural network performance for recovering the fiber input and its generalization5,6.
Apart from reading and controlling the information received through multimode fibers, deep learning has also been used for studying the way light propagates in terms of modal decomposition and temporal evolution. Modal decomposition was achieved by training the deep neural networks with synthetic data. Since the mode solutions for multimode fiber can be analytically calculated, thousands of examples were generated by simulating the propagation of thousands of beam intensity profiles. Then the examples were analyzed into the supported spatial modes with certain weights7. The deep neural networks showed impressive results when tested both on the synthetic and experimental data. In the case of temporal evolution, deep learning was used to characterize the amplitude and the phase of a pulse through a multimode fiber8.
Finally, it is widely accepted that deep learning opens paths for advanced scientific and industrial development, pivoting information delivery and control via guiding light through multimode fiber. Optical computing, augmented reality, and medical instrumentation are some of the photonics industry fields that can greatly benefit from the application of AI.
Meet the authors
Eirini Kakkava, Ph.D., received a doctorate in photonics from the École Polytechnique Fédérale de Lausanne (EPFL) in Switzerland. During her doctoral studies in EPFL’s Optics Laboratory, she developed optical and computational methods for endoscopic imaging.
Babak Rahmani is a doctoral student at EPFL, where he is studying computational imaging and the application of machine learning for solving inverse problems.
Christophe Moser is a professor in the Institute of Microengineering at EPFL and heads its Laboratory of Applied Photonics Devices.
Demetri Psaltis is a professor in the Institute of Microengineering at EPFL and heads its Optics Laboratory.
References
1. E. Kakkava et al. (2019). Selective femtosecond laser ablation via two-photon fluorescence imaging through a multimode fiber. Biomed Opt Express, Vol. 10,
Issue 2, pp. 423-433.
2. N. Borhani et al. (2018). Learning to see through multimode fibers. Optica, Vol. 5, pp. 960-966.
3. B. Rahmani et al. (2018). Multimode optical fiber transmission with a deep learning network. Light Sci Appl, Vol. 7, Article no. 69.
4. B. Rahman et al. (2020). Actor neural networks for the robust control of partially measured nonlinear systems showcased for image propagation through diffuse media. Nat Mach Intell, Vol. 2, pp. 403-410.
5. P. Fan et al. (2019). Deep learning the high variability and randomness inside multimode fibers. Opt Express, Vol. 27, Issue 15, pp. 20241-20258.
6. E. Kakkava et al. (2020). Deep learning-based image classification through a multimode fiber in the presence of wavelength drift. Appl Sci, Vol. 10, p. 3816.
7. Y. An et al. (2020). Deep learning-based real-time mode decomposition for multimode fibers. IEEE J Sel Top Quantum Electron, Vol. 26, pp. 1-6.
8. W. Xiong et al. (2020). Deep learning of ultrafast pulses with a multimode fiber. APL Photonics, Vol. 5, p. 096106.