Whether the simulation involves grenade launchers or inert mines, laser technology allows military personnel to train more effectively.
David Page, Precision-Optical Engineering
Paintballing techniques are well-established military training tools, but by using laser simulation devices, one can “paintball” with light. To make the training as representative as possible of the dangers to be found on the battleground, the simulation devices must closely match the operating modes of the real devices. This was the challenge faced by Precision-Optical Engineering of Hitchin, UK, in developing lenses for laser simulation devices required by the former Royal Ordnance factory at Blackburn, UK.
Training exercises in woodland areas required two very different systems. The first was a grenade launcher simulator. A laser beam had to be projected down a corridor 450 meters long and 14 meters wide with sufficient energy within the corridor to trigger detectors on badges worn by personnel, but with an energy distribution such that detectors outside the corridor would not be triggered. The second device was a simulator of an inert mine that operates through a 60° angle over a distance of 50 meters. Again, the laser light had to be capable of triggering detectors within this range but not outside.
Laser profile
Because it would be necessary to manufacture each simulator system in quantities in excess of several hundred, the ease and cost of production of the optics were also significant factors.
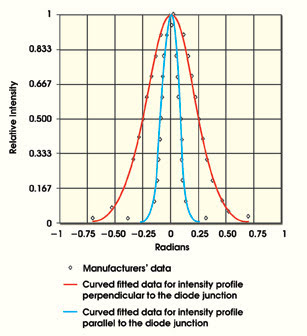
Figure 1. Both a grenade launcher and an inert mine simulation system paintball with light using a three-junction laser with intensity profiles parallel and perpendicular to the junction.
The laser used in both systems is a three-junction device with profiles parallel and perpendicular to the junction (Figure 1). To simplify the design process, engineers fitted curves to the intensity profiles to allow ready calculation of intensities. For the direction perpendicular to the junction, it is possible to fit a pure Gaussian curve:
I = ex(aq)2
where a is the fitted coefficient (–0.0033) and q is the angle of emission in degrees.
The fit for the profile parallel to the laser junction is quite different:
I = S [aiexp (aF2i)]
where F is the emission angle in degrees, a = –0.0315, a1 = 0.4029, a2 = 1.9142 and a3 = 21.344.
The intensity at any angle is given by:
I = exp(aq)2S [aiexp (aF2i)]
Because orthogonal Gaussian profiles cascade to produce intensities at compound angles that are simply the product of the two independent profiles, it is possible to reduce the lens design process from a full three-dimensional analysis to two two-dimensional designs.
Lens design concepts
The original plan was to use a combination of molded acrylic lenses and off-the-shelf glass cylindrical lenses. The acrylic lenses were designed with circularly symmetric aspheric optics that, when molded with radial injection, would maintain that symmetry, thereby overcoming deficiencies in the molding process by simply refocusing the system. The glass lenses were to be used to overcome the asymmetry in the emitted beam in the case of the grenade launcher simulator or to enhance the asymmetry in the case of the inert mine simulator.
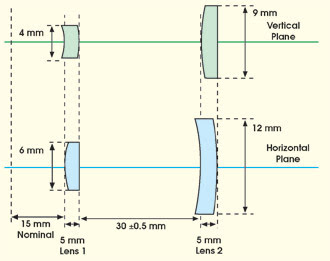
Figure 2. In a grenade launcher simulator developed by Precision-Optical Engineering, designers used this optical system configuration to project a laser beam down a 450-m-long, 14-m-wide corridor with sufficient energy to triggerdetectors within the corridor without triggering those outside the corridor.
Unfortunately, the lens molding industry was unable to produce these acrylic lenses in the quantities required at a reasonable cost. The solution was to manufacture the acrylic lenses using single-point diamond turning techniques.
This presented other design possibilities, so engineers were able to abandon the original centered aspheric/glass cylindrical lens combination in favor of using two acrylic toroidal lenses. This approach makes it possible to mount many lenses on the diamond turning lathe at any one time for mass production.
The toroidal design has a number of advantages. In particular, the effects of asymmetries in the horizontal and vertical profiles of the laser beam, the required output beam or both can be treated independent of one another. By considering that there is a horizontal plane through the lens system, engineers can design one of the lenses to behave like a window and have no effect on the beam. The other lens, however, has an aspheric profile, which is itself toroidal and is designed to manipulate the beam intensities from the laser beam to match the required intensity profile as closely as possible.
Just the reverse happens in the vertical plane through the lens system. The other lens now acts as a window, while the first lens has its own aspheric profile. Thus, designers can treat the two directions independently.
As part of the design process, new software was developed using an interactive Symbolic Processor (Mathcad 3.1) to allow ray tracing of the optical system from a source of given angular emission to provide a different angular emission profile. The process involves tracing two rays with just 0.001-radian separation from the laser source through the optical system and then out into target space. One can not only determine the look angle of the beams to show where they are heading in the required profile, but also calculate the change in angular separation, which in turn is used to calculate the intensity in the look angle direction.
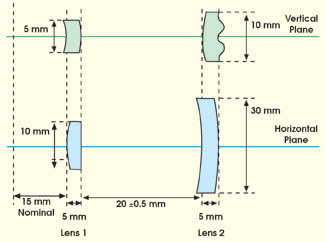
Figure 3. In this optical system for an inert mine simulator that operates through a 60° angle over a distance of 50 m, the laser light must be able to trigger detectors within this range but not outside it.
Solid angle changes
The design process is resolved into the horizontal and vertical planes, so one can assume that the intensity changes vary linearly with magnification because the solid angle into which the radiation projects changes in only one dimension. In fact, the crossed toroids mean that the solid angle does change in both dimensions, but that the effect on the horizontal intensity profile due to magnification is constant along the horizontal profile.
The threshold irradiance level for the detection system is 4.9 μJ/m2. Knowing the limiting range vs. angle, one can generate the required intensity profile and integrate it to determine the total amount of energy per pulse to provide the required conditions. From the ray trace, it is possible to calculate the angular spread of rays that just satisfy the requirements in the horizontal and vertical directions, as well as the power requirements of the diode.
Grenade launcher simulators
Engineers used the procedures outlined above to design the grenade launcher simulator (Table 1). Because the lenses are toroidal, the data differs for the parallel and perpendicular directions. The base radius of curvature of the toroid is 200 mm, which allows fitting several lenses onto the lathe per cutting run in line with the production volume requirements.
 To meet the intensity profile requirements of the beam in the vertical direction without placing unreasonable demands on the power output of the laser diode, the intensity is limited as much as possible. The major part of the excess intensity profile is masked off at short range to prevent the Gaussian component from dominating the output at this distance. This arrangement allows maintaining the beam profile within the 14-m-wide, 450-m-long corridor, with the exception of a 400-mm excursion between 70 and 80 m.
To meet the intensity profile requirements of the beam in the vertical direction without placing unreasonable demands on the power output of the laser diode, the intensity is limited as much as possible. The major part of the excess intensity profile is masked off at short range to prevent the Gaussian component from dominating the output at this distance. This arrangement allows maintaining the beam profile within the 14-m-wide, 450-m-long corridor, with the exception of a 400-mm excursion between 70 and 80 m.
Mine simulators
The energy required from the diode on purely geometric terms is 3.6 μJ per pulse. With reflective losses of 3.87 percent at each surface and taking into consideration the presence of a prism for pointing and an external window for sealing the system, the total transmission is 73 percent. A laser output of 4.9 μJ is therefore required.
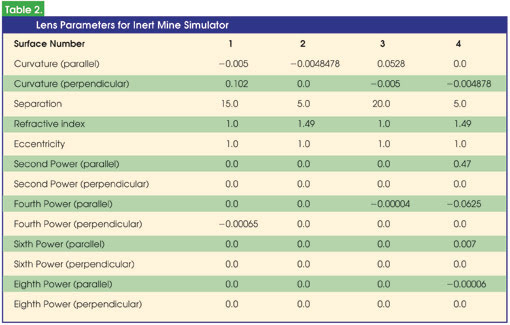
The required intensity profile for this system is asymmetric (Table 2). Engineers create the horizontal profile differently from other profiles because intensity must be uniform in the horizontal direction. To overcome inefficiencies introduced by using only a small part of the beam, they use a cyclical surface profile on the final surface. The first three optical surfaces combine to provide a collimated optical beam. The final cyclical surface then modifies the beam to project into the required 60° cone. The maximum slope of the surface prevents radiation from being refracted out of that cone.
 Modifications to the profile approximately divide a constant irradiance on a plane at 55 m and along an arc of radius at 55 m. The threshold range at the 30°-from-axis limit is 51.3 m. By repeating the profile on either side of the central profile, one increases the efficiency, which translates to the requirement for a pulse energy of 1.5 μJ. Taking reflection losses into account, this results in a need for 1.9 μJ per pulse from the laser.
Modifications to the profile approximately divide a constant irradiance on a plane at 55 m and along an arc of radius at 55 m. The threshold range at the 30°-from-axis limit is 51.3 m. By repeating the profile on either side of the central profile, one increases the efficiency, which translates to the requirement for a pulse energy of 1.5 μJ. Taking reflection losses into account, this results in a need for 1.9 μJ per pulse from the laser.
Testing the units
Engineers tested both of the simulation systems by positioning the optical aperture over the center of a motorized rotary table. A lens with an aperture in its focal plane focuses the output beam onto a detector. Rotational data from the table and output of the detector are sent to a data logger to allow recording the intensity profile of the unit as it rotates.
Meet the author
David Page is R&D manager at Precision-Optical Engineering in Hitchin, UK.