Broadband quantum light sources with many frequency modes in a single waveguide show potential for scalable quantum state generation.
MICHAEL KUES, CHRISTIAN REIMER, PIOTR ROZTOCKI, DAVID MOSS AND ROBERTO MORANDOTTI, INSTITUT NATIONAL DE LA RECHERCHE SCIENTIFIQUE (INRS)
Quantum mechanics offers a range of properties that have a great potential for complex information processing capable of outperforming classical processes. As commercial quantum cryptography and even quantum computing have been realized in recent years, research into on-chip quantum light sources has emerged as a broad and promising field, driven toward the development of a practical and powerful platform that will bring quantum information systems out of the lab.
Photons, in particular, are well-suited to carry quantum information. In comparison to solid-state quantum systems based on the agglomeration of atoms, ions or electrons that need extensive and complex shielding from both thermal and electromagnetic environmental noise and necessitate operation at cryogenic temperatures, photons interact very little with their surrounding environment. Therefore, they have longer de-coherence times — the average time until a quantum state is destroyed. Furthermore, photons can be prepared to form entangled states, which are photons with linked particle states that show unique, nonclassical correlations. These entangled states constitute the basis for quantum information processing, where entanglement can be achieved in various degrees of freedom, such as spatial modes, polarization, position, orbital momentum, frequency or time.
Complex photon states with entanglement shared among several modes are especially necessary for solving high-level problems in quantum information processing, quantum imaging and microscopy, as well as quantum communications. However, realizations of on-chip quantum states and manipulation gates have mainly focused on the use of polarization, or path-entangled photons, wherein each state dimension corresponds to a single waveguide mode. Such architectures run into scalability issues as both the quantum circuit footprint and intricacy scale with problem complexity, posing significant challenges for today’s fabrication technologies.
Recent research from a team from the Institut National de la Recherche Scientifique (INRS) illustrates how the concept of integrated frequency combs — broadband light sources comprised of equidistantly spaced spectral lines, with many frequency modes in a single waveguide — can bring about scalable, single-spatial-mode quantum state generation. By exploiting the resonance characteristics and nonlinear frequency-conversion effects of on-chip optical microring resonators, the team succeeded in the realization of a so-called “quantum frequency comb” — a multifrequency-mode quantum light source emitting correlated photon pairs, as well as bi- and multiphoton-entangled quantum bits (qubits, the quantum analogue of a classical bit) on many frequency modes, with direct applications for quantum communications and computation. The approach is compatible with contemporary fiber network infrastructure and with chip-scale semiconductor technology, enabling compact, low-cost and scalable implementations.
Nonlinear microring resonator
At the basis of realizing large, complex photon states is the generation of correlated photon pairs: two photons that are created at the same instance and thus show correlations in their generation time.
The INRS approach toward an integrated multimode photon pair source is based on a nonlinear microring resonator (Figure 1) coupled to two access waveguides (four-port configuration). Similar to a free-space Fabry-Pérot cavity, consisting of two facing mirrors, the microring allows electromagnetic fields with only certain frequencies to resonate, propagate and to experience field enhancement inside the device. This characteristic is reflected in its transmission spectrum consisting of sharp spectral lines or resonances, which, for this device, are nearly perfectly aligned to the standardized 200-GHz-spaced telecommunications frequency grid. The microring resonator is based on a CMOS-compatible, high refractive index glass platform, featured by negligible nonlinear optical losses and a high effective nonlinearity. Thus, the resonant frequency components experience light-matter interaction while oscillating within the device, giving rise to nonlinear frequency conversion effects boosted by the field enhancement. A dominant effect is spontaneous four-wave mixing (SFWM), a third-order nonlinear process where two photons from an excitation field (or multiple fields) are annihilated, giving rise to the generation of two twin photons, referred to as signal and idler (Figure 1b). The effective dispersion is designed to be small and anomalous, guaranteeing a large four-wave mixing gain bandwidth at telecom wavelengths.
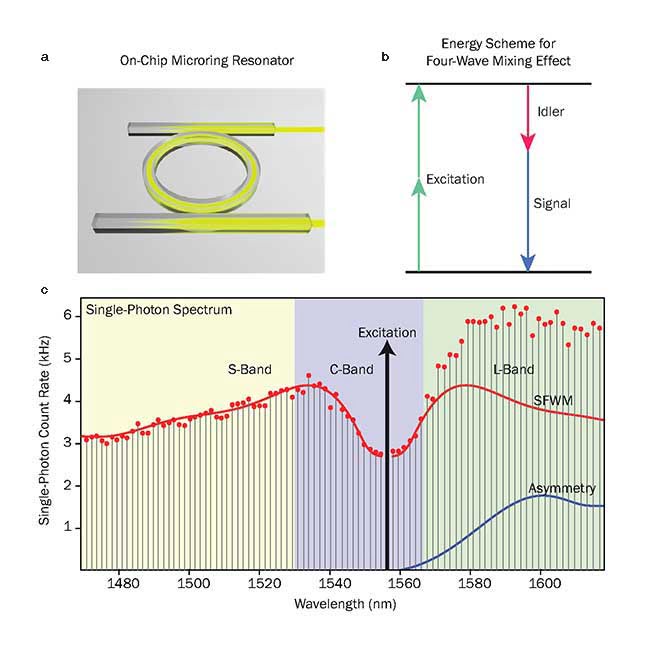
Figure 1. Schematic of four-port nonlinear microring resonator (a). Four-wave mixing effect (b). Single-photon spectrum emitted by the microring resonator when exciting a single resonance (c).
In order to exploit the four-wave mixing effect for the generation of photon pairs, the ring resonator needs to be excited by a classical laser field with a frequency matched to a resonance of the cavity. To avoid the use of an external pump laser (which leads to meta-stable pump configurations due to thermal and environmental changes and thus requires active stabilization), the team utilized a novel excitation scheme termed self-locked pumping. This scheme consists of embedding the microring in an external active cavity, including an erbium-doped fiber amplifier. Such a setup allows a continuous wave excitation of the ring resonator that is intrinsically locked to the resonance, rendering external stabilization unnecessary.
Correlated photons with narrow photon bandwidth
Excited by such a continuous wave field, the SFWM effect generates signal/idler photon pairs on each resonance symmetric to the excitation frequency. To measure their generation, the signal/idler pairs were separated from the classical pump field and then individually rerouted by a filter to single-photon detectors. The single-photon spectrum emitted by the microring resonator (Figure 1c) covers the S, C and L telecommunications band with more than 50 frequency pairs.
Since the signal/idler photons are generated in a single quantum process, the photons are correlated in their generation time, which is reflected in a coincidence peak in the correlation function of their arrival times. The measurement of the signal-idler correlation function for the first resonance pair around the excitation frequency is shown in Figure 2a. The full width half maximum of the coincidence peak of ~2.9 ns corresponds to 110 MHz, which is consistent with the linewidth of the microring resonator (140 MHz). This very narrow photon bandwidth is suitable for use with state-of-the-art quantum memories and quantum repeaters. Similar and clear photon coincidences were measured for all channel pair combinations of the first five resonances symmetric to the pump field, while no coincidences were measured between nondiagonal elements of the frequency matrix (Figure 2b), due to energy conservation.
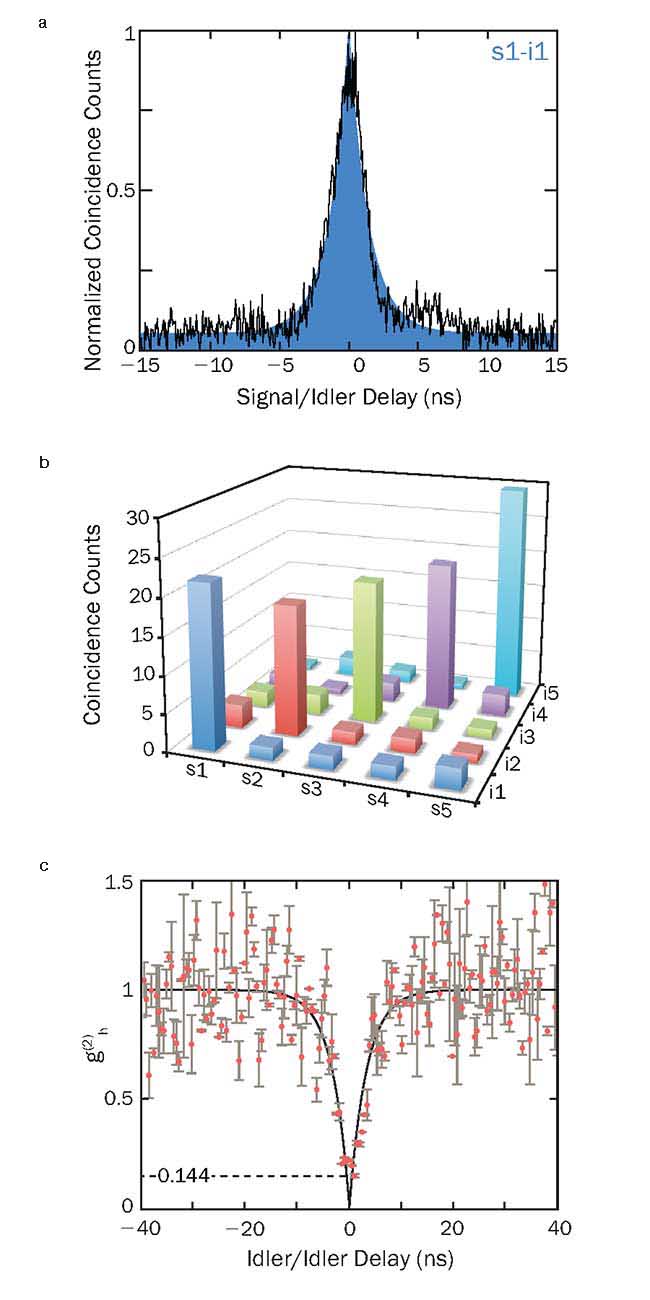
Figure 2. Correlation measurement of the first signal/idler pair (a). Correlation matrix showing all signal/idler channel combinations of the first five resonances (b). Heralded idler autocorrelation demonstrating the heralded single photon nature of the source (c).
Photon-pair sources based on nonlinear processes can be used as single-photon sources. Specifically, for the realization of so-called heralded single-photon sources, we can exploit the fact that the twin photons are created at the same time: One photon’s detection heralds the presence
of the other. In order to demonstrate a heralded single-photon source such that detection of a signal photon implies that precisely one idler photon is present, it is necessary to perform an idler autocorrelation that is heralded by the signal photon. For a true twin photon source, only a single photon is present in the idler arm, and thus no coincidences are expected at zero time delay. The researchers performed this measurement for a particular signal/idler resonance pair and found a dip as low as 0.144 in the heralded idler-idler correlation function (Figure 2c), below the required 0.5. Remarkably, this characteristic is exhibited over the whole bandwidth of the quantum frequency comb.
Generating bi- and multiphoton-entangled quantum states
Complex photon states hold answers to fundamental questions in quantum physics and are the cornerstone of quantum communication and computation. In order to extend our configuration to enable the generation of entangled photons on multiple frequency modes, we employed time-bin entanglement, where the photons are entangled in two time modes. This has several intrinsic advantages, including being particularly suitable for information processing and transmission, since it is directly compatible with integrated devices, is robust with respect to polarization fluctuations and can be preserved even over long propagation distances in standard fiber networks.
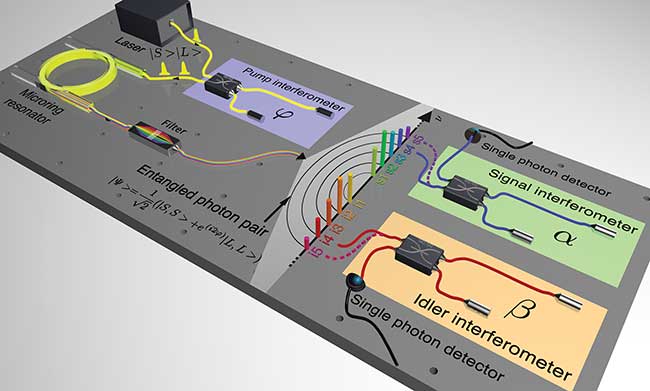
Figure 3. Experimental setup for the generation of a quantum frequency comb of time-bin-entangled photons.
The INRS team’s quantum frequency comb of entangled photons is generated using the previously described microring resonator. In this case, however, the device is pumped with a passively mode-locked fiber laser, which is spectrally filtered to excite a single ring resonance. This generated pure single-mode photons in each resonance, as confirmed by single-photon autocorrelation measurements. Starting from the single-mode photon pairs, the researchers generated time-bin-entangled qubits by passing the pulsed pump laser through a stabilized unbalanced fiber interferometer with a delay longer than the pulse duration of the laser, thereby producing double pulses of equal power with a definite relative phase difference. The double pulses were then coupled into the microring resonator. This pump configuration transforms the originally single-mode photon pairs into entangled states, where the two photons (signal, s, and idler, i) are in a superposition of two temporal modes, namely short |S? and long |L?. Most importantly, these entangled qubits are created over all the microring resonances, thus leading to a quantum frequency comb of time-bin-entangled photon pairs. In order to characterize the degree of entanglement, the generated signal and idler photons were each passed through a different fiber interferometer with an imbalance identical to the one used for the pump laser (Figure 3).
This setup allowed the measurement of quantum interference between the signal and idler photons. For five different frequency channel pairs within the C band, a quantum interference with raw visibility above 82.4 percent was recorded. Being greater than 1/√2≈71 percent, this confirmed entanglement through the violation of the Clauser-Horne-Shimony-Holt (Bell-like) inequality (Figure 4a).
Four-photon state
The distinct multimode characteristics of the frequency comb architecture presented here can be further exploited to create multiphoton-entangled states. By selecting two different signal-idler pairs (Figure 4a,b), it’s possible to generate two-photon qubit states. By post-selecting four-photon events with one photon on each frequency channel, the two states are multiplied, resulting in a four-photon time-bin-entangled product state.
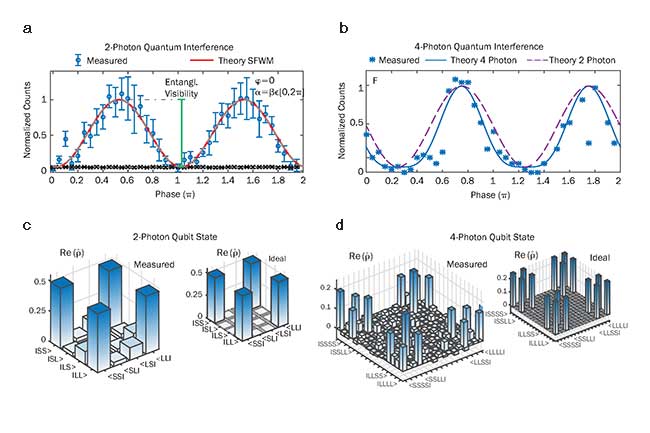
Figure 4. Quantum interference measurements for the 2-photon- (a) and 4-photon- (b) entangled state. Tomographic reconstruction of the density matrix for the 2-photon- (c) and 4-photon- (d) qubit state.
For the generation of a four-photon state, the coherence length of both photon pairs has to be the same and must be matched to the excitation field’s coherence time. This requirement is intrinsically fulfilled through the resonant characteristics (equal resonance bandwidths) of the ring cavity, in combination with the excitation scheme described above. The researchers performed four-photon quantum interference measurements (Figure 4c). Four-photon interference generally is not present for two completely independent two-photon qubit states. The data follow the expected relation, having a visibility of 89 percent without compensation for background noise or losses.

An illustration depicting the size of a next-generation optical chip.
To fully characterize the entangled states, the researchers performed
quantum state tomography. This analysis reconstructs the state’s density
matrix, from which it is possible to extract important characteristics
such as fidelity, which describes how close the measured state is to the
targeted entangled state. The team first measured the two-photon qubits
generated on comb lines that were symmetric with respect to the pump
wavelength (Figure 4b) and found a fidelity of 96 percent, confirming
that the generated quantum states are of high quality and very close to
the ideal entangled state. For the four-photon entangled state (Figure
4d), the researchers obtained a fidelity of 64 percent without
compensation for background noise or interferometer imperfections, a
value comparable to the fidelity measured for nonintegrated four-photon
states used for practical applications. The generated four-photon state
is the product of two Bell states and constitutes a good starting point
to create more complex states by manipulation through quantum gates or
the involvement of more resonance frequencies to achieve six, eight, or
more photon states.
The researchers’ results indicate that integrated quantum frequency comb sources based on third-order nonlinearities allow the generation of many frequency-mode quantum states in one spatial-waveguide mode and can open up new venues for the generation of complex quantum states, thus providing a scalable and practical platform for optical quantum information processing.
Meet the authors
Dr. Michael Kues is an early-career physicist who specializes in optics. His research focuses on exploring new physical concepts in integrated photonics systems for optical information processing; email: [email protected].
Christian Reimer is an early-career physicist who specializes in nonlinear optical phenomena in on-chip and nanostructured devices for both classical and quantum optical applications; email:[email protected].
Piotr Roztocki is a Ph.D. student at INRS-EMT, interested in applied and fundamental research in the fields of nonlinear, integrated and quantum optics; email: [email protected].
Professor David Moss has a 35-year career in research including seven years in industry. He is a Fellow of the IEEE and Optical Society of America; email: [email protected].
Roberto Morandotti is full professor at INRS-EMT in Montreal since 2008. He is a Fellow of the APS, OSA and RSC, among others; email: [email protected].