Majorana-like photons possess distinct properties of mixed-spin and orbital states, making them attractive for quantum computing and other applications.
SANDRA MAMANI AND ROBERT ALFANO, THE CITY COLLEGE OF THE CITY UNIVERSITY OF NEW YORK; LINGYAN SHI, THE UNIVERSITY OF CALIFORNIA, SAN DIEGO; AND DANIEL NOLAN, CORNING RESEARCH AND DEVELOPMENT CORP.
A special, newly proposed photon called a “Majorana-like” photon possesses spin angular momentum (SAM) and orbit angular momentum (OAM) coupled together. Experiments with mouse brain tissue have revealed the plausibility of using these special photons in imaging and communications applications, and possibly in optical quantum computing applications as the qubits of information. Not all photons are the same; they possess various salient properties.
Currently, there is an international challenge to build computers based on quantum mechanics instead of classical physics. In the U.S., corporate giants such as IBM and Google, and government labs such as NASA, are actively pursuing quantum computers. Quantum computers are based on the principles of entanglement and superposition, which offer the possibility of carrying a lot more information than a standard computer. These types of computers with great computational power will be capable of solving highly complex, big-data problems in seconds — problems that could take years or may even be unsolvable with a classical computer. Efforts to perform faster calculations at the quantum level are based on the use of superconducting circuits because the circuits exhibit low noise and decoherence of the Cooper pair excitations. These efforts, however, are too complex for everyday computers at room temperature. Quantum computers, which need to be in cold temperatures to reach computational stability, require a novel form — such as using photons — to implement quantum operations.
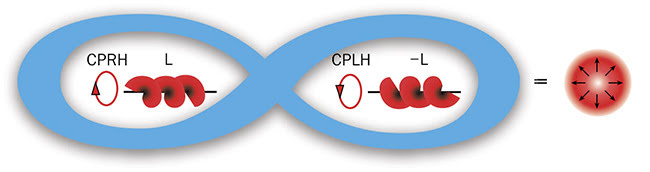
Figure 1. A representation of a radially polarized Majorana-like LG beam. A Majorana-like beam has its SAM and OAM (±L or ±l) entangled in a single particle. Bessel beams are not Majorana at z. CPRH: circular polarization right hand; CPLH: circular polarization left hand. Courtesy of Robert Alfano/The City College of New York News.
The photon is a fundamental quantum particle. The underlying basic principle of quantum mechanics is superposition of a wave function, which the photon can possess. The photon’s superposition principle is contained in Young’s classic double-slit experiment performed in 1801, with photons in the form of qubits, which have two basis states at once, while a triple-slit is based on qutrits — three basis states at once. Using n of these states gives a much larger number of bits of 2n and 3n states for higher-dimensional states — conserving the quantum feature of superposition.
Current classical computers, of course, rely on bits with a definite value of 0 or 1. Quantum computers rely on quantum bits, or qubits (combinations of 0s and 1s), which behave as if they have values of 0s and 1s simultaneously (until they are experimentally observed). This distinct trait is similar to that of Majorana-like photons. The use of n-coupled Majorana photons may form special photons entangled in spin and orbit to be implemented for superposition for quantum computers.
New frontier of optics
Majorana-like photons, unlike most
other photons, are an entangled mixture of polarization and wavefront chirality. The mixture is what makes these photons unique and suited to several applications.
In the past, researchers focused on optical computing, and there are now significant optical elements available to make up quantum logic gates (CNOT, or controlled-NOT gates), as well as memory devices. Memory devices are essential to building quantum computers and include polarizers, wave plates, spatial light modulators, optical fibers, mirrors, beamsplitters, filters, and photodiodes. Researchers are now pursuing various technologies that could be used as the qubit — the heart of the quantum computer — such as ion traps, nuclear magnetic resonance, and superconductor circuits. But these techniques are not useful in commonly used compact computers at room temperature. For common computers, photons offer advantages such as speed and salient properties that make them free of noise or decoherence, which are detrimental to quantum computing. Therefore, using photons — particularly Majorana photons — is the key to developing an optical approach.
As mentioned earlier, these photons possess SAM and OAM coupled together as an entangled state with two states at once. These photons, which have a vortex-like appearance, play an important role in our research on the photon propagating deeper in biomedia. A photon’s SAM refers to the polarization chirality (right and left circular polarization). OAM is associated with a beam’s helical chirality wavefront.
One type of beam that carries OAM and SAM is a Laguerre-Gaussian (LG) beam1, which is characterized by an azimuthal phase dependence of exp(ilφ), where φ is the azimuthal angle, and l dictates the times
a beam twists for its wavefront. The LG
optical beams can carry different types of polarization, including linear polarization (LP), left circular polarization (LCP), radial polarization (RP), and azimuthal (AZ) polarization. RP and AZ are vector vortex beams (VVBs) with an inhomogeneous wavefront of polarization structure and a nonseparability property.
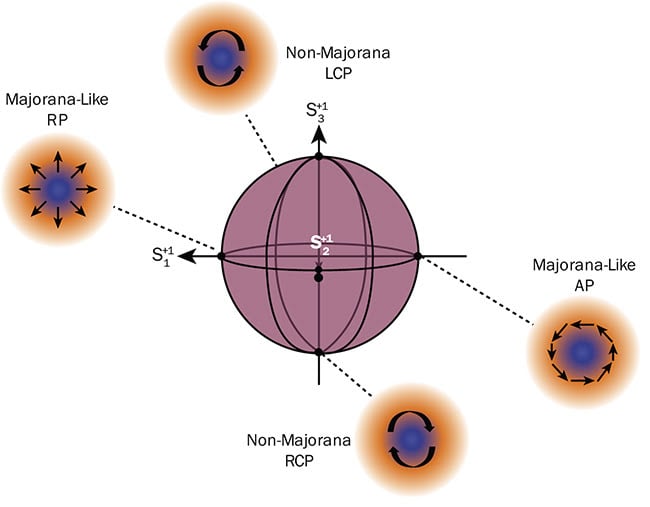
Figure 2. An illustration of the higher-order Poincaré sphere geometric representation of various states of polarizations classified as Majorana-like vector beams and non-Majorana beams. The poles represent the non-Majorana beams: The North Pole is represented by the left-hand circularly polarized beam, and the South Pole by the right-hand circularly polarized beam. The equators represent the Majorana-like VVB, radial and azimuthal. Courtesy of Sandra Mamani.
Some of these LG beams possess the fingerprint of a Majorana photon where the anti-conjugate wave function feature is its antiparticle ψ = ψ*. Our research reported Majorana VVBs and non-Majorana-like beams propagating through a mouse brain tissue for examining the transmission of SAM-OAM and polarization2.
In the recently published work, a new classification is proposed for VVBs, named Majorana-like vector photon beams2 for
imaging. These are special Majorana-like boson particles named after the Italian theoretical physicist Ettore Majorana3. These special photons possess novel salient properties, among which are combined chirality of polarization (SAM) and
structure (OAM), giving the beam a vortex-
like characteristic at once.
Remarkably, the SAM and OAM can be
coupled in a single photon package, which makes it a special photon. These beams can be the basis of qubit for optical quantum computers; of course, this can be viewed as a highly speculative statement.
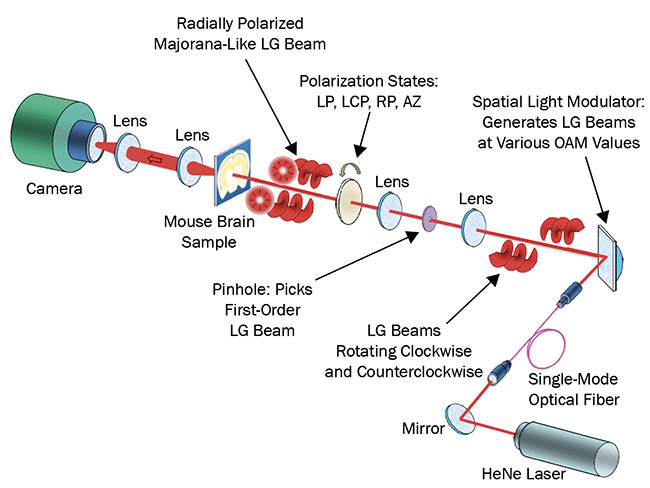
Figure 3. An experimental setup for transmission using Majorana-like VVBs and non-Majorana photons. Courtesy of Journal of Biophotonics.
A Majorana-like photon as defined here consists of a mixed state at once, having a mixture of both right- and left-handed polarizations and both +L and −L OAM. Two very notable examples of Majorana-like photons are the radial and azimuthal Laguerre-Gaussian optical beams. These two Majorana-like vector beams are mainly characterized by their nonseparable nature of polarization and OAM, which refers to its polarization and space orbital wavefront degree of freedom. In this key paper in 20192, it was shown mathematically that these two types of special photons are their own anti-photons, hence, named Majorana-like vector photons (Figure 1). We propose here that these special Majorana-like photons can act like quasiparticles and can be the basic qubit for optical quantum computers. In addition, these two types of Majorana-like vector photons are neutral and massless, which are other features of Majorana-like particles.
‘Majorana-like’ photons possess spin angular
momentum (SAM) and orbit angular momentum (OAM) coupled together.
In 1932 and 1937, Ettore Majorana proposed that particles could be composed of both fermions and bosons together as particles and antiparticles3,4. Electrically neutral particles can indeed be their own antiparticles such as the photon, following the key Majorana state characteristic of ψ = ψ* (the wave function is equal to its complex conjugate). Taking the complex conjugate of a VVB, such as a radially polarized LG beam field (Equation 1) and an azimuthally polarized LG beam field (Equation 2), we obtain the following (see Equations 1 and 2).
Notice above, the Majorana is a mixture of states. Hence, the result will be itself (anti-photon) because both VVBs are in a superposition of both SAM and ±OAM (spin-orbit entangled state).
The key property of a Hermitian state function can be shown in Equations 1 and 2. Hence, both types of VVBs are Majorana-like bosons. However, when taking the complex conjugate of right or left circularly polarized states, it shows to be non-Majorana-like, the same for linear polarization with l ≠ 0. Figure 2 depicts the Majorana and non-Majorana-like beam on a higher-order Poincaré sphere (HOPS)5. This is a geometric representation of various polarization states of an optical vortex beam. The Poincaré sphere and HOPS offer ways to implement
photon quantum states. These spheres are made up of three Stokes parameters (S1, S2, S3), which are used as the Cartesian coordinates. This sphere is specifically representing the l = 1, making the final coordinates: S (l, 1), S (l, 2), and S (l, 3).
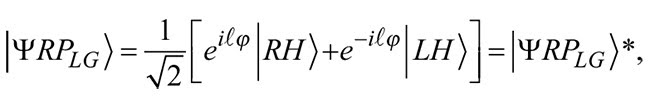
Equation 1
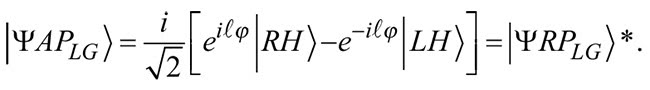
Equation 2
Experimentally2, Majorana-like VVB and non-Majorana LG beams propagating through a mouse brain are depicted in Figure 3. This brain tissue acts as a highly scattering chiral media6. In this experiment, two brain tissues with thicknesses of 120 and 600 µm, respectively, were investigated at various polarizations and odd OAM values (l = 0 − 7). The beam penetrated into the most important regions that are mainly affected by neurodegenerative diseases such as Alzheimer’s. The overall transmission for RP and AZ (Majorana-
like) was high; this was attributed to their nonseparability property and dual-chirality nature. A prominent effect of higher OAM values was observed with LCP,
attributed to its pure state. LP showed almost a nonsignificant effect. Figure 4 shows two of the more prominent results obtained for Majorana and non-Majorana-like vortex beams’ transmission in mouse brain tissue.
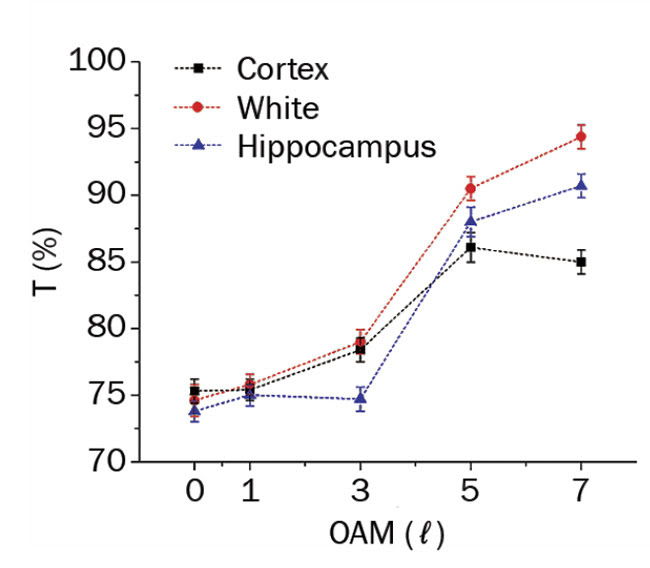
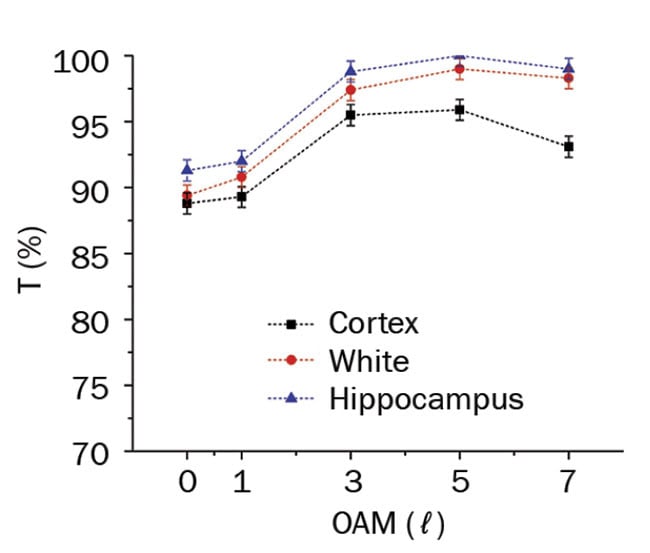
Figure 4. Transmission as a function of OAM for left circularly (top) and radially (bottom) polarized states. These graphs show that the radially Majorana-like vector beam has a more transparent transmission, while the LCP non-Majorana shows less transmission, but a stronger dependence of OAM. Courtesy of Journal of Biophotonics.
In conclusion, Majorana-like photons arise from a class of vector vortex beams, following ψ = ψ*, which showed potential improvements in transmission in scattering and nonlinear optical media. The Majorana-like VVBs could be an advantage when propagating through a turbid media because its properties could remain almost the same regardless of the scattering and turbulence. This beam is locally entangled and offers a basis for nonlocal correlations, which will be a challenge
to generate. Majorana-like propagation can be useful in a variety of fields, such
as neuroscience, imaging, quantum or classical communication, optical quantum computing, free-space, turbulence, nonlinear optics, and fiber propagation, where coherence is a challenge due to environmental noise or highly dense turbid media. The HOPS sphere5,7 may be used for quantum computing algorithms with structured Majorana-like photons as qubits in optical devices and quantum computers, where photons should be at the heart.
Acknowledgments
We thank the partial support of Corning Research and ARO (473510001). We thank Larry Jacobowitz and Pouyan Ghaemi for discussions.
Meet the authors
Sandra Mamani is a doctoral student in electrical engineering at the Grove School of Engineering at The City College of New York (CCNY) of the City University of New York (CUNY), and a researcher at the Institute for Ultrafast Spectroscopy and Lasers. Her main area of research includes the generation and use of OAM and SAM beams for optical
imaging and nonlinear optics.
Robert Alfano is distinguished professor of science and engineering at CCNY of CUNY. He discovered the supercontinuum. His research has led to advancements in ultrafast laser science, biomedical optics, and nonlinear optical imaging.
Lingyan Shi is assistant professor in the bioengineering department at the University of California, San Diego. Her primary research interests focus on developing and applying novel linear and nonlinear optical techniques for studying neuroscience, cancer, and metabolism.
Daniel Nolan, Ph.D., is a corporate fellow
at Corning Research and Development Corp.,
working on fiber optics, quantum optics, optical science, and complex light.
References
1. L. Allen et al. (1992). Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A, Vol. 45, 8185.
2. S. Mamani et al (2019). Majorana vortex photons a form of entangled photons propagation through brain tissue. J Biophotonics, Vol. 12, e201900036.
3. J. Magueijo (2009). A Brilliant Darkness. New York, N.Y.: Perseus Book Group.
4. F. Tamburini et al. (Feb. 17, 2018). Majorana states for subluminal structured photons. arXiv, 1707.07160v4.
5. G. Milione et al. (2011). Higher-order Poincaré sphere, stokes parameter, and the angular momentum of light. Physics Rev Lett, Vol. 107, 053601.
6. M. Zamorano and H. Torres-Silva (2006). FDTD chiral brain tissue model for specific absorption rate determination under radiation from mobile phones at 900 and 1800 MHz. Phys Med Biol, Vol 51, 1661.
7. G. Milione et al. (2012). Higher-order Pancharatnam-Berry phase and the angular momentum of light. Phys Rev Lett, Vol. 108, 19040.