
Structured Photons Open Door to High-Dimensional Quantum Gates
Encoding quantum information into the spatial properties of single photons shows great promise for increasing information capacity per photon.
By Marcus Huber, Markus Hiekkamäki, and Robert Fickler
Quantum communication offers
unparalleled security and is arguably the most advanced application of quantum information science. Its fundamental strength derives from the fact that single photons can transmit information. While all observation and measurement induce some level of back action, this back action can be safely neglected in the classical world.
Observing a car requires light to shine on it, but the momentum transferred by the photons is negligible when compared to the momentum of the car itself. For single photons, the impact of the measurement back action cannot be avoided without breaking the rules of quantum mechanics itself. Measuring the physical state of a single photon alters the state, and when two photons share the special quantum connection called entanglement, measurement of either photon will inevitably break it. Although this feature appears to be detrimental to communications, it can actually help with detecting eavesdroppers who are trying to hack the communication channel. Thus, the security of
quantum communication is not derived from mathematical assumptions, as in classical encryption, but from truly physical principles.
This advantage, which is unique to quantum communication, is also its greatest Achilles’ heel. During communications over longer distances or in noisy backgrounds, many of the single photons employed will be accidentally measured by the environment or simply lost along the way. With a few photons arriving at the target destination, when encoding information, it becomes even more important than in classical optics to use the full bandwidth of photons in order to counteract low bit rates.
And here lies the real challenge: Most quantum experiments have focused on polarization as the degree of freedom in which to encode information. But polarization is fundamentally limited to one of two distinguishable states — horizontal or vertical — leaving at most one bit per photon to be communicated. Although limited to so-called 2-level quantum bits, or qubits, polarization is still one of the most popular ways of encoding quantum information, due to a simple fact: It is easy to reversibly manipulate the polarization of single photons, without causing any disturbance, through standard elements used in linear optics.
The ability to perform such transformations is the basis for most quantum information tasks. The transformations are, of course, a prerequisite for processing quantum information and arguably the key enabling technology of quantum communication. However, in addition to polarization, other degrees of freedom of light can be used to encode quantum information. Photons have color, momentum, position, and arrival times1. While these other properties of photons can increase information capacity through so-called high-dimensional encoding — by using distinguishable states termed “qudits” — reversibly manipulating qudits is notoriously difficult.
One of the most prominent high-
dimensional encodings in everyday use is a QR (quick response) code. It is a spatial encoding that is easily recognized by mobile phones, and often encodes information by positioning black and white pixels on a two-dimensional plane (Figure 1). Depending on the number of pixels, a single QR code not only allows the storage of binary black or white information — such as a single pixel or bit — it enables the encoding of multiple bits that can store more complex information in a single structure.
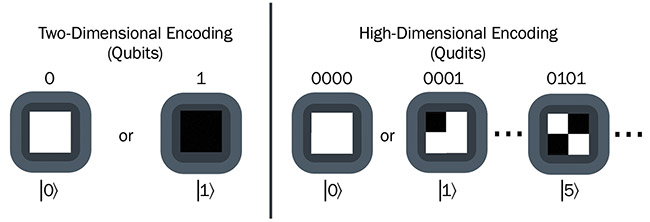
Figure 1. Carriers of two-dimensional bits can only have two values, such as 0/1 or black/white. In quantum information, such systems are called quantum bits or qubits and are commonly denoted by a bracket notation, such as |0 and |1
and |1 . Photons carrying qubits as quantum information only transmit a single bit of information (left). However, when encoding carriers in a high-dimensional-state space, it becomes possible to store multiple bits of information on a single carrier. Instead of just carrying black or white information of a single pixel, high-dimensional encoding essentially allows encoding of an entire QR (quick response) code into a single photon. A 16-dimensional example (right). Courtesy of Tampere University.
. Photons carrying qubits as quantum information only transmit a single bit of information (left). However, when encoding carriers in a high-dimensional-state space, it becomes possible to store multiple bits of information on a single carrier. Instead of just carrying black or white information of a single pixel, high-dimensional encoding essentially allows encoding of an entire QR (quick response) code into a single photon. A 16-dimensional example (right). Courtesy of Tampere University.
In principle, the same technique could be used to increase the capacity of quantum information imprinted on single photons. In other words, the technique could encode information in the spatial part of the quantum wave function of single photons. In fact, such complex encoding has already been achieved in pioneering experiments that show the possibility of high-dimensional entanglement wherein spatial structures of two photons are correlated in a uniquely quantum manner2.
However, to truly utilize these encodings and fully benefit from the enhanced information capacity in quantum information technologies, it is crucial to allow reversible transformations of one “spatial code” to another one, performed on single photons without disturbing them.
Transverse spatial modes
Such complex transformations of photonic structures, performed in the quantum regime, were recently achieved. Instead of using a QR code pattern for encoding quantum information, however, the experiment implemented complex transverse spatial structures — so-called transverse spatial modes — and, in particular, modes of the Laguerre-Gaussian family (Figure 2).
These spatial modes have attracted a lot of attention over the last 25 to 30 years due to the benefits that their manifold interesting properties offer to various fields of optics3. For example, the stable ring-like intensity structure (|0 or |1
or |1 in Figure 2) has enabled superresolution microscopy. The additional orbital angular momentum ascribed to some structures has been used to set particles in rotation using optical tweezers. The complex propagation dynamics have rendered studies of fundamental optics possible — such as self-accelerating beams or polarization knots. The availability of different modes as novel transmission channels has offered the possibility for multiplexing classical information in optical communication and other systems.
in Figure 2) has enabled superresolution microscopy. The additional orbital angular momentum ascribed to some structures has been used to set particles in rotation using optical tweezers. The complex propagation dynamics have rendered studies of fundamental optics possible — such as self-accelerating beams or polarization knots. The availability of different modes as novel transmission channels has offered the possibility for multiplexing classical information in optical communication and other systems.

Figure 2. The transverse-spatial structure of photons comprises one degree of freedom that can be used to encode high-dimensional quantum information. To effectively encode multiple bits of information, however, it is necessary to appropriately discretize the spatial domain. Instead of dividing the space into pixels, use of propagation-invariant spatial modes can form an infinite set of orthogonal structures. Because a single photon can be shaped into any of these structures, it can encode high-dimensional quantum information. These are examples of spatial modes from the Laguerre-Gaussian mode family (upper row, left) and a complex superposition of different Laguerre-Gaussian modes (right). All of these structures have spatially varying phase and intensity profiles that are visualized through a color map and by brightness, respectively. Courtesy of Tampere University.
In the quantum realm, these modes enabled, if not initiated, the experimental study of using high-dimensional qudits to boost the performance of quantum communication methods by making the methods more robust to noise and increasing the amount of distributed quantum information they can encode4.
But how do the benefits of these mode structures compare to the aforementioned encoding of pixels based on QR code patterns? The answer to this question is twofold. To begin, the maximum information capacity of such modes is larger than that of a QR code when comparing optical systems of the same size. The underlying reason is simple: The cylindrical symmetry of these modes perfectly matches most of the optical devices used for long-distance transmission of information, such as fibers or telescopes.
In addition, and maybe more importantly, transverse spatial modes are propagation invariant, meaning that the structure in which the information is encoded does not fade out and remains unchanged even if the photons are sent over large distances — apart from the unavoidable divergence natural to any light propagation. Hence, any information encoded using these stable spatial modes can be retrieved after the photon arrives at a receiver.
While a lot of research has sought the best technique to generate and detect photonic modes and study various transmission channels, the simple, efficient, and flexible transformation between multiple modes was shown experimentally only a few years ago. Its demonstration has been applied in optical communications when combining the signal of multiple single-mode fibers into a single optical beam with multiple modes5. The underlying method relies on multiple consecutive transverse phase modulations that adjust the wavefront of the transmitted light in a complex spatially varying way. While the modulation itself only alters the phase of the wavefront, the propagation between the modulations enables a lossless modulation of the light’s amplitude.
The transformation of beams from various fibers into a single beam of many modes allows the multiplexing of classical optical signals. However, the transformation that recent experiments have demonstrated is slightly more complex because the encoding of quantum information requires simultaneous transformation of multiple complex structures into multiple other complex structures, ideally without inducing any loss or disturbances caused by imperfections.
Figure 3 shows one example of an important transformation for quantum communication. Specifically, three input modes are transformed into complex
superpositions — specific coherent combinations of the three modes. Such a transformation is called the Hadamard gate in the language of quantum information, and it is required to measure the photon’s state in a complementary basis, which is a task that fundamentally ensures the security of quantum communication.
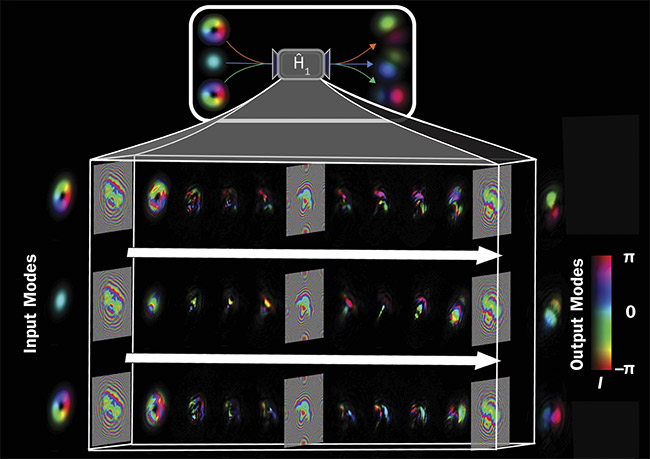
Figure 3. A unitary mode conversion achieved through multiplane light conversion. The unitary devices, performing such structure-dependent transformations, were constructed by placing multiple phase modulating elements one after another to achieve a continuous modulation of the spatial mode of a photon. In the device, various input modes undergo different transformations (shown in each row), which allows the transformations to be used as quantum gates (i.e., as operators that act on the quantum information carried by the single photons). Courtesy of Tampere University.
Putting theory into practice
While quantum information theory defines the transformations required for quantum communication, the challenging part is to design, implement, and test the modulations for real-world quantum systems — such as single-photon states — in the laboratory. Such designs were recently demonstrated using a wavefront matching technique that simulates the propagation of various light modes through a given number of modulation planes6. The simulation algorithm tries to consecutively match different input structures to desired output structures in the best possible way for each modulation plane and subsequent propagation. The structure of the photons that are sent through the modulations are then turned step by step into the desired output modes.
This means that, theoretically, an infinite number of modulations would enable an ideal transformation between an infinitely large set of modes. Of course, modulations often invoke losses that can lead to errors due to imperfect alignment. A crucial part of the research aimed to find the best trade-off between the number of modulations, the complexity of the transformation, and the ease of implementation7.
The experiments demonstrated that up to five different input modes can be flexibly modulated in nearly every possible manner. (See Figure 4 for the experimental setup and Figure 5 for a close-up of a spatial light modulator performing the light transformation.) The method enabled implementation of the Hadamard transformation for different numbers of modes and various mode combinations. Moreover, the experiments not only implemented some transformations for the first time, they also demonstrated transformations for which no other realizations are known.

Figure 4. The experimental setup shows the path and propagation direction (red arrows). The single photons are sent into the system from a single-mode fiber (bottom left), and a single spatial light modulator is used to imprint any arbitrary spatial mode onto the photons. The photons are then directed into the multiplane light conversion system (right). The system performs the spatial mode unitary by bouncing the photon between a single spatial light modulator and a mirror multiple times, each time on a slightly shifted lateral position, to enable multiple different consecutive modulations. Courtesy of Tampere University.

Figure 5. A close-up of the spatial light modulator as it performs the unitary transformation. The light path and structures are made visible with a laser and a long exposure time. Courtesy of Tampere University.
Some of the demonstrated modulations are known to be fundamental building blocks for quantum computing tasks, and could be implemented as quantum gates in a larger-scale, high-dimensional quantum computer. By applying spatial encoding, a gate that usually requires two quantum systems — a so-called controlled-NOT gate — can be created using a single system with two spatial degrees of freedom, here the azimuthal and radial domains. Using multiplane mode conversion and the spatial mode encoding, this complex quantum operation has been demonstrated for the first time in the laboratory. Although this method can bypass difficulties in getting two photons to interact, it has limitations when scaling to large computational tasks. Nevertheless, it shows that using spatial encoding has multiple benefits in areas other than quantum communication.
While the technique and the discussed demonstrations are promising first steps, many hurdles remain before similar modulations can be found in future quantum communication systems. The most pressing questions with respect to commercial quantum technologies are how to implement such transformations on a smaller scale and how to make the methods more efficient and stable. These questions will be explored in subsequent application-driven research. But the initial experiments have paved the way for novel fundamental studies. These include multiphoton interference methods along a single beamline using solely high-dimensional spatial modes, or the generation of special multiphoton quantum states that can increase the sensitivity of measurements beyond what is possible with classical optics.
Meet the authors
Marcus Huber leads a group working at the interface of theoretical and experimental physics at the Institute for Quantum Optics and Quantum Information (IQOQI) in Vienna. He also likes to look at beamsplitters; email: marcus.huber@univie.ac.at.
Markus Hiekkamäki is a doctoral researcher at Tampere University in Finland, working under the supervision of Robert Fickler. He studies structured light in the context of quantum photonics and quantum information science; email: markus.hiekkamaki@tuni.fi.
Robert Fickler is an assistant professor at Tampere University and an Academy Research Fellow of the Academy of Finland. He is working on quantum photonics and quantum information, with a focus on structured light; email: robert.fickler@tuni.fi.
References
1. M. Erhard et al. (June 25, 2020). Advances in high-dimensional quantum entanglement. Nat Rev Phys, pp. 1-17.
2. M. Krenn et al. (2014). Generation and confirmation of a (100 × 100)-dimensional entangled quantum system. Proc Natl Acad Sci, 111(17), pp. 6243-6247.
3. M.J. Padgett (2017). Orbital angular momentum 25 years on. Opt Express, Vol. 25,
No. 10, pp. 11265-11274.
4. S. Ecker et al. (2019). Overcoming noise in entanglement distribution. Phys Rev X,
Vol. 9, No. 4, p. 041042.
5. G. Labroille et al. (2014). Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt Express, Vol. 22, No. 13, pp. 15599-15607.
6. N.K. Fontaine et al. (2019). Laguerre-
Gaussian mode sorter. Nat Commun, Vol. 10,
No. 1, pp. 1-7.
7. F. Brandt et al. (2020). High-dimensional quantum gates using full-field spatial modes of photons. Optica, Vol. 7, Issue 2, pp.
98-107.
Published: September 2020