Rüdiger Paschotta, RP Photonics Consulting GmbH
With an increased quantitative understanding of the operation of Q-switched lasers come huge benefits for laser design. This first article in a two-part series focuses on actively Q-switched lasers; the second part covers passively Q-switched lasers.
Q-switched solid-state lasers have been used since the early 1960s, and their operation principles are theoretically well known. However, many working in the field do not sufficiently understand various details.
The basic idea behind Q-switching of a laser is to pump the laser gain medium for some time while preventing laser operation, and then to suddenly allow for laser operation, so that the stored energy is quickly released in the form of a short, intense light pulse. To control the laser emission, we introduce optical losses that are initially high and then suddenly lowered. In the case of active Q-switching, an electrically controlled modulator is used, normally an acousto-optic or electro-optic modulator.
Storing excitation energy
The pump phase should not last much longer than the upper-state lifetime of the gain medium – otherwise, much of the energy is lost via spontaneous emission. At high laser gains, amplified spontaneous emission may substantially increase the energy loss, but in bulk lasers this is usually not a concern. A more likely problem is parasitic lasing due to unwanted reflections or an unwanted Q-switch.
At high excitation levels, there may also be significant nonradiative processes. For example, neodymium-doped laser crystals such as Nd:YAG tend to lose a lot of energy when they are highly excited, particularly for high Nd concentrations. Therefore, it is not a good idea to use a much higher Nd concentration than is a requirement for efficient pump absorption.
The power losses introduced by the modulator must be high enough in the pump phase to prevent any lasing. With an acousto-optical modulator (AOM) in the usual zero-order configuration, the sound-induced diffraction of light must be strong enough to suppress premature lasing, while the switched-off AOM in the lasing phase naturally causes only small losses.
An important parameter of the laser crystal is its saturation fluence (Fsat = hv/σem), with the laser photon energy hv and the emission cross section σem (assuming a four-level laser medium). Multiplied with the pump beam area A, this gives us the saturation energy Esat. The single-pass exponential laser gain coefficient is then simply obtained as g = Es/Esat with the stored energy Es. For example, if we wanted to store 10 mJ in Nd:YAG (Fsat = 0.67 J/cm2) with a beam radius of only 100 µm, that would result in g = 48, corresponding to 4.343 × 48 dB = 208 dB, which is far too much. A more appropriate beam radius would be 1 mm, resulting in a manageable 2.1 dB of gain. We need to store the 10 mJ within 200 µs, for example, so for diode pumping at 808 nm, we will need a pump power of the order of (1064/808) × 10 mJ/200 µs = 66 W, plus an addition for spontaneous emission – say, 100 W.
Pulse buildup
Now we consider the pulse buildup. The initial round-trip gain in decibels will be two times the single-pass gain (assuming a linear resonator) minus the loss at the output coupler and the (normally smaller) parasitic losses at the AOM, for example. Taking the above example with 30 percent output coupling (1.5 dB), we have an initial round-trip net gain of ≈2.5 dB, which means a bit less than doubling the power within one round-trip time of 1 ns. Once the gain is fully exhausted by saturation, the net losses of ≈1.5 dB will lead to a somewhat slower decay of output power.
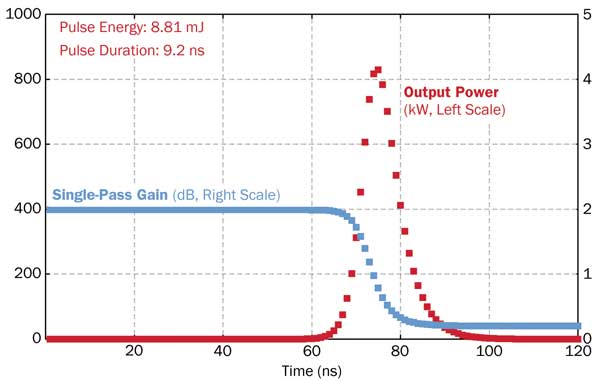
Figure 1. Evolution of output power and gain in a Q-switched laser, simulated for top-hat pump and signal profiles.
In a first numerical simulation, we assume simple top-hat beam profiles with a 1-mm radius for pump and signal, no parasitic losses and an ideally efficient Nd:YAG crystal 20 mm long with 0.15 percent Nd concentration. With 100-W pumping over 200 µs, we get 9.8 mJ stored and 2-dB gain. Figure 1 shows the temporal evolution of output power and gain. In a 9.2-ns pulse, 8.8 mJ can be extracted.
Influence of beam profiles
A more realistic simulation assumes Gaussian profiles for pump and signal beam (Figure 2). Here we get somewhat less output power, essentially because the power extraction is less efficient in the wings of the beam profile. The initial neodymium excitation reaches up to 23 percent, which is quite substantial – it should not go much higher.
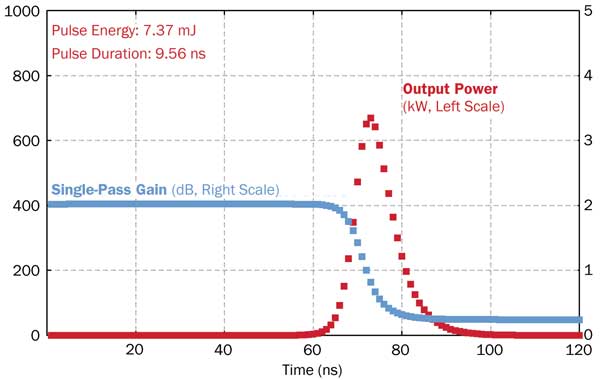
Figure 2. Same as Figure 1, but more realistic with Gaussian beam profiles. The energy extraction is somewhat less efficient.
For the simulation, we have implicitly assumed that the beam shape remains constant during pulse evolution, although the significant laser gain causes some gain guiding effect: The on-axis radiation is substantially more amplified than the wings of the beam profile. More refined simulations based on numerical beam propagation can be used to investigate such effects, which also depend on the laser resonator design.
Resonator design issues for high pulse energies
Many Q-switched solid-state lasers have a fairly simple laser resonator with only two mirrors: a flat output coupler and a curved, highly reflecting mirror on the opposite side, through which the pump power can be injected (Figure 3). It may seem easy to apply this to our example laser: Just use a very large curvature radius of −100 m for the curved mirror to obtain a beam radius near 1 mm for a resonator length of 126 mm, as required for a 1-ns round-trip time.

Figure 3. A simple resonator of a Q-switched laser. The laser crystal can be end-pumped through the right mirror.
However, even a reduced pump power of 10 W (e.g., for a 100-W pump source with 10 percent duty cycle) causes a thermal lens of roughly 0.2 diopters, and this would already shrink the beam to a radius ≈0.5 mm. We can compensate for that thermal lens with a convex (defocusing) end mirror with a curvature radius of +5.3 m (instead of the original −100 m).
We can try this out with a numerical beam-propagation simulation. Figure 4 shows that, although it basically works, gain guiding initially makes the laser beam substantially smaller than the resonator mode as calculated without beam guiding. Once the gain is saturated, the beam gets substantially larger. This behavior also has a somewhat detrimental effect on the beam quality. Fine-tweaking of the parameters could improve the performance, but it remains sensitive to small changes of thermal lensing, pump beam shape and alignment. For example, a lateral shift of the pump beam profile by only 0.1 mm (10 percent of the beam radius) reduces the pulse energy by about one-third.
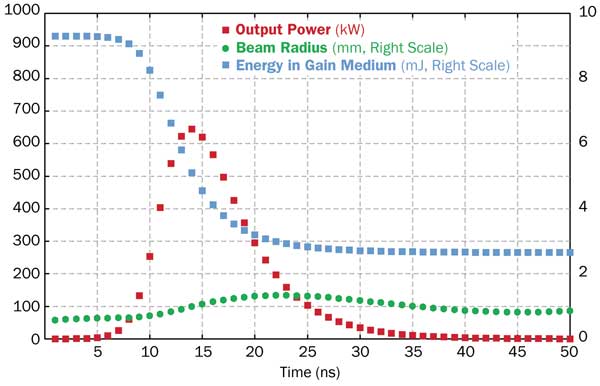
Figure 4. Temporal evolution of output power, stored energy and beam radius during pulse generation, simulated with numerical beam propagation. The model is based on the software RP Fiber Power.
Various issues arise when designing lasers for high pulse energies. To limit the gain, we need a large pumped area. If the beam quality should be high, this implies a large resonator-mode area. At the same time, the resonator should usually be short to obtain short pulses. The problem with this regime is essentially that divergence effects become very weak – the beam profile is stabilized by a balance of weak divergence, weak (de)focusing and significant gain guiding; it also becomes sensitive to misalignments. A possible remedy is to use a telescope inside the resonator, leading to a smaller mode in part of the resonator – this may, however, raise the risk of mirror damage. Another solution can be to use a so-called unstable resonator design with a variable reflectivity mirror, such as one with a Gaussian reflection profile.
It can also be advantageous to use a gain medium with higher saturation fluence and accordingly smaller mode area. Nd:YLF for 1047-nm or particularly for 1053-nm emission offers some improvement. Nd-doped glasses have even lower cross sections; however, they also have much poorer thermal properties.
Lasers with high pulse repetition rate
Many Q-switched lasers are operated in a different regime: with high pulse repetition rates of 10 kHz, 100 kHz or even more. The energy per pulse and the stored energy before each pulse are then substantially lower. As a result, we can design a laser with smaller mode areas, avoiding or mitigating the problems mentioned above.
For very high repetition rates, the actual challenge may be to obtain a sufficiently high laser gain despite the small stored energy (low gain implies longer pulses and potentially less efficient energy extraction). This can be an issue even for high average powers, because these may demand larger beam areas. In that regime, a laser crystal with lower saturation energy (higher emission cross section), thus providing a higher laser gain, is preferable. Nd:YVO4 is a popular choice. Its lower upper-state lifetime is not a problem, as the high emission cross section keeps the laser threshold quite low.
Better than trial and error
These examples show that some simple analytical guidelines already provide a reasonable understanding of basic design parameters of a Q-switched laser, whereas working based on unfounded guesses could easily lead to problematic regimes concerning laser gain, stored energy, extraction efficiency and excitation levels. At minimum, a pure trial-and-error approach would be very inefficient.
Numerical simulations with realistic beam profiles and possibly with numerical beam propagation still give more accurate predictions. They allow us to reliably check the impact of certain potentially detrimental effects such as a mismatch
of mode sizes, gain guiding and misalignment, or low switching speed of the modulator. This helps us find optimized designs efficiently and avoid wasting time and money with failed attempts.
Meet the author
Dr. Rüdiger Paschotta is the founder and managing director of RP Photonics Consulting GmbH in Bad Dürrheim, Germany; email: [email protected]. He also developed the RP Fiber Power software as used for all numerical simulations in this article.