Digital imaging requires a re-examination of the resolution limits of optical microscopy.
Sripad Ram, Dr. E. Sally Ward and Dr. Raimund J. Ober
Optical microscopy is an important tool for
studying live biological cells in life sciences research, enabling the observation
of various biological processes in real time. The study of nanoscale single molecular
activities such as protein-protein interactions is vital for understanding cellular
processes and aids in the development of new drugs. Recent advances in imaging technology
and labeling methodology have enabled the study of single biomolecules even within
a cellular environment.
It is widely believed that optical microscopes
have a finite resolution limit given by Rayleigh’s criterion. This limitation
has long been held as an impediment to studying nanoscale molecular interactions.
However, it is well-known that the criterion is based on heuristic notions.
Formulated within a deterministic framework
at a time when the unaided human eye was typically used as the detector, Rayleigh’s
criterion neglects the statistics of the detected photons and does not take into
account the total number of them. Therefore, it is not suited for current microscopy
techniques that use highly sensitive photon-counting detectors. Not surprisingly,
recent single-molecule experiments have shown that Rayleigh’s criterion can
be surpassed.1,2 Thus, its inadequacy necessitates a reassessment of the resolution
limits for optical microscopes.
In particular, to properly plan an
experiment, it is important to have a methodology to assess the accuracy at which
the distance between two point sources can be determined. Recently, a resolution
measure that overcomes the limitations of Rayleigh’s criterion was proposed.
It predicts that the resolution of an optical microscope is not limited and that
it can be improved by increasing the number of detected photons from the point sources.
Single-molecule imaging experiments have verified that distances between single
molecules that are well below Rayleigh’s criterion can be measured with an
accuracy in accordance with that prediction.3
The resolution measure
According to optical diffraction theory, the image
of an in-focus point source is described by an intensity distribution profile; i.e.,
the point-spread function. In fluorescence microscopy, the image of two point sources
can be described as the sum of two point-spread functions. Rayleigh’s criterion
is based on the spatial overlap between two point-spread functions. The minimum
resolvable distance between two point sources is given by 0.61 λ/na,
where λ denotes the wavelength of the photons and na denotes the numerical
aperture of the objective lens.
The resolution limit specified by Rayleigh’s
criterion can be thought of as an attempt to quantify the distance between two point
sources such that their presence can be visually distinguished in their image. That
is, point sources that are spaced far apart are resolvable because their image contains
two well-separated peaks, each of which corresponds to a point-spread function,
whose presence can be visually identified in the image by a human observer. As the
distance of separation between the point sources decreases, there is significant
overlap between the two point-spread functions such that the presence of two peaks
can no longer be visually identifiable in the image (Figure 1). In this case, the
point sources are said to be unresolvable.
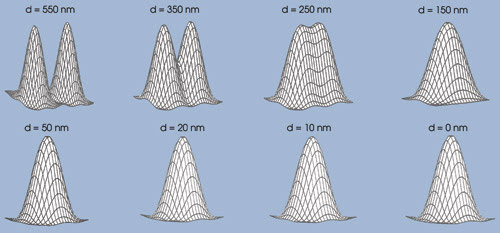
Figure 1. These simulations show GFP single molecules imaged at different
distances (d) of separation. Rayleigh’s resolution limit for the GFP molecules
is ~ 220 nm.
However, the image of two point sources
is distinct from that of a single point source because, mathematically, the sum
of two point-spread functions is different from that of a single point-spread function.
Although this was known even during Lord Rayleigh’s time, it was not taken
into consideration, possibly because of the insensitivity of the unaided human
eye to detect subtle shape changes.
With the advent of digital technology,
images can be captured easily by a digital imaging sensor and analyzed with appropriate
computer algorithms. This, in turn, means that distances well below Rayleigh’s
resolution limit can be resolved in data acquired in an optical microscope setup.
Photon statistics play a crucial role because collecting a large number of photons
(i.e., data points) from the two point sources provides more information about the
shape of their image, which leads to higher accuracy in determining the distance
between them.
Fundamental resolution measure
An interdisciplinary approach was used to obtain
the new resolution measure in which tools of advanced statistical image processing4
address a classical problem in optical microscopy. The task of determining the distance
between two point sources is a parameter-estimation problem. By using the theory
concerning the Fisher information matrix, a bound/limit is obtained to the accuracy
with which the distance can be estimated for a given imaging condition. An analytical
expression for the fundamental resolution measure (FREM) is obtained by assuming
imaging conditions analogous to those of Rayleigh’s criterion — i.e.,
two identical, self-luminous, in-focus point sources emitting unpolarized, incoherent
light.
The FREM predicts how accurately the
distance between two point sources can be resolved. A small numerical value of the
FREM predicts a high accuracy in determining the distance, while a large numerical
value predicts poor accuracy.
For example, consider a pair of GFP
molecules that are imaged by a 1.45-NA objective. According to Rayleigh’s
criterion, distances of 8, 50 and 200 nm between the GFP molecules cannot be resolved
because the smallest resolvable distance is about 220 nm. On the other hand, the
new measure predicts that these distances can be resolved with accuracy not smaller
than ±6.4, ±2.7 and ±1.9 nm, respectively, when 3000 photons, on
average, are detected from each molecule. This implies that, for distances of 50
and 200 nm, the FREM predicts a high accuracy in resolving the distance, while for
8 nm, it predicts poor accuracy in resolving the distance (Figure 2A).
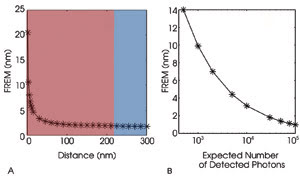
Figure 2. The FREM results vary depending
upon distance (A) and photon count (B) for a pair of GFP molecules. For a given
photon count, the FREM deteriorates with decreasing distances of separation because
its numerical value becomes larger as the distance of separation between two point
sources becomes smaller (A). Because of the inverse square root dependence of the
FREM on photon count, this deterioration can be offset by collecting more photons
from the point sources (B). For comparison purposes, Rayleigh’s criterion
is shown graphically in A, where the red and blue regions denote distances that
are irresolvable and resolvable, respectively, and the corresponding Rayleigh’s
resolution limit is ~220 nm. Reprinted with permission of PNAS.
Because the FREM takes into account
the photon statistics, the accuracy of resolving a distance of 8 nm can be greatly
improved by increasing the number of photons detected from each GFP molecule (Figure
2B). This result is in stark contrast to Rayleigh’s criterion, which is independent
of the photon count. Moreover, it underscores the importance of considering the
photon/light budget when discussing resolution performance, especially in fluorescence
imaging applications that typically use photobleachable fluorescent markers.
Several experimental factors can affect
the resolvability of two point sources. For instance, modern imaging detectors are
pixelated, and the data acquired is a discretized version of the image. The data
also is corrupted by extraneous noise sources such as scattered photons, autofluorescence
and detector readout noise. To account for these factors, the practical resolution
measure (PREM) was derived. An extension to the FREM, it shows how experimental
factors deteriorate the predicted resolution measure.
For example, for a pair of GFP molecules,
a comparison of the PREM and the FREM shows that, when taking into account deteriorating
factors, there is an approximately twofold deterioration in the resolution measure
for distances of 50 and 200 nm and a sevenfold deterioration for a distance of 8
nm. Note that the deterioration of the resolution measure is pronounced
for small distances. This implies that, during an experiment in which small distances
are estimated, extra care must be taken to control noise. Moreover, by comparing
the PREM and the FREM, an experimenter also can systematically investigate which
experimental factor is a major contributor to the deterioration of the predicted
accuracy in a particular scenario. In this way, the new resolution measure also
can be used to design and optimize microscopy and experimental setups.
The FREM and PREM are based on the
scenario that the acquired image contains photons from both point sources. However,
when the point-source pair exhibits double-step photobleaching behavior, additional
spatial information can be obtained from photons collected from the point source
that remain after the first photobleaching step. The theory used to derive the FREM
and the PREM also can be used to investigate how the additional spatial information
improves the predicted resolution measure.
For example, for two GFP molecules
10 nm apart, the resolution measure predicts an accuracy not better than ±5.8
nm when an average of 5000 photons are collected before and after the first photobleaching
step. In contrast, when additional information obtained after the first
photobleaching step is not used, the resolution measure predicts an accuracy not
smaller than ±43 nm to resolve the same distance.
By definition, the resolution measure
provides a bound to the accuracy/standard-deviation with which the distance between
two point sources can be estimated. Hence, it is important to know whether this
bound can be attained in experimental data. To verify this, images of closely spaced
Cy5 molecules and a DNA ruler labeled with Cy5 dye at either end were acquired and
analyzed. To determine the distance of separation between the single molecules,
the maximum likelihood estimation algorithm was implemented in the high-level programming
language Matlab from MathWorks in Natick, Mass., and it was verified that the accuracy
of the distance estimates comes close to the predicted resolution measure.
Single-molecule imaging
The proposed resolution measure shows that certain
single-molecule experiments can be performed that were once thought to be unfeasible
with an optical microscope; for example, nanoscale protein interactions such as
receptor-dimerization. For this, the protein of interest is tagged with a single
fluorophore such as GFP. In addition, the analysis can be extended to resolve distances
between more than two single molecules.
Parameter estimation problems play
a central role in single-molecule microscopy. Examples include determining the location
and photon count of single molecules, resolving the distance of separation between
two (or possibly more) molecules and estimating the level of defocus. With all these
problems, it is helpful for the experimenter to have analytical tools to assess
with what accuracy the various parameters can be estimated.
In the past, several groups have addressed
this issue by considering specific estimation techniques, but the results have been
limited to the specific estimation technique used. On the other hand, the approach
based on the Fisher information matrix provides results independent of specific
estimation techniques. In fact, by using this approach, a simple analytical formula
provides a fundamental limit to the accuracy with which the location of a single
molecule can be determined.5
Results also have been obtained for
the problem of determining the defocus of the single molecule.6 In general, this
method can be applied to any parameter estimation problem in optical microscopy,
and a detailed formulation in this regard was recently reported.7
Meet the authors
Sripad Ram is a PhD student in the Joint Biomedical
Engineering graduate program at the University of Texas at Arlington/University
of Texas Southwestern Medical Center in Dallas.
Dr. E. Sally Ward holds the Paul and
Betty Meek — FINA professorship in molecular immunology and is with the Center
for Immunology at Southwestern Medical Center.
Dr. Raimund J. Ober is a professor
in the department of electrical engineering at the University of Texas at Dallas
and is an adjunct professor at the Center for Immunology; e-mail: [email protected].
References
1. M.P. Gordon, T. Ha and P.R. Selvin (April 27,
2004). Single molecule high resolution photobleaching. PNAS, pp. 6462-6465.
2. K.A. Lidke et al (Sept. 5 2005).
Super-resolution by localization of quantum dots using blinking statistics. OPTICS
EXPRESS, pp. 7052-7062.
3. S. Ram, E.S. Ward and R.J. Ober
(March 22, 2006). Resolution beyond Rayleigh’s criterion: a new resolution
measure with applications to single molecule microscopy. PNAS, pp. 4457-4462.
4. D.L. Snyder and M.I. Miller (1991).
Random point processes in time and space. Second edition. Springer Verlag, New York.
5. R.J. Ober, S. Ram and E.S. Ward.
(February 2004). Localization accuracy in single molecule microscopy. BIOPHYSICAL
JOURNAL, pp. 1185-1200.
6. S. Ram, E.S. Ward and R.J. Ober
(January 2005). How accurately can a single molecule be localized when imaged through
an optical microscope? Proc. of the SPIE, Vol. 5699, pp. 426-435.
7. S. Ram, E.S. Ward and R.J. Ober.
(January 2006). A stochastic analysis of the performance limits of optical microscopes.
MULTIDIMENSIONAL SYSTEMS AND SIGNAL PROCESSING, pp. 27-57.