A new concept enabling the realization of smaller resonators that exhibit higher performance opens the possibility of improved and novel applications.
Jacob Scheuer, William M.J. Green and Amnon Yariv,
California Institute of Technology
Circular resonators are key ingredients in the realization of many basic components for advanced optical communications systems. During the past decade, their application in numerous circular-resonator-based components such as lasers, filters,1 add/drop multiplexers,2 modulators3 and delay lines4,5 has been suggested and demonstrated. In addition, the applicability of circular resonators has been shown to extend beyond telecommunication to the fields of sensing,6 spectroscopy and standardization,7 as well as to basic research in quantum electrodynamics, nonlinear optics and other related fields.8
In a conventional circular resonator, light is confined in the guiding channel by means of total internal reflection (Figure 1). Similar to the principle of an optical fiber, the refractive index of the guiding channel is higher than that of the surrounding material, thereby confining the light. Because of the cyclic boundary conditions, the field in the resonator must satisfy a phase condition that discretizes the wavelengths that can resonate in the cavity: λm /n = 2ΠR/m, where n is the effective index, R is the ring radius and m is an integer. The discrete set of wavelengths λm is designated as the resonance wavelengths.
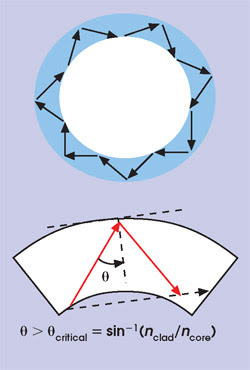
Figure 1. In a conventional circular resonator, total internal reflection confines the light inside the resonator. Light must be incident on the interface at an angle larger than the critical angle (θcritical ) for total internal reflection to occur. However, it is truly “total” only if the interface is flat, so some bending loss is inherent with the curved interfaces of the circular resonator.
Although both fiber optics and conventional circular resonators employ the same confinement method, they differ as a result of the bending of the waveguides in the resonators. Total internal reflection completely reflects the incident wave only when the interfaces are straight. If, as in a circular resonator, the interfaces are bent, the reflection is incomplete, and part of the light in the guiding channel leaks to the cladding, which results in a constant power loss from the waveguide.
This loss mechanism, often called bending loss, is inherent to the curved waveguide geometry. Bending losses depend primarily on the refractive index contrast between the core and the cladding and on the bending radius, wherein a lower index contrast and a smaller bending radius result in larger losses.
For many applications, the circular resonator is required to exhibit low losses or, equivalently, a high quality factor, or Q. Besides high Q, it is often desirable that the resonator have small dimensions — or, to be more precise, that it exhibit small modal volume. Unfortunately, these requirements are contradictory for conventional resonators, which utilize total internal reflection as the radial confinement mechanism. To exhibit small modal volume, a circular resonator must have a short circumference and a small bending radius. Under these conditions, the efficiency of the total internal reflection confinement mechanism is significantly impaired, leading to larger power dissipation and a lower Q.9
For a given bending radius, the radial confinement — and, hence, the bending losses — can be improved by increasing the index contrast between the core and the cladding. On the other hand, this increases the scattering loss resulting from surface roughness, which is proportional to the index contrast squared. Because there is a limit to the refractive index value of available optically transparent materials, the total internal reflection confinement mechanism inherently limits the ability to fabricate circular resonators with both low losses and small modal volumes. Decoupling between cavity dimensions and cavity losses requires an alternative confinement mechanism, such as distributed Bragg reflection.
Structure and design
Distributed Bragg reflectors are widely used in a variety of applications and devices, both in active ones, such as lasers, and in passive ones, such as filters and mirrors. The majority of distributed Bragg reflector structures employed in optical devices consist of periodic dielectric structures. This is because of the Bloch theorem, which indicates that structures with periodic variation of the refractive index can serve as efficient reflectors.10
Unlike total internal reflection, the Bragg reflection mechanism is not limited by the index contrast of the structure and the incident angle of the electromagnetic field, or the “critical angle,” because the periodic structure can be tailored to efficiently reflect any electromagnetic wave. In an ideal distributed Bragg reflector, the constituent layers are one-quarter-wavelength thick; i.e., di = λ/4ni, where ni is the refractive index of the ith layer. Such a structure ensures that the partial reflections from the interfaces separating successive layers accumulate identical phase (up to an integer multiple of 2Π) and, hence, interfere constructively, yielding high reflectivity.
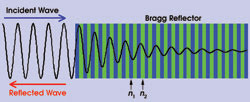
Figure 2. In a distributed Bragg reflector, the index interfaces are located at the zeros and the extrema (minima and maxima) of the field.
In a conventional distributed Bragg reflector, the corresponding field is a superposition of forward- and backward-propagating waves, or a standing wave (Figure 2). The amplitude of the field decreases exponentially in the reflector region because the power is efficiently transferred from the forward-propagating wave to the backward-propagating one; that is, the incoming wave is reflected. Because the layers forming the reflector are a quarter-wavelength thick, their interfaces are located at the zeros and extrema of the field profile. It has been shown that positioning the interfaces of the layers at the zeros and extrema of the field ensures an exponential decrease or increase in the field amplitude, depending upon which type of interface (high-index → low-index or low-index → high-index) is positioned at the zeros.11
Realizing an efficient Bragg reflector in the radial geometry, however, is not as simple as in the cartesian. There is no equivalent to the Bloch theorem indicating the index profile required for efficient reflection. Nevertheless, the structure of a conventional distributed Bragg reflector offers a good idea of how to construct a radial one: The interfaces of the Bragg structure should be positioned at the zeros and extrema of the field.
Without knowledge of the field profile (or, to be more precise, the phase of the field profile), a piecewise calculation is required. For each constant-index section (Bragg layer), the first step is to calculate the spatial distribution of the field. The second is to determine the appropriate width of that section so that its edge lies at an extremum or a null.
There is a close relationship and much similarity between the structures of conventional and radial distributed Bragg reflectors. In both cases, the layers of the distributed reflector are a quarter wavelength thick — if we relate the notion of “quarter wavelength” to the distance between a zero and the next extremum of the field. In a cartesian distributed Bragg reflector, this distance is constant for a given index of refraction because the solution of the wave equation is periodic; i.e., sine and cosine. But in the radial geometry, because the solutions (Hankel or Bessel functions) are not periodic, the widths of the Bragg layers vary according to the oscillations of a Bessel/Hankel function.12,13
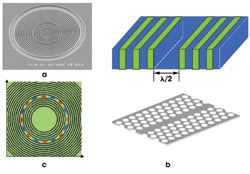
Figure 3. Radial and conventional distributed Bragg reflector structures are based on the same principle of Bragg reflection. A scanning electron micrograph reveals the structure of an annular Bragg resonator (a). The structure is a counterpart of Bragg and photonic crystal defect waveguides in the cartesian geometry (b). The modal field profile of an annular Bragg resonator illustrates the propagation of electromagnetic waves along the circumference of the defect (c).
Such a device, designated an annular Bragg resonator, features a ring resonator using radial Bragg reflectors on both sides of a radial defect (Figure 3a). The structure is the counterpart of a Bragg or photonic crystal defect waveguide in the cartesian geometry (Figure 3b). The widths of the Bragg layers and the guiding channel — also known as the “defect” — of the ring resonator are carefully engineered to support the electromagnetic waves propagating along the circumference of the defect while radially confining them in it (Figure 3c).
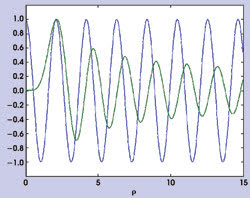
Figure 4. Both the amplitude and period of the cylindrical waves (Hankel functions in green) diminish with distance, while the amplitude and period of cartesian waves (sinusoidal in blue) are constant.
The guidance mechanism of the electromagnetic wave in the defect is similar to that of a cartesian Bragg/photonic crystal waveguide. In an annular Bragg resonator, however, the forward- and backward-propagating waves are replaced by radially outgoing and incoming cylindrical waves, represented by the Hankel functions of the first and second kinds. The amplitude of the cylindrical waves decays according to 1/p, while that of the cartesian wave remains constant (Figure 4). Moreover, the period of the cylindrical wave becomes smaller for larger radii, while the cartesian wave exhibits a constant period. The latter point, which involves the phase of the cylindrical wave, is the more important because it determines the structure of the appropriate Bragg reflector.
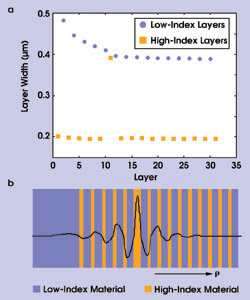
Figure 5. A nonperiodic distribution of high- and low-index materials is required in an annular Bragg resonator. The graph plots layer width versus radius (a), and the diagram depicts the radial field profile (b). The refractive indices of the high- and low-index materials are 2.0 and 1.0, respectively. In this example, light is confined in the high-index material, but other designs can confine light in the low-index material.
Figure 5 shows the widths of the Bragg layers as a function of the layer number and the corresponding field profile of an annular Bragg resonator. The high-index layers are not as wide as the low-index ones, and the width of both declines exponentially as a function of the radius, converging asymptotically to a constant value. The first property also exists in conventional distributed Bragg reflectors, and it stems from the dependence of the spatial oscillation period, or the “wavelength,” on the index of refraction. The second is unique to the cylindrical geometry and arises from the nonperiodic nature of the solutions of the wave equation (Bessel or Hankel functions) in this geometry.
At large radii, the widths of the Bragg layers converge asymptotically to the conventional quarter-wavelength condition. Mathematically, this can be explained by noting that, for large radii, the Bessel function can be approximated by a sinusoidal function divided by the square root of the radius. From the physical point of view, the curvature of the Bragg layers is small at large radii, and, therefore, the structure of a radial reflector structure is similar to that of a cartesian one.
The radial field profile of the annular Bragg resonator structure shows that the field is confined within the defect and that it decays while oscillating in the Bragg region. Although the overall envelope of the radial modal profile (averaging over the oscillations) is similar to that of a conventional ring resonator, the oscillatory behavior of the field in the reflector regions is the fingerprint of the distributed feedback mechanism.
Advantages and applications
Understanding the advantages of an annular Bragg resonator over a conventional one typically requires a consideration of specific applications. However, resonators exhibiting low loss and small dimensions are desirable regardless of the application.
The Bragg confinement mechanism affords great flexibility in engineering the radial field profile; for example, it becomes possible to design a resonator in which a defect composed of low-refractive-index material, or even air, confines the light — a configuration that is useful for sensing applications. This would not be feasible using conventional resonators based on total internal reflection. The finite difference time domain simulation of such a structure, referenced above and shown in Figure 3c, indicates that, although the defect consists of a lower-refractive-index material, the light is tightly confined within the guiding channel.
The Bragg reflection concept allows one to tailor the reflector structure to a desired radial field profile and to decouple between the modal volume (or cavity dimensions) and the radiation losses. In fact, radiation losses can be reduced almost arbitrarily simply by adding layers to the external Bragg reflector.
Another interesting and important property of the annular Bragg resonator structure is that it supports slow light propagation along the circumference of the defect. Because the Bragg reflector does not require the incident angle of the electromagnetic wave to be larger than some critical angle (as in devices based on total internal reflection), it is possible to design an annular Bragg resonator in which the incident angle of the wave is almost perpendicular to the Bragg layers. The angular component of the wave vector in such a case is very small and, thus, the angular propagation velocity is very low. This propagation mode has several advantages, including large gain (if the device is a laser), large and controllable dispersion and enhanced nonlinear response.
To demonstrate how these advantages reflect on specific applications, consider two examples: sensing and telecommunications. The most straightforward method of optically sensing the presence of an analyte is to detect the change it induces in the refractive index of its surroundings. Optical cavities are highly appropriate for this task because a change in the surroundings’ index of refraction will induce a shift in the resonance wavelength of the cavity. The larger the volume in which the electromagnetic wave interacts with the surrounding, the higher the sensor’s sensitivity.
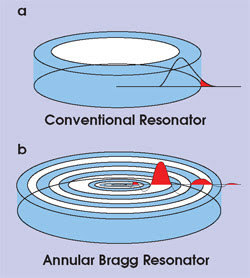
Figure 6. The electric-field profile of a conventional circular resonator (a) is significantly different from that of an annular Bragg resonator (b).
A comparison of the field profiles of a conventional ring resonator and of an annular Bragg resonator reveals that only the small evanescent tail of the field profile probes the surroundings in the former concept, while a much larger part of the field, including the main lobe, can interact with the analyte in the latter (Figure 6). This is especially true for an annular Bragg resonator incorporating an air defect because the main intensity lobe of the field is exposed to the surroundings.
The effect is apparent in a comparison of the shift in the resonance wavelength resulting from changes in the surrounding index of refraction for an annular Bragg resonator and for a conventional resonator of similar dimensions and materials (Figure 7). The sensitivity of the device is given by the slope of the curves; the sensitivity of the annular Bragg resonator is approximately 60 times higher than that of the conventional resonator.
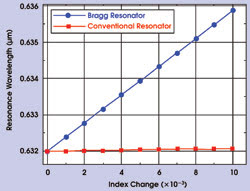
Figure 7. The sensitivity of an annular Bragg resonator to index change, indicated by the slope of the blue trace, can be 60 times that of a conventional circular resonator.
For resonator-based applications in telecommunications, low loss and small dimensions are always desirable. The strong dispersion characteristics of the annular Bragg resonator may be exploited to realize a compact dispersion compensator. Such application requires a coupling scheme into and out of the resonator. For example, the waveguides may be mounted either below or above the annular Bragg resonator — a vertical coupling scheme (Figure 8a).
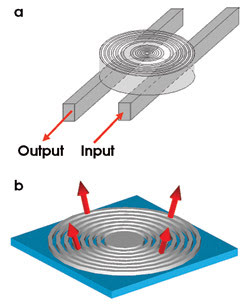
Figure 8. Light may be coupled into and out of a passive annular Bragg resonator using adjacent waveguides (a). A vertically emitting annular Bragg resonator laser may employ a second-order Bragg configuration (b).
Because of the low group velocity of the field in an annular Bragg resonator (i.e., the slow light discussed earlier), the achievable intensity inside the cavity is much higher than that inside conventional resonators with the same quality factor. This is because, for a given power level in the guiding channel, the corresponding field intensity is inversely proportional to the group velocity. An annular Bragg resonator thus can exhibit a strong nonlinear response even for relatively modest input power levels, and it may be used to realize integrated all-optical processing elements. Moreover, the low group velocity (as well as the high Q) may be exploited to attain very low threshold lasers.
For such an application, the annular Bragg resonator layer structure can be modified to efficiently emit light perpendicular to the surface, similar to a vertical-cavity surface-emitting laser (Figure 8b). This may involve the use of a second-order Bragg reflection scheme — a Bragg reflector consisting of three-quarter-wavelength layers.14 In such a reflector, the first Fourier harmonic of the structure reflects the incident wave in the vertical, out-of-plane direction, and the second Fourier harmonic is responsible for the in-plane reflection.
Fabrication and characterization
To examine the spectral and spatial properties of the optical modes supported by the annular Bragg resonator structure, we fabricated high-index-contrast radial Bragg gratings in active semiconductor material.15 The semiconductor medium consists of a 250-nm-thick InGaAsP layer (n ≈ 3.35 at λ = 1.55 μm) atop an InP substrate (Figure 9a). The InGaAsP layer includes six 75-Å-wide compressively strained InGaAsP quantum wells positioned at the center, with peak photoluminescence occurring at 1559 nm.
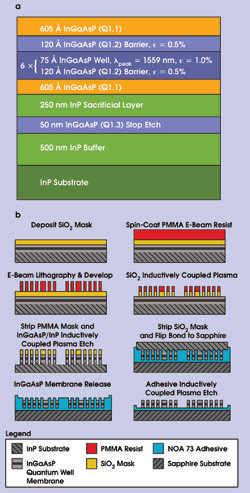
Figure 9. The epitaxial layer structure of the annular Bragg resonator laser includes six quantum wells (a). Fabrication of the laser is a multistep process (b).
The fabrication process involved several steps (Figure 9b). First, we deposited a SiO2 etch mask layer by plasma-enhanced chemical vapor deposition. Then, we applied a layer of PMMA electron-beam resist by spin-coating. The desired geometry was then defined using a direct electron-beam writer. After developing the resist, we transferred the PMMA patterns into the SiO2 etch mask layer by inductively coupled plasma reactive ion etching and removed the remaining PMMA with a gentle isotropic O2 plasma step.
The SiO2 layer served as a hard mask for pattern transfer into the active InGaAsP layer using an additional ion etch step. The patterns were etched to a depth of ~325 nm, completely penetrating the active membrane. Finally, we stripped the remaining SiO2 with a wet chemical etch. Figure 10 depicts scanning electron microscope images of devices at various stages of fabrication.

Figure 10. These scanning electron microscope images show an annular Bragg resonator in various stages of fabrication: a cross section of PMMA pattern after electron beam lithography and development, with the SiO2 mask layer visible between the PMMA and the substrate (a); an image taken after the SiO2 mask removal, with the radial defect as the sixth ring from the center (b); a magnified image of etched semiconductor grating, illustrating vertical and smooth sidewalls (c); and a magnified image of the semiconductor rings, taken after transfer of the membrane to the sapphire substrate and etching of the optical adhesive (d).
The near-field intensity pattern and the emitted spectrum of the annular Bragg resonators were examined at room temperature under pulsed optical pumping. Figure 11 depicts the experimental setup used to characterize the fabricated devices. The pump beam was focused on a sample with a 50× objective lens. The position of this lens controlled the size and the position of the pump spot. A 20× objective lens collected the vertical emission from the sample and focused it on an IR camera to obtain the near-field intensity pattern. A second lens coupled light into a multimode fiber, leading to an optical spectrum analyzer.
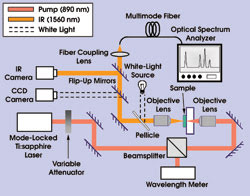
Figure 11. The annular Bragg resonator laser is pumped with a femtosecond Ti:sapphire laser. The red and orange beams represent the pump and resonator emission paths, respectively.
The resonators were pumped with a mode-locked Ti:sapphire laser emitting ~120-fs FWHM pulses at a repetition rate of 76.6 MHz, with a center wavelength of 890 nm. When the unpatterned quantum well layer structure was pumped, the emitted spectrum consisted of a wide peak centered at 1559 nm. When an annular Bragg resonator was pumped, the emission characteristics changed significantly.
Although the specific characteristics varied from device to device, all of the devices exhibited similar overall behavior. Once the pump intensity exceeded a certain threshold, clear and narrow emission lines appeared in the spectrum. As the pump intensity increased, the intensity of the emission lines increased as well, while broadening toward the shorter wavelengths.
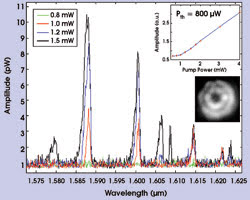
Figure 12. The emission spectra show a clear threshold between 0.8 and 1.0 mW. The light input/output curve also shows a threshold (upper inset). The near-field laser emission pattern is a pair of concentric rings (lower inset).
Figure 12 depicts the emitted spectra from an annular Bragg resonator for various pumping levels. The device consisted of a half-wavelength-wide defect surrounded by five and 10 reflection grating periods on the inner and outer sides, respectively. The upper inset of the figure shows a light input/output curve of the device, indicating a lasing threshold at 800 μW. Other devices exhibited even lower threshold levels, with the lowest being 600 μW.
The lower inset depicts the near-field lasing pattern of the annular Bragg resonator obtained at the maximum pump power. The pattern consists of two concentric rings of light, with the outer one localized within the defect. Finite-difference-time-domain simulations of the laser indicated that the effective index associated with this pattern is lower than the refractive index of the low-index material filling the gaps — an optical adhesive with a refractive index of ~1.54 — thus proving that the emitted pattern was confined by Bragg reflection.
References
1. C.K. Madsen and J.H. Zhao (1999). Optical Filter Design and Analysis: A Signal Processing Approach. Wiley Interscience.
2. B.E. Little et al (October 1988). Second-order filtering and sensing with partically coupled traveling waves in a single resonator. Opt. Lett., pp. 1570-1572.
3. A. Yariv (April 2002). Critical coupling and its control in optical waveguide-ring resonator systems. IEEE Photonics. Tech. Lett., pp. 483-485.
4. J.E. Heebner and R.W. Boyd (2002). “Slow” and “fast” light in resonator-coupled waveguides. J. MOD. Opt., pp. 2629-2636.
5. A. Melloni et al (March 2003). Linear and nonlinear pulse propagation in coupled resonator slow-wave optical structures. Opt. Quant. Electron., pp. 365-379.
6. C.Y. Chao and L.J. Guo (Aug. 25, 2003). Biochemical sensors based on polymer microrings with sharp asymmetrical resonance. Appl. Phys. Lett., pp. 1527-1529.
7. A.B. Matsko et al (2003). Whispering gallery mode based optoelectronic microwave oscillator. J. Mod. Opt., pp. 2523-2542.
8. K.J. Vahala (Aug. 14, 2003). Optical microcavities. Nature, pp. 839-846.
9. E.A.J. Marcatili (September 1969). Bends in optical dielectric guides. AT&T Tech. J., pp. 2103-2132.
10. A. Yariv and P. Yeh (1983). Optical Waves in Crystals: Propagation and Control of Laser Radiation. John Wiley & Sons Inc.
11. Ibid.
12. J. Scheuer and A. Yariv (November 2003). Annular Bragg defect mode resonators. J. Opt. Soc. Am. B., pp. 2285-2291.
13. J. Scheuer and A. Yariv (December 2003). Coupled-waves approach to the design and analysis of Bragg photonic crystal annular resonators. IEEE J. Quantum Elect., pp. 1555-1562.
14. J. Scheuer et al (November 2004). Low-threshold two-dimensional annular Bragg lasers. Opt. Lett., pp. 2641-2643.
15. W.M.J. Green et al (Oct. 25, 2004). Vertically emitting annular Bragg lasers using polymer epitaxial transfer. Appl. Phys. Lett., pp. 3669-3671.
Meet the authors
Jacob Scheuer is a research associate at the Center for the Physics of Information and in the department of applied physics at California Institute of Technology in Pasadena; e-mail: [email protected]. William M.J. Green is a graduate student in the institute’s department of electrical engineering; e-mail: [email protected]. Amnon Yariv is the Martin and Eileen Summerfield professor of applied physics and professor of electrical engineering at the institute; e-mail: [email protected].