Alexandre Y. Fong and Dr. Richard Young, Optronic Laboratories Inc., and Darren M. Haley and Brian K. Cromwell, Flir Systems Inc.
In the research and development and government test range communities, the need for calibrated, scientific-grade infrared cameras has grown because of demanding, leading-edge applications such as plume and missile target signature measurements and analyses. Such IR cameras generally operate in a relatively narrow band of the electromagnetic spectrum, typically 3 to 5 or 8 to 12 μm. The spectral response across these bands is usually not flat (Figure 1).
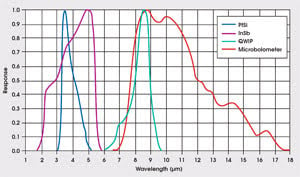
Figure 1. Typical IR camera detector materials exhibit spectral responses in the middle- and long-wavelength infrared band. PtSi = platinum silicide; InSb = indium antimonide; QWIP = quantum-well infrared photodetector.
Manufacturers can deliver IR cameras with radiometric or thermographic calibrations, but customers often opt for a noncalibrated system when it is to be used with exotic optics or custom filters or to be operated in what would be considered nonstandard integration times. This forces users to develop their own radiometric calibrations, which are often complex and unique to a given configuration of optical and sensing elements. To generate these calibrations, users must determine the total spectral responses of their camera for all configurations.
Methodology and theory
In basic terms, radiance detected by an IR camera is a combination of target radiance emission, target-reflected radiance, atmospheric transmission and atmospheric path radiance as measured through its total spectral response. Typically, the calibration of an IR camera assumes that a linear relationship exists between the radiance and counts detected for each specific temperature of a given blackbody source. Corrections must be made for target emissivity, atmospheric effects and the camera’s spectral response.
To calculate in-band radiance (L), an integral function can be derived that incorporates these terms. In this formula, L(λ,T) denotes spectral radiance at a given blackbody temperature; S(λ) signifies the spectral response of the camera; ε(λ) represents blackbody emissivity; and t(λ)a is the atmospheric transmission data usually generated by the modeling program ModTran, distributed by Ontar Corp. of North Andover, Mass.
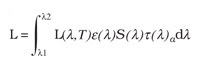
Using this equation with various blackbody temperatures and uniformity-corrected camera pixel values, off-the-shelf software, such as Flir Systems’ ThermaCam RTools, can generate a linear calibration equation for an IR camera. This equation can determine the radiance emitted from a target under test (denoted as LTarget). The coefficients K0 and K1 are the intercept and slope, respectively, and C is the analog-to-digital converter count value generated by the target scene at each pixel of the camera’s detector.
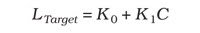
Measurement uncertainty
Users often make assumptions when generating IR camera calibrations. For example, one might assume that the camera lens transmits evenly across the band of interest. Also, one might assume that the focal plane array detector is spectrally flat or conforms to a “top hat” profile. Or, one might accept and use the nominal transmission data provided by vendors for their bandpass filters.
However, without accurate measurements of each of these elements, radiometric calibrations could have errors of 10 percent or more. This error estimate does not even account for effects from target spectral shape, atmospheric transmission and emissivity involved in thermographic measurements, among other factors.
For example, assuming that one has achieved a top-hat profile rather than using the actual, normalized spectral response of the camera introduces a level of uncertainty to radiometric calibrations (Figure 2).
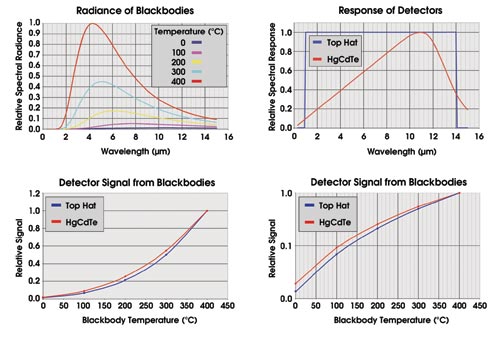
Figure 2. Assuming that one’s IR camera produces a top-hat response rather than using the actual, normalized spectral response can lead to significant calibration errors. The graphs show blackbody (Planck) curves at several temperatures (A); a top-hat response and a HgCdTe detector response (B); in-band energy generated from a blackbody as a function of temperature after being convolved with the previous top-hat and HgCdTe curves (C); and the energy differences that might be translated into measurement uncertainty (D).
Instrumentation and software
Commercially available radiometric software tool kits are widely used by government test ranges as well as by commercial researchers for data collection and analysis. Besides these functions, RTools can incorporate data from Optronic Laboratories Inc.’s OL series 750 spectroradiometric measurement system to automate the process of generating NIST-traceable calibrations of complex IR camera, filter and optics combinations.
With RTools used as a controller, the spectroradiometer can provide accurate, normalized spectral responses. A basic system, along with a selection of optional accessories, enables measurements over all or part of the middle- and long-wave IR region. An automated and computer-controlled trigrating mount, into which one can place up to three gratings, permits continuous scanning over extended wavelength ranges, and precision direct-drive wavelength positioning provides high-speed scanning under computer control. A fully automated second-order blocking filter wheel and automated slits allow selection of the system’s FWHM bandwidth.
A collimating optical attachment produces a uniform monochromatic beam from the spectroradiometer, and reference detectors with a known spectral response characterize the monochromatic energy across the spectrum of interest. The control software automatically steps the spectroradiometer through the desired wavelength range at the desired interval, while a frame grabber acquires data from the camera under test. After a complete spectral scan, the software generates a normalized spectral response of the camera. Transmission measurements of filters can be similarly performed.
Traceability
When radiometrically calibrating an IR camera, one should use a laboratory-measured spectral response to minimize measurement uncertainty. Convolving “typical” spectral responses provided by vendors of camera optical elements and sensors or assuming a top-hat camera response can lead to measurement uncertainty of 10 percent or more. Off-the-shelf hardware and software are available to automate the measurement of an IR camera’s spectral response. Given the highly variable characteristics of available focal plane array detectors, lenses and filters, one can obtain the most accurate response of any given configuration only by measuring the IR detector in combination with the other elements in the optical path. This method also offers traceability to support calibrations derived from a given setup.
To date, the response from the government range-testing community for this method has been extremely positive.
Meet the authors
Alexandre Y. Fong is vice president of marketing and sales, and Richard Young is vice president of science and technology, at Optronic Laboratories Inc. in Orlando, Fla.; e-mail: [email protected] or [email protected].
Darren M. Haley is manager of the science-grade camera program at Flir Systems — Indigo Operations in Goleta, Calif.; e-mail: [email protected]. Brian K. Cromwell is director of Indigo Advanced Systems in Niceville, Fla.; e-mail: [email protected].