Custom-designed fibers suppress nonlinearities and boost output power.
Donnell Walton, Corning Inc.
Fiber lasers are becoming increasingly popular alternatives for applications that require high power — hundreds of watts to kilowatts — such as materials processing, surgery and biochemistry. Their high efficiency, enviable beam quality, small footprint and low maintenance requirements make them ideal replacements for many other types of lasers that have dominated the marketplace in recent decades.
Although it seems counterintuitive that a tiny glass fiber, roughly the diameter of a human hair, could rival the output power of huge industrial lasers, the fiber’s small size is actually the secret of its success. The small diameter and long length — typically meters or tens of meters — provide an enormous surface-to-volume ratio, which in turn alleviates the greatest single obstacle to designing high-power lasers: removal of surplus heat.
But if the fiber’s small diameter — fiber cores are usually tens of microns or smaller — is key to its success, it also is a fundamental limitation. Because the core is small, optical power intensities are high, and because the fiber is long, these high intensities readily trigger nonlinear effects. The nonlinear effects, which couple laser light to other wavelengths and thereby limit power at the laser wavelength, are the prime limitation on the power available from fiber lasers today.
Stimulated Raman and stimulated Brillouin scattering are the two most prevalent nonlinearities in high-power fiber lasers. Stimulated Raman scattering is caused by the scattering of intense light from molecular vibrations in the glass host, and it can be effectively managed by reducing the intensity of light in the core. This can be accomplished through the use of large-mode-area fibers, where the core size is increased to decrease the intensity of the light it carries.
The drawback of this approach is that high-order modes can propagate in the larger cores, reducing the quality of the output beam. This can be at least partially compensated for by lowering the core’s refractive index, reducing its waveguide strength so that the highest-order modes are no longer guided. Further loss to high-order modes can be induced by bending the fiber, and all these effects together can lead to fiber lasers with good beam quality and stimulated Raman scattering thresholds on the 10-kW level. Nonetheless, there remains a desire to obtain high power operation in a truly single mode core to avoid the necessity of bending.
Our project team has designed a truly single mode fiber with a high stimulated Raman scattering threshold that operates at high power with a normal-size single-mode core. The high stimulated Raman scattering threshold was achieved with a fiber design that guides the laser wavelength but does not guide the longer (Stokes) wavelength created by stimulated Raman scattering. Thus, the fiber acts as a distributed filter for the Raman wavelength, greatly increasing the Raman threshold.
The fiber has two holes on either side of a central elliptical core (Figure 1). The holes lower the effective index of the core with respect to the cladding, thereby frustrating waveguide propagation at longer wavelengths. Meanwhile, the elliptical core induces a birefringence that distinguishes between the two polarization modes in the core.
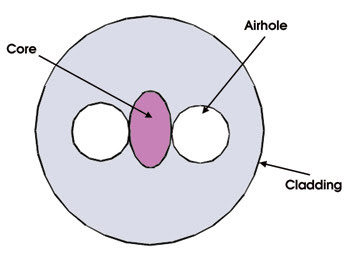
Figure 1. This dual-hole assisted, single-polarization fiber possesses a fundamental-mode cutoff that acts as a distributed spectral Raman filter.
Taken together, the holes and the elliptical core produce a polarization-dependent cutoff wavelength — the wavelength above which light is not guided in the core — for the fundamental mode. Thus, if we design the fiber so that the laser wavelength is between the two polarization cutoffs but the Stokes wavelength is beyond both, we obtain single-polarization, fundamental-mode propagation while filtering out the Stokes wavelength.
The other nonlinear effect, stimulated Brillouin scattering, is both more and less problematic than stimulated Raman scattering. It is less of a problem because it occurs only in lasers that have bandwidths less than a few tens of megahertz, but it is more of a problem in that, in a narrow-bandwidth laser, stimulated Brillouin scattering has a threshold two or three orders of magnitude lower than stimulated Raman scattering. Moreover, stimulated Brillouin scattering can be particularly dangerous because it scatters light backward toward the source, threatening to damage or destabilize it.
Stimulated Brillouin scattering results when the intense laser light in the fiber generates an acoustic wave via electrostriction — the compression of a material caused by an applied electric field. Laser light is then back-reflected (with a Doppler shift) from the index gradient of the acoustic wave. Stimulated Brillouin scattering can limit output powers in narrow-bandwidth lasers and amplifiers to a few hundred watts or less, even in large-mode-area fibers. It is clearly a problem that we must address if we want to achieve multikilowatt, narrow-bandwidth fiber lasers.
The stimulated Brillouin scattering effect can be analyzed through nonlinear wave equations that govern the evolution of the optical and acoustic fields in the fiber. This analysis shows that the threshold for stimulated Brillouin scattering obeys the relationship:
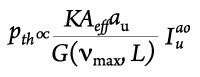
where K is the polarization factor, αu is the acoustic attenuation coefficient for the acoustic mode of order u, Aeff is the optical effective area, G(νmax, L) is the Brillouin gain at the peak frequency for a fiber of length L, and I is the normalized overlap integral between the electric and acoustic fields.
The equation indicates that the stimulated Brillouin scattering threshold can be increased by increasing the effective area, polarization factor and acoustic loss, or by decreasing the overlap integral and the maximum gain coefficient. Among all the factors that affect the stimulated Brillouin scattering, the effective area and the overlap integral can be controlled by tailoring the fiber’s optic and acoustic propagation indices.
Additionally, we can control the acoustic loss, αu, by modifying the glass composition. The Brillouin gain coefficient can be lowered by introducing along the fiber length a gradient of dopant concentration, temperature or stress. Furthermore, the interaction length between the acoustic and optic fields can be reduced by shortening the fiber, while increasing the dopant concentration to maintain the same laser gain.
We address stimulated Brillouin scattering by reducing the spatial overlap between the propagating optic and acoustic waves. The idea is that, just as various dopants can guide light in a fiber, we can likewise guide the acoustic field.
In an optical fiber, the core is doped with materials like germania and alumina to have a higher optical index than the cladding, so light is guided in the core. Analogously, dopants can be placed into the core and cladding regions to guide the acoustic wave. It turns out that, whereas alumina raises the index for the optical wave, it lowers that for the acoustic wave. Conversely, germania raises the index for both the optical and acoustic waves.
So, if we consider the standard germania-doped, step-index fiber, the indices for both the optical and acoustic fields are flat across the entire core region, with a sharp downward step at the cladding boundary. Thus, the fundamental optical and acoustic fields are similar throughout the core, resulting in a maximum overlap between the two.
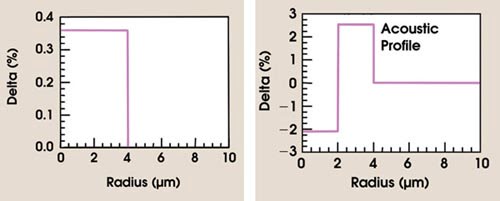
Figure 2. Altering the alumina and germania doping enables the optic and acoustic index profiles of the fiber to be tailored.
In contrast, suppose we dope the central region of the core with alumina and a circumscribing annular region of the core with germania (Figure 2). With the right concentrations, the optical field will have a homogeneously raised index across the core, whereas the acoustic field will have a germania-rich annular region with a raised index. In this case, the overlap between the optical and acoustic fields is reduced (Figure 3), and the stimulated Brillouin scattering threshold is significantly increased.
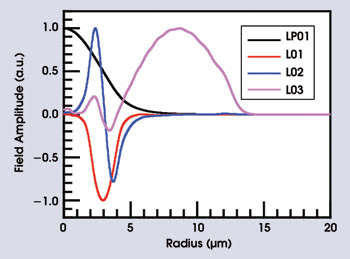
Figure 3. This plot shows the calculated intensities of the fundamental optical mode (LP01) and the three lowest-order acoustic modes of the fiber in Figure 2. The fundamental acoustic mode (L01) is confined to a germania-rich annular ring.
To validate our understanding, we fabricated a fiber with the dopant profile of Figure 2, and compared its stimulated Brillouin scattering threshold with that of standard step-index fiber with only germania doping. Both 12-m fibers had 30-μm-diameter cores, and both were doped with 0.5 percent ytterbium by weight.
To verify our special germania/alumina fiber’s acoustic profile, we measured the acoustic velocity across its preform with a scanning acoustic microscope. The result of this measurement indicates a high acoustic velocity (low acoustic index) in the center of the core and a low acoustic velocity (high acoustic index) guiding region at the edge of the core (Figure 4).
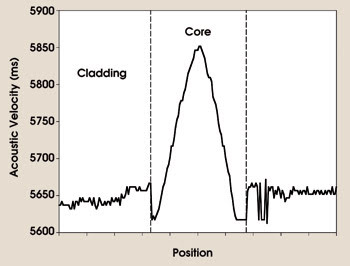
Figure 4. Surface acoustic micrograph data depict the acoustic velocity profile of the core and cladding regions of the fiber preform. A higher velocity indicates a lower acoustic index and vice versa. Thus, the highest acoustic index occurs at the outer edge of the core.
We measured the stimulated Brillouin scattering characteristics of the fibers by placing them, one at a time, in the second stage of a dual-amplifier, fiber oscillator-amplifier system. The oscillator generated narrowband (3 kHz), 150-mW input to the first amplifier at 1.064 μm. The first amplifier boosted this input to 4 W and passed it on to the second amplifier, which we pumped from both ends with a pair of 350-W pump lasers. We put a beamsplitter between the two amplifier stages to monitor not only the input power to the second stage, but the backward-traveling stimulated Brillouin scattering from the second stage as well.
The scattering reflected from the beamsplitter was recorded as a function of the output power of the second amplifier stage (Figure 5). It is clear that the stimulated Brillouin scattering threshold is significantly higher in the specially designed fiber. In the standard large-mode-area fiber, the stimulated Brillouin scattering threshold was approximately 40 W, while the acoustically tailored fiber showed a threshold between 150 and 200 W.
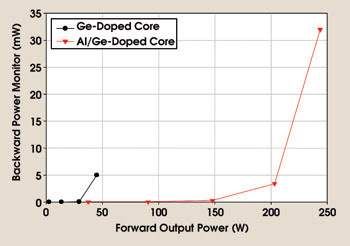
Figure 5. The stimulated Brillouin scattering threshold for standard 30-μm-core, step-index fiber (LMA-1) was ~40 W, compared with 150 to 200 W for the 30-μm-core fiber with the engineered index profile (LMA-2).
This measurement demonstrates the feasibility of raising the stimulated Brillouin scattering threshold through dopant profiling in the core of the fiber. Our current efforts focus on further tailoring our fiber to minimize the overlap between optical and acoustic fields, and to decrease the intensity of the optical fields to approach kilowatt-level, narrow-bandwidth outputs. Two designs of particular interest are:
• Doping the core solely with alumina such that the optical wave sees a typical step index but that the acoustic wave experiences antiguiding because alumina decrease the effective acoustic index with respect to the fiber cladding.
• Adjusting the alumina/germania ratio so that the acoustic index exactly matches that of the cladding and there is no waveguide for the acoustic wave. In this case, the optical wave still sees a step index.
In our preliminary experiments, both cases yielded slight improvements to the stimulated Brillouin scattering properties. We believe that, in the absence of bound longitudinal acoustic waves, the stimulated Brillouin scattering threshold is dictated by evanescent acoustic waves in the fiber cladding.
In the first case, the cladding acoustic modes can become trapped by the depressed acoustic core, analogous to a hollow waveguide. In the latter case, any slight deviations from exact index flatness result in acoustic mode guidance in a low-contrast waveguide or antiguide, depending on the sign of the index step.
Acknowledgment
The author acknowledges the project team for its technical support and DARPA for its financial support.
Meet the author
Donnell Walton is a research associate and manager of the high-power fiber laser program at Corning Inc. in Corning, N.Y.; e-mail: [email protected].