Researchers can use this method to improve clarity — without additional optical hardware — and to obtain access to structures previously hidden above and below the focal plane.
LAUREN ALVARENGA OLYMPUS CORP. OF THE AMERICAS
Deconvolution is a computationally intensive image processing technique used to improve the contrast and sharpness of images captured with a light microscope. Light microscopes are diffraction limited, which means they are unable to resolve individual structures unless they are more than half the wavelength of light away from one another. Each point source below this diffraction limit is blurred by the microscope into what is known as a point spread function (PSF). With traditional wide-field fluorescence microscopy, out-of-focus light from areas above or below the focal plane causes additional blurring in the captured image. This becomes a problem when trying to identify or measure structures inside thicker samples.
Deconvolution reverses this degradation by using the optical system’s PSF and reconstructing an ideal image made from a collection of smaller point sources. This is especially helpful for samples such as spheroids or tissue sections, where areas of interest are often hidden within the sample rather than at the top or bottom, where they can be viewed easily.

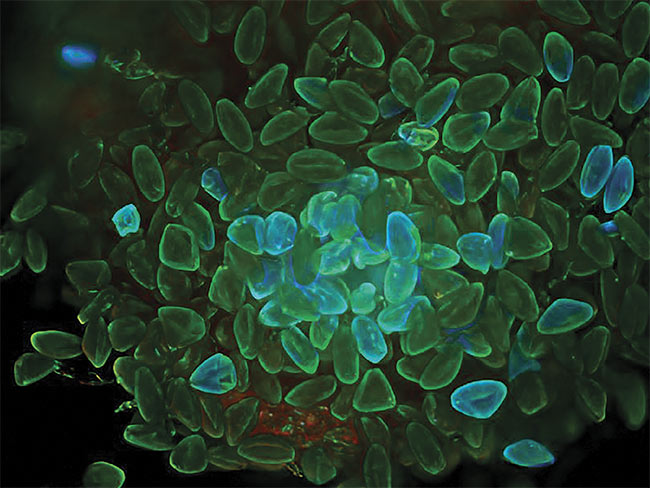
Maximum intensity projections of plant seeds, acquired with a wide-field microscope (top). Deconvolution reverses the degradation with the aid of an
advanced maximum likelihood constrained iterative algorithm (bottom). Courtesy of Joe Dragavon.
A light microscope’s PSF varies based on the optical properties of both the microscope and the sample, making it difficult to experimentally determine the exact optical transformation of the complete system. For this reason, mathematical algorithms have been developed to determine the PSF and to make the best possible reconstruction of the ideal image using deconvolution. Nearly any image acquired with a fluorescence microscope can be deconvolved, including those that are not three-dimensional, meaning that even a single image can benefit from these image processing techniques.
Commercially available software brings these algorithms together into cost-effective, user-friendly packages. Each deconvolution algorithm differs in how the point spread and noise functions of the convolution operations are determined. The basic imaging formula is:
g(x) = f(x) * h(x) + n(x)
where x: spatial coordinate; g(x):
observed image; f(x): object; h(x): PSF; n(x): noise function; *: convolution.
Deblurring algorithms
Deblurring algorithms apply an operation to each two-dimensional plane of
a three-dimensional image stack. A common deblurring technique, “nearest neighbor,” operates on each z-plane by blurring the neighboring planes (z + 1 and z − 1, using a digital blurring filter), then subtracting the blurred planes from the z-plane. Multineighbor techniques extend this concept to a selectable number of planes, allowing users to reduce processing time by eliminating z-planes that are too far out of focus to provide
usable data. A three-dimensional stack
is processed by applying the algorithm
to every selected plane in the stack (figure below).
This class of deblurring algorithms is workable because it involves calculations performed on a small number of image planes. However, there are several disadvantages to these approaches. Structures whose PSFs overlap each other in nearby z-planes may be localized in planes where they do not belong, altering the apparent position of the object when multiple areas of interest are close in proximity to one another. This problem is particularly severe when deblurring a single two-dimensional image because it often contains diffraction rings or light from out-of-focus structures that will then be sharpened as if they were in the correct focal plane.
Inverse filter algorithms
An inverse filter functions by taking the Fourier transform of an image and dividing it by the Fourier transform of the PSF. Division in Fourier space is equivalent to deconvolution in real space, making inverse filtering the simplest method to reverse the convolution in the image and providing the most faithful representation of the image. The calculation is fast, with a similar speed as two-dimensional deblurring methods. However, the method’s utility is limited by noise amplification. During division in Fourier space, small noise variations in the Fourier transform are amplified by the division operation. The result is that blur removal is compromised as a trade-off against a gain in noise. This technique can also introduce an artifact known as ringing, where ghost structures appear surrounding the original object.
Additional noise and ringing can be reduced by plugging in some assumptions about the structure of the object that gave rise to the image. For instance, if the object is assumed to be relatively smooth, noisy solutions with rough edges can be eliminated. Regularization can be applied in one step within an inverse filter, or it can be applied iteratively. The result is an image stripped of high Fourier frequencies, with a smoother appearance. Much of the “roughness” removed in the image resides at Fourier frequencies well beyond the resolution limit and, therefore, the process does not eliminate structures recorded by the microscope. However, because there is a potential for loss of detail, software implementations of inverse filters typically include an adjustable parameter that enables the user to control the trade-off between smoothing and noise amplification for the truest representation of data. In most image-processing software programs, these algorithms have a variety of names, including Wiener deconvolution, regularized least squares, linear least squares, and Tikhonov-Miller regularization.
Constrained iterative algorithms
A typical constrained iterative algorithm improves the performance of inverse filters by applying additional algorithms to restore photons to the correct position in the image. These methods operate in successive cycles based on results from previous cycles, hence the term “iterative.” An initial estimate of the object is performed and convolved with the PSF. The resulting “blurred estimate” is compared with the raw image to compute an error criterion that represents how similar the blurred estimate is to the raw image. Using the information contained in the error criterion, a new iteration takes place. The new estimate is convolved with the PSF, a new error criterion is computed, and so on (figure on previous page). The best estimate is the one that minimizes the error criterion. As the algorithm progresses, each time the software determines that the error criterion has not been minimized, a new estimate is blurred again, and the error criterion is recomputed. The cycle is repeated until the error criterion is minimized or reaches a defined threshold. The final restored image is the object estimate at the last iteration.
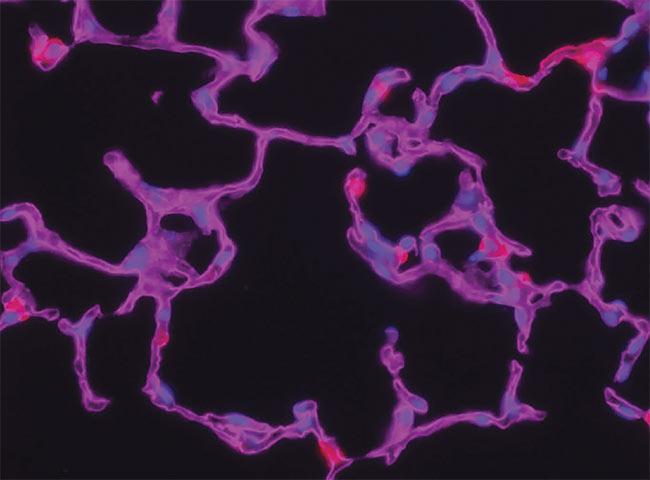
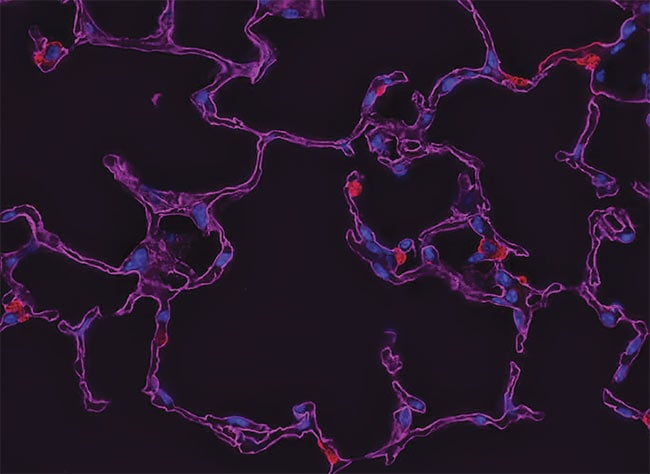
A z-stack for deconvolution, before processing (top) and after (bottom). Courtesy of Gavin Ryan/
Olympus Sales.
The constrained iterative algorithms offer good results, but they are not suitable for all imaging setups. They require long calculation times and place a high demand on computer processors, reducing available processing power for image acquisition or simple data reporting. This can be overcome with modern technol-
ogies, such as GPU-based processing, which significantly improves speed. To take full advantage of the algorithms, three-dimensional images are required, though two-dimensional images can be used with limited performance.
Clarifying microscopic images
Some recommend deconvolution as an alternate technique to using a confocal microscope1. This recommendation is not strictly true because deconvolution techniques can also be applied to the images acquired using the pinhole aperture in a confocal microscope. In fact, it is possible to restore images acquired with a confocal, multiphoton, or superresolution light microscope through convolution.
The combination of optical image improvement through confocal or superresolution microscopy and deconvolution techniques improves sharpness beyond what is generally attainable with either technique alone. However, the major ben-
efit of deconvolving images from these specialized microscopes is decreased noise in the final image. This is particularly helpful for low-light applications
such as live cell superresolution or confocal imaging. Deconvolution of multiphoton images has also been successfully used to remove noise and improve contrast for particularly convoluted images. In all cases, care must be taken to apply an appropriate PSF, especially if the confocal pinhole aperture is adjustable.
Deconvolution in practice
Processing speed and quality are dramatically affected by how software and user controls implement the deconvolution algorithm. The algorithm can be optimized to reduce the number of iterations and accelerate convergence to produce a stable estimate. For example, an unoptimized Jansson-Van Cittert algorithm usually requires between 50 and 100 iterations to converge to an optimal estimate. By prefiltering the raw image to suppress noise and correcting with an additional error criterion on the first two iterations, the algorithm converges in only 5 to 10 iterations.
When using an empirical PSF, it is critical to use a high-quality PSF with minimal noise. To achieve this, commercial software packages contain preprocessing routines that reduce noise and enforce radial symmetry by averaging the Fourier transform of the PSF. Many software packages also enforce axial symmetry in the PSF and assume the absence of spherical aberration. These steps reduce the empirical PSF’s noise and aberrations and make a significant difference in the restoration’s quality.
Preprocessing can also be applied to raw images using routines such as background subtraction and flat-field correction. These operations can improve the signal-to-noise ratio and remove certain artifacts that are detrimental to the final image.
In general, the more faithful the data representation, the more computer memory and processor time are required to deconvolve an image. Previously, images would be divided into subvolumes to accommodate processing power, but modern technologies have reduced this barrier and expanded into larger data sets.
Meet the author
Lauren Alvarenga is a product manager for life science research imaging at Olympus Corp. of the Americas. She is currently responsible for inverted microscopes, imaging software, and superresolution microscopy. Alvarenga received a B.S. in biomedical photographic communications from the Rochester Institute of Technology in 2010.
Reference
1. P.J. Shaw and D.J. Rawlins (1991). The point-spread function of a confocal microscope: its measurement and use in deconvolution of 3-D data. J Microsc, Vol. 163, Issue 2, pp. 151-165.