Nothing has changed the world of communications as much as the development and implementation of optical fiber. This article provides the basic principles needed to work with this technology.
Engineering and Marketing Staff, OFS
Optical fibers are made from either glass or plastic. Most are roughly the diameter of a human hair, and they may be many miles long. Light is transmitted along the center of the fiber from one end to the other, and a signal may be imposed. Fiber optic systems are superior to metallic conductors in many applications. Their greatest advantage is bandwidth. Because of the wavelength of light, it is possible to transmit a signal that contains considerably more information than is possible with a metallic conductor — even a coaxial conductor. Other advantages include:
• Electrical Isolation — Fiber optics do not need a grounding connection. Both the transmitter and the receiver are isolated from each other and are therefore free of ground loop problems. Also, there is no danger of sparks or electrical shock.
• Freedom from EMI — Fiber optics are immune to electromagnetic interference (EMI), and they emit no radiation themselves to cause other interference.
• Low Power Loss — This permits longer cable runs and fewer repeater amplifiers.
• Lighter and Smaller — Fiber weighs less and needs less space than metallic conductors with equivalent signal-carrying capacity.
Copper wire is about 13 times heavier. Fiber also is easier to install and requires less duct space.
Applications
Some of the major application areas of optical fibers are:
• Communications — Voice, data, and video transmission are the most common uses of fiber optics, and these include:
– Telecommunications
– Local area networks (LANs)
– Industrial control systems
– Avionic systems
– Military command, control, and communications systems
• Sensing — Fiber optics can be used to deliver light from a remote source to a detector to obtain pressure, temperature, or spectral information. The fiber also can be used directly as a transducer to measure a number of environmental effects, such as strain, pressure, electrical resistance, and pH. Environmental changes affect the light intensity, phase and/or polarization in ways that can be detected at the other end of the fiber.
• Power Delivery — Optical fibers can deliver remarkably high levels of power for tasks such as laser cutting, welding, marking, and drilling.
• Illumination — A bundle of fibers gathered together with a light source at one end can illuminate areas that are difficult to reach — for example, inside the human body, in conjunction with an endoscope. Also, they can be used as a display sign or simply as decorative illumination.
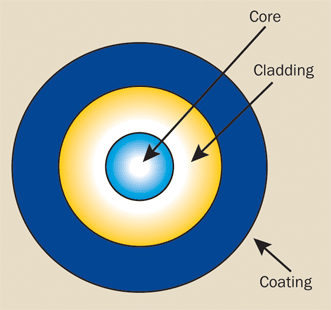
Figure 1. An optical fiber consists of a core, cladding, and coating.
Construction
An optical fiber consists of three basic concentric elements: the core, the cladding, and the outer coating (Figure 1).
The core is usually made of glass or plastic, although other materials are sometimes used, depending on the transmission spectrum desired.
The core is the light-transmitting portion of the fiber. The cladding usually is made of the same material as the core, but with a slightly lower index of refraction (usually about 1% lower). This index difference causes total internal reflection to occur at the index boundary along the length of the fiber so that the light is transmitted down the fiber and does not escape through the sidewalls.
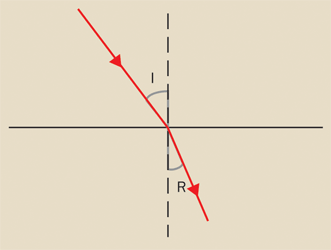
Figure 2. A beam of light passing from one material to another of a different index of refraction is bent or refracted at the interface.
The coating usually comprises one or more coats of a plastic material to
protect the fiber from the physical environment. Sometimes metallic
sheaths are added to the coating for further physical protection.
Optical fibers usually are specified by their size, given as the outer diameter of the core, cladding, and coating. For example, a 62.5/125/250 would refer to a fiber with a 62.5-µm diam core, a 125-µm diam cladding, and a 0.25-mm diam outer coating.
Principles
Optical materials are characterized by their index of refraction, referred to as n. A material’s index of refraction is the ratio
of the speed of light in a vacuum to the speed of light in the material. When a beam of light passes from one material to another with a different index of refraction, the beam is bent (or refracted) at the interface (Figure 2).
Refraction is described by Snell’s law:
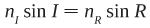
where nI and nR are the indices of refraction of the materials through which the beam is refracted and I and R are the angles of incidence and refraction of the beam. If the angle of incidence is greater than the critical angle for the interface (typically about 82° for optical fibers), the light is reflected back into the incident medium without loss by a process known as total internal reflection (Figure 3).
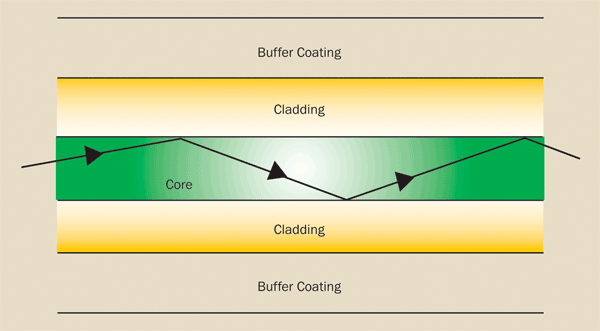
Figure 3. Total internal reflection allows light to remain inside the core of the fiber.
Watch a video definition of total internal reflection.
Modes
When light is guided down a fiber (as microwaves are guided down a waveguide), phase shifts occur at every reflective boundary. There is a finite discrete number of paths down the optical fiber (known as modes) that produce constructive (in phase and therefore additive) phase shifts that reinforce the transmission. Because each mode occurs at a different angle to the fiber axis as the beam travels along the length, each one travels a different length through the fiber from the input to the output. Only one mode, the zero-order mode, travels the length of the fiber without reflections from the sidewalls. This is known as a single-mode fiber. The actual number of modes that can be propagated in a given optical fiber is determined by the wavelength of light and the diameter and index of refraction of the core of the fiber.
Attenuation
Signals lose strength as they are propagated through the fiber; this is known as beam attenuation. Attenuation is measured in decibels (dB) with the relation:
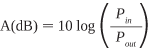
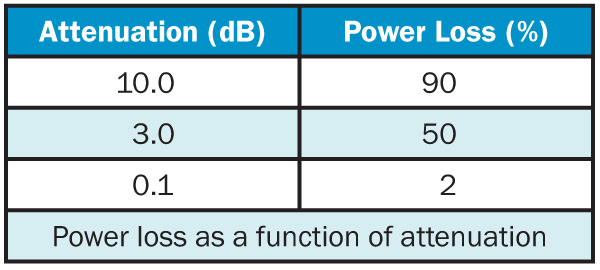
where Pin and Pout refer to the optical power going into and coming out of the fiber. The table below shows the power typically lost in a fiber for several values of attenuation in decibels.
The attenuation of an optical fiber is wavelength dependent. At the extremes of the transmission curve, multiphoton absorption predominates. Attenuation is usually expressed in dB/km at a specific wavelength. Typical values range from 10 dB/km for step-index fibers at 850 nm to a few tenths of a dB/km for single-mode fibers at 1550 nm.
There are several causes of attenuation in an optical fiber:
• Rayleigh Scattering — Microscopic-scale variations in the index of refraction of the core material can cause considerable scatter in the beam, leading to substantial losses of optical power. Rayleigh scattering is wavelength dependent and is less significant at longer wavelengths. This is the most important loss mechanism in modern optical fibers, generally accounting for up to 90% of any loss that is experienced.
• Absorption — Current manufacturing methods have reduced absorption caused by impurities (most notably water in the fiber) to very low levels. Within the bandpass of transmission of the fiber, absorption losses are insignificant.
• Bending — Manufacturing methods can produce minute bends in the fiber geometry. Sometimes these bends will be great enough to cause the light within the core to hit the core/cladding interface at less than the critical angle so that light is lost into the cladding material. This also can occur when the fiber is bent in a tight radius (less than, say, a few centimeters). Bend sensitivity is usually expressed in terms of dB/km loss for a particular bend radius and wavelength.
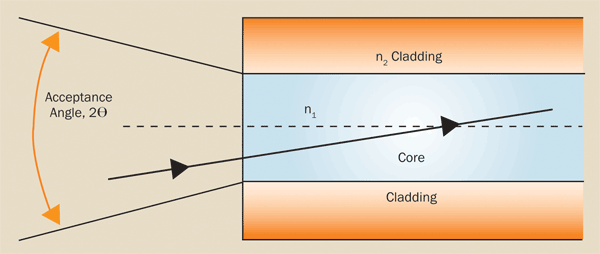
Figure 4. Numerical aperture depends on the angle at which rays enter the fiber and on the diameter of the fiber’s core.
Numerical aperture
Numerical aperture (NA), shown in Figure 4, is the measure of maximum angle at which light rays will enter and be conducted down the fiber. This is represented by the following equation:
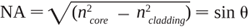
Dispersion
As the optical pulses travel the length of the fiber, they are broadened or lengthened in time. This is called dispersion. Because the pulses eventually will become so out of step that they begin to overlap each other and corrupt the data, dispersion sets an upper limit on the data-carrying capabilities of a fiber. There are three principal causes for this broadening:
• Chromatic Dispersion — Different wavelengths travel at different velocities down the fiber. Because typical light sources provide power over a series or range of wavelengths, rather than from a single discrete spectral line, the pulses must spread out along the length of the fiber as they proceed. The high-speed lasers used in communications have very narrow spectral output specifications, greatly reducing the effect of chromatic dispersion.
• Modal Dispersion — Different fiber modes reflect at different angles as they proceed down the fiber. Because each modal angle produces a somewhat different path length for the beam, the higher-order modes reach the output end of the fiber behind the lower-order modes.
• Waveguide Dispersion — This minor cause for dispersion is due to the geometry of the fiber and results in different propagation velocities for each of the modes.
Bandwidth
Bandwidth measures the data-carrying capacity of an optical fiber and is expressed as the product of the data frequency and the distance traveled (MHz-km or GHz-km, typically). For example, a fiber with a 400-MHz-km bandwidth can transmit 400 MHz for a distance of 1 km, or it can transmit 20 MHz of data for 20 km. The primary limit on bandwidth is pulse broadening, which results from modal and chromatic dispersion of the fiber. Typical values for different types of fiber follow:

Power transmission
The amount of power that a fiber can transmit (without being damaged) is usually expressed in terms of the maximum acceptable power density. Power density is the product of the maximum power output of the laser and the area of the laser beam. For example, a 15-W laser beam focused onto a 150-µm diameter spot produces a power density of
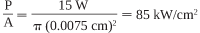
The output of a pulsed laser (typically specified in millijoules of energy per pulse) must first be converted to power per pulse. For example, a pulsed laser that produces 50 mJ in a 10-ns pulse provides an output power of
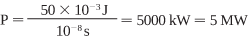
The power density then can be calculated from the spot size.
To transmit the absolute maximum energy levels down a fiber, the fiber end faces must be absolutely smooth and polished and be perpendicular to the fiber axis and the light beam. Also, the beam diameter should be no greater than approximately one-half of the area of the core (or the diameter of the core). If the beam is not appropriately focused, some of the energy may spill into the cladding, which quickly can damage polymer-clad silica fibers. For this reason, it is better to use silica-clad silica fibers in higher power density applications.
Fiber types
There are basically three types of optical fiber: single mode, multimode graded index, and multimode step-index. They are characterized by the way light travels down the fiber and depend on both the wavelength of the light and the mechanical geometry of the fiber. Examples of how they propagate light are shown in Figure 5.
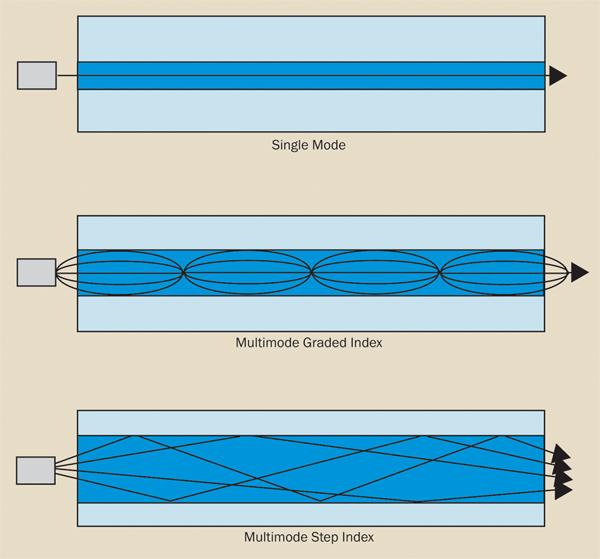
Figure 5. Modes of fiber transmission.
Single mode
Only the fundamental zero-order mode is transmitted in a single-mode fiber. The light beam travels straight through the fiber with no reflections from the core-cladding sidewalls at all. Single-mode fiber is characterized by the wavelength cutoff value, which is dependent on core diameter, NA, and wavelength of operation. Below the cutoff wavelength, higher-order modes may also propagate, which changes the fiber’s characteristics.
Because the single-mode fiber propagates only the fundamental mode, modal dispersion (the primary cause of pulse overlap) is eliminated. Thus, the bandwidth is much higher with a single-mode fiber than that of a multimode fiber. This simply means that pulses can be transmitted much closer together in time without overlap. Because of this higher bandwidth, single-mode fibers are used in all modern long-range communication systems. Typical core diameters are between 5 and 10 µm.
The actual number of modes that can be propagated through a fiber depends on the core diameter, the numerical aperture, and the wavelength of the light being transmitted. These may be combined into the normalized frequency parameter or V number,
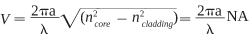
where a is the core radius, λ is the wavelength, and n is the index of the core and the cladding. The condition for single-mode operation is that:
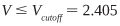
Perhaps more important and useful is the cutoff wavelength. This is the wavelength below which the fiber will allow propagation of multiple modes and can be expressed as:
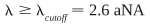
A fiber is typically chosen with a cutoff wavelength slightly below the desired operating wavelength. For lasers typically used as sources (with output wavelengths between 850 and 1550 nm), the core diameter of a single-mode fiber is in the range of 3 to 10 µm.
Multimode graded index
The core diameters of multimode fibers are much larger than single-mode fibers. As a result, higher-order modes also are propagated.
The core in a graded-index fiber has an index of refraction that radially decreases continuously from the center to the cladding interface. As a result, the light travels faster at the edge of the core than in the center. Different modes travel in curved paths with nearly equal travel times. This greatly reduces modal dispersion in the fiber.
As a result, graded-index fibers have bandwidths which are significantly greater than step-index fibers, but still much lower than single-mode fibers. Typical core diameters of graded-index fibers are 50, 62.5, and 100 µm. The main application for graded-index fibers is in medium-range communications, such as local area networks.
Multimode step index
The core of a step-index fiber has a uniform index of refraction right up to the cladding interface where the index changes in a step-like fashion. Because different modes in a step-index fiber travel different path lengths in their journey through the fiber, data transmission distances must be kept short to avoid considerable modal dispersion problems.
Step-index fibers are available with core diameters of 100 to 1500 µm. They are well suited to applications requiring high power densities, such as medical and industrial laser power delivery.