Photonics Rules of Thumb
Scientists and engineers tend to want to answer simple relational questions with a blackboard covered with equations, even when questioners just want a rough estimate to gauge whether a change would cause more problems than it would fix.
The rules of thumb on the following pages provide the framework for this kind of “guesstimate,” with shortcuts to relatively accurate answers. Readers, staff writers, article authors and contributing editors have submitted most of these helpful hints. They are not designed to replace the equations and data sheets that you’ll need to produce commercial or laboratory instruments, systems and components, but to provide a starting point for determining whether a project is feasible.
Fiber Optics
For single-mode fibers, the mode field diameter is roughly 15 percent larger than the core diameter.
The effective return loss (fiber backscatter) of 1 m of single-mode fiber is 69 dB. The equation:

gives an approximate relation of core diameter (d), numerical aperture (NA) and cut-off wavelength (λc) of a single-mode optical fiber.
Detectors
Every 10 °C drop in temperature will reduce silicon PIN photodiode noise by 30 percent.
CCD dark current decreases by half for every 9 °C drop in temperature.
In a photodetector/amplifier system, the amplifier noise increases as the square of the capacitance seen by the amplifier.
Relating an oscilloscope’s bandwidth to the fastest detector rise time it can measure is found by:
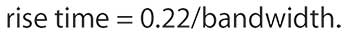
For example, a 100-MHz scope can measure rise times of 2.2 ns.
An optical detector’s responsivity (in amps/watt) is approximately equal to its quantum efficiency divided by 1.24.
In fluorescence lifetime measurement, the ratio of the excitation pulse width to the fluorescence time should be 1:5 to 1:10.
Optics
When an optical coating is shifted from an angle of incidence of 0° to 45°, the wavelength becomes 10 percent shorter. For example, if 0° is at 1064 nm, then 45° is at 958 nm.
For a planoconvex lens, the focal length is twice the radius of the convex surface. This is true for planoconcave lenses as well, but because the surface is reversed, the focal length is negative. For double-concave or double-convex lenses with equal radii, the focal length will equal the radius.
For designing plastic optics:
• Plastics have a low glass transition temperature and high coefficient of thermal expansion, so their use is limited to applications below about 100 °C.
• With long, thin plastic optical components, take into account the effects of the part’s aspect ratio and the effects of gravity that cause deformation over time.
• The optical surface should be larger than the usable clear aperture to accommodate the different thermal characteristics that occur at the edge of the optical insert.
• Mounting features should be uniform along the periphery of the optical surface to prevent nonuniform shrinkage.
• Plastic optics more than 12 mm thick see defects such as flow lines and sinks. Crown glass weighs about 2.5 g/cc or 0.1 lb/in.2 Fused silica is a little less, and flints can be a lot more.
Inserting a glass plate with parallel input and output faces into the air optical path of an imaging system will increase the optical path to the image plane by approximately one-third the thickness of the glass plate.
In almost all applications where spherical aberration is present, the overall image quality is best when the lens is focused to the point of minimum spot size.
The sag of a spherical surface is within 1 percent of y2/(2R) if R/y > 5. R is the radius of curvature of the surface and y is the semi-aperture.
If you are specifying optical coatings and the polarization can be either s or p, it is easier and less costly to reflect s and transmit p.
The commonly used rule of thumb for tolerancing optics is:
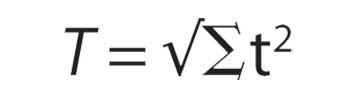
indicating that the probable total effect, T, of a set of additive tolerances is equal to the square root of the sum of the squares of the individual tolerance effects.
Numerical aperture is the cone angle through which an optical system collects or focuses light:

For an optical system with uniform illumination, the minimum focused spot size is:
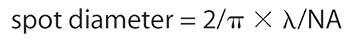
Thus, increasing NA decreases spot size and improves system resolution. However, the depth of focus of an optical system at visible wavelengths is:
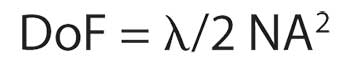
The goal in designing a high-NA lens system is to produce a system in which the lens aperture is nearly as large as the system focal length, while minimizing aberrations.
Linear focus shift (in the visible) is 8 (f number) 2 or 2/(NA) 2 × peak-to-valley OPD. For focus shift, p to v is 3.5 × rms.
For a thin lens working at finite conjugates, the object-to-image distance is (2 −M −(1/ M )) × focal length. M is negative for an inverted image.
To simplify optical alignments, make all adjustments from the same direction; perform manual and nonmanual adjustments identically during a measurement run; adjust only for aberrations (image quality) or alignment (image location); and determine reference points in a system.
Lasers
Light travels about 1 ft/ns. Therefore, to obtain laser ranging accuracy of 5 ft, you must determine the time of flight of reflected light with 5- to 10-ns resolution.
The threshold for retinal damage from an ultrashort-pulse laser (e.g., 100-fs pulses) is five to 10 times lower than for a standard laser.
For semiconductor lasers, the emission wavelength can be approximated by:
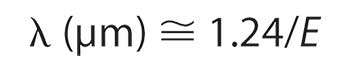
where E is the material bandgap of the active region in electron volts.
Laser beam intensity should be no more than 20 dB above the saturation of a CCD chip to prevent physical damage to the chip.
The coherence length (in meters) of an optical source is determined by:
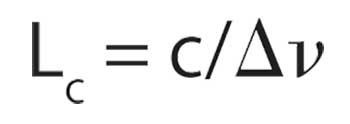
where c is the speed of light in meters per second and Δv is the linewidth of the source in hertz.
In the mid-infrared (8 to 12 μm), the diffraction-limited beamwidth (in milliradians) is approximately equal to the inverse of the optic diameter in inches. Of course, it follows that, in the middle of the visible region at 500 nm, for example, the beamwidth is 1⁄20 as large.
In laser machining, a tenfold increase in laser fluence often raises the overall etch rate by only a factor of three.
The focused spot of a laser beam can be determined by:
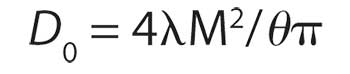
where D0 is the beam’s diameter at the focus of the lens, λ is the wavelength of the laser light, M2 is the beam quality, and θ is the beam divergence.
Imaging
Lens formats for CCD cameras should be larger or the same as the format of the CCD; i.e., a 2 ⁄ 3-in. format lens is OK on a 1 ⁄ 2-in. CCD, but the reverse will cause a porthole effect.
The minimum signal-to-noise ratio for the human eye is about 316:1.
When choosing lighting for machine vision applications, the following principles are useful:
• To gauge simple geometric shapes, directional lighting (especially backlighting) is good.
• To avoid shadows, light should reach a part from several directions.
• Filters can improve color discernment.
• Polarization filters minimize reflections from shiny parts and make their surface appear very dark. Wide-angle, diffused, on-axis light will minimize reflections and make the surface appear very bright.
The minimum linewidth or feature size that can be viewed with the unaided human eye should be roughly 0.003 to 0.005 in. (0.076 to 0.127 mm).
For underwater laser range gated imaging, attenuation length is defined as the 1/e intensity range for a collimated light beam in the water of interest. In inshore turbid waters, increasing range by one attenuation length requires approximately an order of magnitude increase in the product of laser energy × receiver aperture × quantum efficiency.
In choosing the resolution of a camera: The detail under study should cover a minimum of two pixels within the camera’s field of view.
Electro-Optics
Modulation frequency of an acousto-optic device is: Fm × = 0.75
= 0.75
where = D/V;D is the optical beam diameter and V is the sound velocity inside the acousto-optic interaction medium. Fm is the optical intensity modulation frequency where the depth of modulation is −3 dB or 50 percent. At this depth of modulation, the intensity contrast is 3:1.
= D/V;D is the optical beam diameter and V is the sound velocity inside the acousto-optic interaction medium. Fm is the optical intensity modulation frequency where the depth of modulation is −3 dB or 50 percent. At this depth of modulation, the intensity contrast is 3:1. is known as the access time or, in other words, the transit time of an acoustic wavefront across an optical beam of diameter D inside the acousto-optic medium.
is known as the access time or, in other words, the transit time of an acoustic wavefront across an optical beam of diameter D inside the acousto-optic medium.
Optical rise time of an acousto-optic device is: Tr = 0.64 × D/V
where D is the optical diameter and V is the sound velocity inside the acousto-optic interaction medium.
Optical rise time is, by the classical definition, the time it takes for the intensity of an optical pulse to go from the 10 percent to the 90 percent points when a radio frequency step function is applied to the acousto-optic device. This assumes that the device’s electrical bandwidth is wide enough to pass the Fourier pulse components.
Source: Editors and Readers of Photonics Spectra